Gelöste Aufgaben/FEB3: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „d“ |
Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
d | [[Category:Gelöste Aufgaben]] | ||
[[Category:Randwertproblem]] | |||
[[Category:Biege-Belastung]] | |||
[[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Finite-Elemente-Methode]] | |||
[[Category:Geometrische Zwangsbedingung]] | |||
[[Category:Koordinaten]] | |||
[[Category:Maxima]] | |||
[[Category:Statik]] | |||
==Aufgabenstellung== | |||
Hier geht es offensichtlich um Symmetrien, die wir mit einer skalaren Gleichgewichtsformulierung wie dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] sehr elegant ausnutzen können. | |||
Die Euler-Bernoulli-Balken ''AB'' und ''CD'' (Länge ''2ℓ'', Biegesteifigkeit ''EI'') sind in ''A'' und ''B'' bzw. ''C'' und ''D'' gelenkig gelagert. Jeweils mittig haben die beiden Balken einen Verbindungspunkt, in die eine Feder der Steifigkeit ''k'' eingehängt wird. Zum Einhängen muss bei entspannten Balken die Feder um die Länge ''d'' gelängt werden. Nach dem Loslassen stellt sich dann eine neue statische Gleichgewichtslage zwischen Balken und Feder ein. | |||
<onlyinclude>[[Datei:FEB3-01.png|mini|left|Lageplan.|alternativtext=|200x200px]]Gesucht sind die Auslenkungen der beiden Verbindungspunkte der Feder mit den Balken. Das Modell soll aus vier Finiten Elementen bestehen, jeweils zwei für die beiden Balken sowie einer Feder. | |||
</onlyinclude> | |||
== Lösung mit Maxima == | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | |||
|text= | |||
Hier müssen die Element-Steifigkeitsmatrizen für vier Sektionen von [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] und einer Feder zusammengefügt (assembliert) werden. Die Schwierigkeit liegt darin, die Symmetrien des Systems auszunutzen. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 16.04.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-12-23 */ | |||
/* ref: TM-C */ | |||
/* description: FEM-solution for two beams, centrally */ | |||
/* connected by a spring */ | |||
/*******************************************************/ | |||
/* declare variational variables - see 6.3 Identifiers */ | |||
declare("δW", alphabetic); | |||
declare("δA", alphabetic); | |||
declare("δΠ", alphabetic); | |||
declare("δw", alphabetic); | |||
declare("δQ", alphabetic); | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | |||
|text= | |||
Wir kopieren den Ausdruck für die virtuelle Formänderungsenergie aus der FEM-Formulierung für den Euler-Bernoulli-Balken für Element "''i''" zu | |||
::<math>\delta\Pi_i = \delta\underline{Q}^T \cdot \underline{\underline{K}}_i \cdot \underline{Q}</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/***************************************************/ | |||
/* FEM-Formulierung+für+den+Euler-Bernoulli-Balken */ | |||
/*Trial-Fucntions*/ | |||
Ki(l):= (EI/l^3)*matrix([ 12, 6*l ,-12 , 6*l ], | |||
[6*l, 4*l^2, -6*l, 2*l^2], | |||
[-12,-6*l , 12 ,-6*l ], | |||
[6*l, 2*l^2, -6*l, 4*l^2]); | |||
/***************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
Der Schlüssel zur einfachen Lösung liegt in der Symmetrie der Verformung des Systems: alle vier Balken-Elemente verformen sich gleich. So verformt sich der Balken ''AB'' symmetrisch zum mittleren Verbindungspunkt "M", das gleiche gilt für Balken CD. | |||
Für das Finite Element ''AM'' sind nun die Knotenvariablen | |||
::<math>\underline{Q}_{AM} = \left(\begin{array}{l}W_A\\\Phi_A\\W_M\\\Phi_M\end{array}\right)</math>, | |||
wobei wegen der Rand- und Übergangsbedingungen | |||
::<math>\begin{array}{l}W_A = 0 \text{ und }\\ \Phi_M = 0\end{array}</math> | |||
gilt. Nach Einarbeiten dieser Bedingungen ist also die virtuelle Formänderungsenergie des Balken-Segments | |||
::<math>\displaystyle \delta\Pi_{AM} = \left(\delta \Phi_A, \delta W_M\right)\cdot \frac{EI}{\ell^3} \left(\begin{array}{cc}4\ell^2&-6\ell\\-6\ell&12 \end{array}\right) \cdot \left(\begin{array}{l}\Phi_A\\ W_M\end{array}\right)</math>. | |||
Analog ist die virtuelle Formänderungsenergie der Feder | |||
::<math>\delta\Pi_k = k\cdot (d-2\;W_M)\cdot(-2\;\delta W_M)</math> | |||
weil unterer und oberer Verbindungspunkt gleich ausgelenkt werden - wenn auch mit unterschiedlichen Orientierungen. | |||
Wir haben keine eingeprägten, äußeren Kräfte - also gilt im Gleichgewicht | |||
::<math>\delta\Pi = 0</math>. | |||
Nun ist | |||
::<math>\displaystyle \delta\Pi = \underbrace{\sum^4_{I=1} \delta\Pi_i}_{\displaystyle = 4\;\delta\Pi_{AM}} + \delta\Pi_k</math> | |||
und damit folgt die Gleichgewichtsbedingung zu | |||
::<math>\begin{pmatrix}\displaystyle \frac{16\cdot \mathit{EI}}{l} &\displaystyle -\frac{24\cdot \mathit{EI}}{{{l}^{2}}}\\ \displaystyle -\frac{24\cdot \mathit{EI}}{{{l}^{2}}} &\displaystyle \frac{48\cdot \mathit{EI}}{{{l}^{3}}}+4\cdot k\end{pmatrix}\cdot \begin{pmatrix}{{\Phi}_{A}}\\{{W}_{M}}\end{pmatrix}=\begin{pmatrix}0\\ 2\; d\; k\end{pmatrix}</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/***************************************************/ | |||
/* virtuelle Formänderungsenergie der Feder */ | |||
Q : matrix([Phi[A]],[W[M]]); | |||
δΠ[k] : k*(d-2*W[M])*(-2*δW[M]); | |||
/* Gesamt-Matrizen */ | |||
K : 4* submatrix(1,4,Ki(l),1,4) | |||
K[2,2] : K[2,2] + coeff(coeff(expand(δΠ[k]),δW[M]),W[M]); | |||
P : matrix([0],[-subst(0,W[M],coeff(expand(δΠ[k]),δW[M]))]) | |||
print(K,"*",Q,"=",P); | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | |||
|text= | |||
Lösen des Gleichungssystems liefert | |||
::<math>\begin{array}{l}\displaystyle \Phi_A = \frac{3\; d\; k\; \ell^{2}}{12\; EI+4\; k\; \ell^{3}}\\\displaystyle W_M=\frac{d\; k\; \ell^3}{6\; EI+2\; k\; \ell^3}\end{array}</math>, | |||
und das ist zum Beispiel für ''k = EI / ℓ<sup>3</sup>'' | |||
::<math>\begin{array}{l}\displaystyle \Phi_A = \frac{3\; d}{16\; \ell}\\\displaystyle W_M = \frac{d}{8}\end{array}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/***************************************************/ | |||
/* solve */ | |||
sol : ratsimp(linsolve_by_lu(K,P)); | |||
subst([k=EI/l^3],sol); | |||
</syntaxhighlight> | |||
}} | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 26. Oktober 2022, 07:12 Uhr
Aufgabenstellung
Hier geht es offensichtlich um Symmetrien, die wir mit einer skalaren Gleichgewichtsformulierung wie dem Prinzip der virtuellen Verrückungen sehr elegant ausnutzen können.
Die Euler-Bernoulli-Balken AB und CD (Länge 2ℓ, Biegesteifigkeit EI) sind in A und B bzw. C und D gelenkig gelagert. Jeweils mittig haben die beiden Balken einen Verbindungspunkt, in die eine Feder der Steifigkeit k eingehängt wird. Zum Einhängen muss bei entspannten Balken die Feder um die Länge d gelängt werden. Nach dem Loslassen stellt sich dann eine neue statische Gleichgewichtslage zwischen Balken und Feder ein.
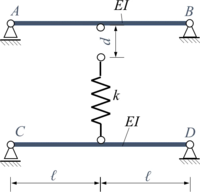
Gesucht sind die Auslenkungen der beiden Verbindungspunkte der Feder mit den Balken. Das Modell soll aus vier Finiten Elementen bestehen, jeweils zwei für die beiden Balken sowie einer Feder.
Lösung mit Maxima
Header
Hier müssen die Element-Steifigkeitsmatrizen für vier Sektionen von Euler-Bernoulli-Balken und einer Feder zusammengefügt (assembliert) werden. Die Schwierigkeit liegt darin, die Symmetrien des Systems auszunutzen.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-12-23 */
/* ref: TM-C */
/* description: FEM-solution for two beams, centrally */
/* connected by a spring */
/*******************************************************/
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δA", alphabetic);
declare("δΠ", alphabetic);
declare("δw", alphabetic);
declare("δQ", alphabetic);
Declarations
Wir kopieren den Ausdruck für die virtuelle Formänderungsenergie aus der FEM-Formulierung für den Euler-Bernoulli-Balken für Element "i" zu
- .
/***************************************************/
/* FEM-Formulierung+für+den+Euler-Bernoulli-Balken */
/*Trial-Fucntions*/
Ki(l):= (EI/l^3)*matrix([ 12, 6*l ,-12 , 6*l ],
[6*l, 4*l^2, -6*l, 2*l^2],
[-12,-6*l , 12 ,-6*l ],
[6*l, 2*l^2, -6*l, 4*l^2]);
/***************************************************/
Equilibrium Conditions
Der Schlüssel zur einfachen Lösung liegt in der Symmetrie der Verformung des Systems: alle vier Balken-Elemente verformen sich gleich. So verformt sich der Balken AB symmetrisch zum mittleren Verbindungspunkt "M", das gleiche gilt für Balken CD.
Für das Finite Element AM sind nun die Knotenvariablen
- ,
wobei wegen der Rand- und Übergangsbedingungen
gilt. Nach Einarbeiten dieser Bedingungen ist also die virtuelle Formänderungsenergie des Balken-Segments
- .
Analog ist die virtuelle Formänderungsenergie der Feder
weil unterer und oberer Verbindungspunkt gleich ausgelenkt werden - wenn auch mit unterschiedlichen Orientierungen.
Wir haben keine eingeprägten, äußeren Kräfte - also gilt im Gleichgewicht
- .
Nun ist
und damit folgt die Gleichgewichtsbedingung zu
- .
/***************************************************/
/* virtuelle Formänderungsenergie der Feder */
Q : matrix([Phi[A]],[W[M]]);
δΠ[k] : k*(d-2*W[M])*(-2*δW[M]);
/* Gesamt-Matrizen */
K : 4* submatrix(1,4,Ki(l),1,4)
K[2,2] : K[2,2] + coeff(coeff(expand(δΠ[k]),δW[M]),W[M]);
P : matrix([0],[-subst(0,W[M],coeff(expand(δΠ[k]),δW[M]))])
print(K,"*",Q,"=",P);
Solving
Lösen des Gleichungssystems liefert
- ,
und das ist zum Beispiel für k = EI / ℓ3
/***************************************************/
/* solve */
sol : ratsimp(linsolve_by_lu(K,P));
subst([k=EI/l^3],sol);
Links
- ...
Literature
- ...