Gelöste Aufgaben/FEC1/FEC1 - Teil III: Simulieren: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (17 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
Um unsere Bewegungsgleichungen | Um unsere Bewegungsgleichungen | ||
::<math>\ | ::<math> | ||
\underline{\underline{M}}\;\underline{\ddot{Q}} + \underline{\underline{G}}\; \underline{\dot{Q}} + \left( \underline{\underline{K}}_C \cos(2\Omega t)+\underline{\underline{K}}_S \sin(2 \Omega t)+\underline{\underline{K}}_D+\underline{\underline{K}}_0\right)\; \underline{Q} = \underline{P} | |||
</math> | |||
zu lösen, war der Computer und [[Werkzeuge/Software/Maxima|Maxima]] bis hierher eine gute Hilfe - wir hätten aber auch alle Gleichungen per Hand aufstellen können. Ab hier geht das nicht mehr. Für die Lösung der Bewegungsgleichungen brauchen wir Computer. Für einfache Probleme wie dieses reichen Interpreter-Programme wie [[Werkzeuge/Software/Matlab|Matlab]]©, wenn's komplizierter wird, müssten wir auf Kompiler wie C++ umsteigen. Für alle etablierten Programme gibt es Numerik-Bibliotheken, um die Probleme zu lösen, die wir jetzt angehen. | zu lösen, war der Computer und [[Werkzeuge/Software/Maxima|Maxima]] bis hierher eine gute Hilfe - wir hätten aber auch alle Gleichungen per Hand aufstellen können. Ab hier geht das nicht mehr. Für die Lösung der Bewegungsgleichungen brauchen wir Computer. Für einfache Probleme wie dieses reichen Interpreter-Programme wie [[Werkzeuge/Software/Matlab|Matlab]]©, wenn's komplizierter wird, müssten wir auf Kompiler wie C++ umsteigen. Für alle etablierten Programme gibt es Numerik-Bibliotheken, um die Probleme zu lösen, die wir jetzt angehen. | ||
| Zeile 11: | Zeile 13: | ||
Bei allen Lösungsansätzen steht in der Bewegungsgleichung noch ein Parameter: die Dimensionslose Drehzahl η mit | Bei allen Lösungsansätzen steht in der Bewegungsgleichung noch ein Parameter: die Dimensionslose Drehzahl η mit | ||
::<math>\displaystyle \Omega = \eta \cdot \omega_{0,0} \text{ und der Eigenfrequenz } \omega_{0,0}^2 = 3 \frac{E I}{\ell^3 m_I}</math> | |||
{{ | {{MyNoncodeBlock|title=Partikulare Lösung für konstante Koeffizienten | ||
|text= | |text= | ||
Für die Bewegungsgleichung oben gibt es keine geschlossene partikulare Lösung - die periodischen Koeffizienten machen das unmöglich. Anschaulich berücksichtigen diese Koeffizienten die Drehwinkel-veränderliche Steifigkeit der Lager beim Drehen. | |||
Wir könnten von ''Δk = 0'' ausgehen und die Lösung von | |||
::<math>\underline{\underline{K}}_0\; \underline{Q}_P = \underline{P}</math> | |||
berechnen. Aber hier steht nichts, was wir nicht mit einer Handrechnung auch hinbekommen würden: die Auslenkung des Systems wächst quadratisch mit der Drehzahl ''η(Ω)'' - also der Zentrifugalkraft. | |||
}} | |||
==Lösung== | |||
<!-- ---------------------------------------------------------------------------- --> | |||
{{MyCodeBlock | |||
|title=Homogene Lösung für konstante Koeffizienten | |||
|text=Auch für die homogene, lineare Differentialgleichung (für ''P''=''0'') gibt es keine geschlossene analytische Lösung. Wir schauen und also auch hier erst einmal nach einer Lösung der homogenen Differentialgleichung mit konstanten Koeffizienten | |||
::<math>\underline{\underline{M}}\;\underline{\ddot{Q}} + \underline{\underline{G}}\; \underline{\dot{Q}} + \underline{\underline{K}}_0\; \underline{Q} = \underline{0}</math> | |||
um und führen wir eine [[Sources/Lexikon/Modalanalyse|Modalanalyse]] durch. Damit wir mit Standard-Lösungsroutinen arbeiten können, transformieren wir die Bewegungsgleichung in eine Differentialgleichung erster Ordnung, hier | |||
::<math>\left(\begin{array}{c}\underline{\dot{P}}\\ \underline{\dot{Q}}\end{array}\right) = \left(\begin{array}{cc}-\underline{\underline{M}}^{-1}\cdot \underline{\underline{G}}&-\underline{\underline{M}}^{-1}\cdot \underline{\underline{K}}\\\underline{\underline{1}}&\underline{\underline{0}}\end{array}\right)\cdot \left(\begin{array}{c}\underline{P}\\\underline{Q}\end{array}\right)</math>. | |||
Dabei ist ''<u>P</u> = d<u>Q</u>/dτ'', also die Geschwindigkeit von Auslenkung und Kippung. Wir haben also nun eine neue Schreibweise für die homogene Differentialgleichung als | |||
::<math>\underline{\dot{X}} = \underline{\underline{H}}(\eta)\cdot \underline{X}</math> | |||
mit | |||
::<math>\underline{X} = \left(\begin{array}{c}\underline{P}\\\underline{Q}\end{array}\right) \text{ und } \underline{P} = \underline{\dot{Q}}</math>. | |||
Für dieses Standard-Problem können wir in [[Werkzeuge/Software/Maxima|Maxima]] eine Adaption der [https://de.wikipedia.org/wiki/LAPACK Lapack-Routinen] nutzen. | |||
|code= | |code= | ||
< | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/******************* PART III **************************/ | |||
/*******************************************************/ | |||
/* rewrite as first-order differential equations */ | |||
/* X' = H(τ)*X + R, X = (P,Q)^T, R = (0,P)^T */ | |||
/* inverse of M */ | |||
I: dgesv (mats[1], diagmatrix (8, 1))$ | |||
/* System Matrix */ | |||
H : zeromatrix(2*8,2*8)$ | |||
/* G*M^(-1) */ | |||
GI : expand(mats[2].I)$ | |||
/* populate system matrix */ | |||
for row:1 thru 8 do | |||
for col:1 thru 8 do | |||
(H[ row,8+col] : + I [row,col], | |||
H[8+row, col] : -mats[3][row,col], | |||
H[8+row,8+col] : -GI [row,col])$ | |||
/*******************************************************/ | |||
/* solve eigenvalue Problem */ | |||
evals: []$ | |||
for Eta:0 thru 30 step 0.1 do | |||
(/*print("eta = ", Eta),*/ | |||
evals: append(evals, [append([Eta], dgeev (subst([eta = Eta],H))[1])]))$ | |||
etas : flatten(makelist(makelist(evals[i][1],j,1,length(evals[i])-1),i,1,length(evals)))$ | |||
reals: flatten(makelist(makelist(realpart(evals[i][j]),j,2,length(evals[i])),i,1,length(evals)))$ | |||
imags: flatten(makelist(makelist(imagpart(evals[i][j]),j,2,length(evals[i])),i,1,length(evals)))$ | |||
plot2d([[discrete, etas, reals],[discrete, etas, imags]], [y,-100,100], | |||
[style,points,points], [point_type,bullet,plus], | |||
[color,red, blue], [legend, "real part", "imag part"], | |||
[xlabel, "η->"], [ylabel, "ω, γ ->"], | |||
[gnuplot_term, "png size 2000,2000 font 'Helvetica,30'"], [gnuplot_out_file, "C:\\Users\\abs384\\OneDrive\\X\\tmp\\plots\\eigenvalues.png"] )$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
==Lösung berechnen und ausdeuten== | |||
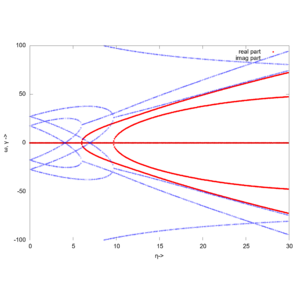
Wir schauen uns die Eigenwerte des Systems für die Drehzahl ''η'' im Bereich 0 < ''η < 30'' an. Für unsere Bewegungsgleichung erster Ordnung mit 16 Zustandsgrößen erhalten wir 16 Eigenwerte mit Real- und Imaginärteil. Die Lösung im Zeitbereich ist dann | |||
::<math>\displaystyle \underline{X}(t) = \sum_{i=1}^{16} \underline{\hat{X}}_i \cdot e^{\displaystyle \gamma_i t + j \omega_{0,i} t}</math> | |||
[[Datei:FEC1-Eigenvalues.png|mini|Eigenwerte als Funktion der Drehzahl ''η''.]] | |||
Wir berechnen die Eigenwerte des Systems nach | |||
= | * <span style="color:#f00000">'''Realteil ''γ'''''</span><br/> und | ||
* <span style="color:#0000f0">'''Imaginärteil ''ω<sub>0,i</sub>''.'''</span> | |||
Für dynamische Instabilität des Systems suchen wir nach Lösungen mit einem Realteil ''γ'' > 0. | |||
<ul> | |||
<li>'''0 < ''η < 6.1'''''<br/> | |||
Für ''η=0'' (die Welle rotiert nicht) sehen wir, dass alle Eigenwerte doppelt auftreten - wir haben 2*8 Eigenwerte. Das kennen wir bereits aus Modalanalysen für andere nicht-rotierende Systeme. | |||
Steigern wir die Drehzahl, so teilen sich die Eigenfrequenzen und wir sehen wirklich 16 unterschiedliche Eigenwerte. Auch diese unterscheiden sich jeweils paarweise nur durch das Vorzeichen. | |||
</li> | |||
<li>'''''η = 6.1'''''<br/> | |||
Bei dieser Drehzahl verzweigt der Realteil der Lösung - ein Lösungszweig (branch) hat einen negativen Realteil, der zu einer abklingenden Lösung gehört und ein zweiter Lösungszweig hat einen positiven Realteil, der zu einer aufklingenden Lösung gehört.<br/> | |||
[[Datei:FEC1-Eigenvalues-Ausschnitt-1.png|rahmenlos|150x150px]] | |||
</li> | |||
<li>'''''η > 6.1'''''<br/> | |||
Für ''η > 6.1'' existieren immer aufklingende Lösungen - die Energie der Drehbewegung führt zur Anfachung der Bewegung im Zeitbereich. | |||
==Rechenergebnisse mit beobachtetem Verhalten des Systems vergleichen== | ==Rechenergebnisse mit beobachtetem Verhalten des Systems vergleichen== | ||
Und hier würden wir die gefundenen Ergebnisse mit Experimenten vergleichen. | |||
Experimente fehlen uns aber leider ... | |||
Aktuelle Version vom 8. Juni 2022, 12:52 Uhr
Computerprogramm schreiben
Um unsere Bewegungsgleichungen
zu lösen, war der Computer und Maxima bis hierher eine gute Hilfe - wir hätten aber auch alle Gleichungen per Hand aufstellen können. Ab hier geht das nicht mehr. Für die Lösung der Bewegungsgleichungen brauchen wir Computer. Für einfache Probleme wie dieses reichen Interpreter-Programme wie Matlab©, wenn's komplizierter wird, müssten wir auf Kompiler wie C++ umsteigen. Für alle etablierten Programme gibt es Numerik-Bibliotheken, um die Probleme zu lösen, die wir jetzt angehen.
Bei allen Lösungsansätzen steht in der Bewegungsgleichung noch ein Parameter: die Dimensionslose Drehzahl η mit
Partikulare Lösung für konstante Koeffizienten
Für die Bewegungsgleichung oben gibt es keine geschlossene partikulare Lösung - die periodischen Koeffizienten machen das unmöglich. Anschaulich berücksichtigen diese Koeffizienten die Drehwinkel-veränderliche Steifigkeit der Lager beim Drehen.
Wir könnten von Δk = 0 ausgehen und die Lösung von
berechnen. Aber hier steht nichts, was wir nicht mit einer Handrechnung auch hinbekommen würden: die Auslenkung des Systems wächst quadratisch mit der Drehzahl η(Ω) - also der Zentrifugalkraft.
Lösung
Homogene Lösung für konstante Koeffizienten
Auch für die homogene, lineare Differentialgleichung (für P=0) gibt es keine geschlossene analytische Lösung. Wir schauen und also auch hier erst einmal nach einer Lösung der homogenen Differentialgleichung mit konstanten Koeffizienten
um und führen wir eine Modalanalyse durch. Damit wir mit Standard-Lösungsroutinen arbeiten können, transformieren wir die Bewegungsgleichung in eine Differentialgleichung erster Ordnung, hier
- .
Dabei ist P = dQ/dτ, also die Geschwindigkeit von Auslenkung und Kippung. Wir haben also nun eine neue Schreibweise für die homogene Differentialgleichung als
mit
- .
Für dieses Standard-Problem können wir in Maxima eine Adaption der Lapack-Routinen nutzen.
/*******************************************************/
/******************* PART III **************************/
/*******************************************************/
/* rewrite as first-order differential equations */
/* X' = H(τ)*X + R, X = (P,Q)^T, R = (0,P)^T */
/* inverse of M */
I: dgesv (mats[1], diagmatrix (8, 1))$
/* System Matrix */
H : zeromatrix(2*8,2*8)$
/* G*M^(-1) */
GI : expand(mats[2].I)$
/* populate system matrix */
for row:1 thru 8 do
for col:1 thru 8 do
(H[ row,8+col] : + I [row,col],
H[8+row, col] : -mats[3][row,col],
H[8+row,8+col] : -GI [row,col])$
/*******************************************************/
/* solve eigenvalue Problem */
evals: []$
for Eta:0 thru 30 step 0.1 do
(/*print("eta = ", Eta),*/
evals: append(evals, [append([Eta], dgeev (subst([eta = Eta],H))[1])]))$
etas : flatten(makelist(makelist(evals[i][1],j,1,length(evals[i])-1),i,1,length(evals)))$
reals: flatten(makelist(makelist(realpart(evals[i][j]),j,2,length(evals[i])),i,1,length(evals)))$
imags: flatten(makelist(makelist(imagpart(evals[i][j]),j,2,length(evals[i])),i,1,length(evals)))$
plot2d([[discrete, etas, reals],[discrete, etas, imags]], [y,-100,100],
[style,points,points], [point_type,bullet,plus],
[color,red, blue], [legend, "real part", "imag part"],
[xlabel, "η->"], [ylabel, "ω, γ ->"],
[gnuplot_term, "png size 2000,2000 font 'Helvetica,30'"], [gnuplot_out_file, "C:\\Users\\abs384\\OneDrive\\X\\tmp\\plots\\eigenvalues.png"] )$
Lösung berechnen und ausdeuten
Wir schauen uns die Eigenwerte des Systems für die Drehzahl η im Bereich 0 < η < 30 an. Für unsere Bewegungsgleichung erster Ordnung mit 16 Zustandsgrößen erhalten wir 16 Eigenwerte mit Real- und Imaginärteil. Die Lösung im Zeitbereich ist dann
Wir berechnen die Eigenwerte des Systems nach
- Realteil γ
und - Imaginärteil ω0,i.
Für dynamische Instabilität des Systems suchen wir nach Lösungen mit einem Realteil γ > 0.
- 0 < η < 6.1
Für η=0 (die Welle rotiert nicht) sehen wir, dass alle Eigenwerte doppelt auftreten - wir haben 2*8 Eigenwerte. Das kennen wir bereits aus Modalanalysen für andere nicht-rotierende Systeme. Steigern wir die Drehzahl, so teilen sich die Eigenfrequenzen und wir sehen wirklich 16 unterschiedliche Eigenwerte. Auch diese unterscheiden sich jeweils paarweise nur durch das Vorzeichen. - η = 6.1
Bei dieser Drehzahl verzweigt der Realteil der Lösung - ein Lösungszweig (branch) hat einen negativen Realteil, der zu einer abklingenden Lösung gehört und ein zweiter Lösungszweig hat einen positiven Realteil, der zu einer aufklingenden Lösung gehört.

- η > 6.1
Für η > 6.1 existieren immer aufklingende Lösungen - die Energie der Drehbewegung führt zur Anfachung der Bewegung im Zeitbereich.Rechenergebnisse mit beobachtetem Verhalten des Systems vergleichen
Und hier würden wir die gefundenen Ergebnisse mit Experimenten vergleichen.
Experimente fehlen uns aber leider ...