Sources/Lexikon/Kugelkoordinaten: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
Die Kugelkoordinaten kann man - ähnlich wie bei den [[Sources/Lexikon/Eulersche_Winkel|Euler-Winkeln]] -zur Definition eines neuen, lokalen Koordinatensystems nutzen. | Die Kugelkoordinaten kann man - ähnlich wie bei den [[Sources/Lexikon/Eulersche_Winkel|Euler-Winkeln]] -zur Definition eines neuen, lokalen Koordinatensystems nutzen. | ||
Mit dem Flächen-Normalenvektor <math>\vec{e}_r</math> und den Tangentialvektoren <math>\vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}</math> zu ''φ<sub>1</sub>'' und ''φ<sub>2</sub>'' wird dabei eine neue Basis <math>\vec{\underline{e}}_K</math> aufgespannt. | |||
[[Datei:Kugelkoordinaten-02.png|210px|right|mini|Einheitsvektoren der Orthogonalbasis <math>\vec{\underline{e}}_K = \left[\vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}, \vec{e}_r\right]</math>, die in Punkt ''P'' der Kugel mit <math>\vec{e}_r</math> die Flächennormale definieren und mit <math>\vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}</math> die Tangentialebene aufspannen.]] | [[Datei:Kugelkoordinaten-02.png|210px|right|mini|Einheitsvektoren der Orthogonalbasis <math>\vec{\underline{e}}_K = \left[\vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}, \vec{e}_r\right]</math>, die in Punkt ''P'' der Kugel mit <math>\vec{e}_r</math> die Flächennormale definieren und mit <math>\vec{e}_{\varphi,1}, \vec{e}_{\varphi,2}</math> die Tangentialebene aufspannen.]] | ||
Die Koordinatentransformation erfolgt über | Die Koordinatentransformation erfolgt über | ||
| Zeile 36: | Zeile 36: | ||
::<math>\underline{\underline{D}}^K_{[1/2,3]}(\theta_1,\theta_2,\theta_3) = \underline{\underline{D}}_{3}(\theta_3)\cdot\underline{\underline{D}}_{12}(\theta_1,\theta_2) | ::<math>\underline{\underline{D}}^K_{[1/2,3]}(\theta_1,\theta_2,\theta_3) = \underline{\underline{D}}_{3}(\theta_3)\cdot\underline{\underline{D}}_{12}(\theta_1,\theta_2) | ||
</math> | </math> | ||
mit den Winkeln ''θ<sub>1</sub>, θ<sub>2</sub>, θ<sub>3</sub>'' | mit den Winkeln ''θ<sub>1</sub>, θ<sub>2</sub>, θ<sub>3</sub>''. | ||
Damit ein beliebiger Punkt nach beiden Transformationen gleich ist, muss | |||
::<math> | |||
\left(a_x, a_y, a_z\right)\cdot\underline{\underline{D}}^E_{[2,1,3]}(\varphi_1,\varphi_2,\varphi_3) = | |||
\left(a_x, a_y, a_z\right)\cdot\underline{\underline{D}}^K_{[1/2,3]}(\theta_1,\theta_2,\theta_3) | |||
</math> | |||
gelten. Diese Beziehungen kann man sukzessive nach den sin- und cos-Koeffizienten auflösen. Sie liefern | |||
::<math> | ::<math> | ||
\begin{array}{lcl}\ | \begin{array}{lcl} | ||
\ | {{\sin{\left( {{\theta }_3}\right) }}^2}&=&\displaystyle \frac{{{\sin{\left( {{\varphi }_2}\right) }}^{2}} {{\sin{\left( {{\varphi }_3}\right) }}^{2}}+2 \sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } \sin{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) } \sin{\left( {{\varphi }_3}\right) }+\left( 1-{{\cos{\left( {{\varphi }_1}\right) }}^{2}}\right) {{\cos{\left( {{\varphi }_2}\right) }}^{2}} {{\cos{\left( {{\varphi }_3}\right) }}^{2}}}{1-{{\cos{\left( {{\varphi }_1}\right) }}^{2}} {{\cos{\left( {{\varphi }_2}\right) }}^{2}}}\\ | ||
\cos{\left( {{\theta }_3}\right) }&=&\displaystyle \frac{\sin{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) } \sin{\left( {{\varphi }_3}\right) }+\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } {{\cos{\left( {{\varphi }_3}\right) }}^{2}}-\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } {{\sin{\left( {{\theta }_3}\right) }}^{2}}}{\sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\theta }_3}\right) }}\\ | |||
\sin{\left( {{\theta } | \sin{\left( {{\theta }_2}\right) }&=&\displaystyle -\frac{\sin{\left( {{\varphi }_1}\right) } \sin{\left( {{\theta }_3}\right) }}{\sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\varphi }_3}\right) }+\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) }}\\ | ||
\cos{\left( {{\theta } | \cos{\left( {{\theta }_2}\right) }&=&\displaystyle \frac{\cos{\left( {{\varphi }_1}\right) } \sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\theta }_3}\right) }}{\sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\varphi }_3}\right) }+\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) }}\\ | ||
\sin{\left( {{\theta }_1}\right) }&=&\displaystyle \frac{\sin{\left( {{\varphi }_2}\right) } \sin{\left( {{\varphi }_3}\right) }+\sin{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) } \cos{\left( {{\varphi }_3}\right) }}{\sin{\left( {{\theta }_3}\right) }}\\ | |||
\cos{\left( {{\theta }_1}\right) }&=\displaystyle &\cos{\left( {{\varphi }_1}\right) } \cos{\left( {{\varphi }_2}\right) }\\ | |||
\end{array} | |||
</math> | </math> | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
Aktuelle Version vom 4. April 2022, 13:38 Uhr
In Kugelkoordinaten oder räumlichen Polarkoordinaten wird ein Punkt P im dreidimensionalen Raum durch seinen Abstand vom Ursprung und zwei Winkel angegeben.
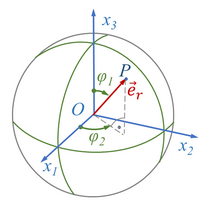
So ist der Vektor vom Ursprung zum Punkt P
mit
- .
Die Kugelkoordinaten kann man - ähnlich wie bei den Euler-Winkeln -zur Definition eines neuen, lokalen Koordinatensystems nutzen. Mit dem Flächen-Normalenvektor und den Tangentialvektoren zu φ1 und φ2 wird dabei eine neue Basis aufgespannt.
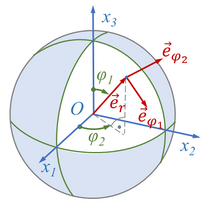
Die Koordinatentransformation erfolgt über
mit der Transformationsmatrix
Umrechnen von Euler-Winkel in Kugel-Koordinaten
Oft kann man räumliche Polarkoordinaten anschaulicher interpretieren als Euler-Winkel. Polarkoordinaten können allerdings zu Singularitäten führen wie in GYRQ. Wir schreiben hier deshalb eine Transformationsvorschrift an, mit der wir Euler-Winkel in Polarkoordinaten übersetzten können.
Dazu geben wir die räumlichen Koordinaten eines Punkts P mit einer Koordinatentransformation einerseits durch Euler-Drehmatrizen und andererseits durch Polarkoordinaten an. Dazu müssen wir auch die Drehung um eine dritte Achse verwenden. Wir wählen hier für die Euler-Transformation
mit den Winkeln φ1, φ2, φ3 sowie die Polarkoordinaten mit einer anschließenden Drehung um die -Achse
mit den Winkeln θ1, θ2, θ3.
Damit ein beliebiger Punkt nach beiden Transformationen gleich ist, muss
gelten. Diese Beziehungen kann man sukzessive nach den sin- und cos-Koeffizienten auflösen. Sie liefern
/* Euler-Winkel */
D[1](φ) := matrix([1,0,0],[0,cos(φ),sin(φ)],[0,-sin(φ),cos(φ)]);
D[2](φ) := matrix([cos(φ),0,-sin(φ)],[0,1,0],[sin(φ),0,cos(φ)]);
D[3](φ) := matrix([cos(φ),sin(φ),0],[-sin(φ),cos(φ),0],[0,0,1]);
/* Kugelkoordinanten */
D[12](θ,φ):= matrix([ cos(θ)*cos(φ), cos(θ)*sin(φ), -sin(θ)],
[ -sin(φ), cos(φ), 0 ],
[ sin(θ)*cos(φ), sin(θ)*sin(φ), cos(θ)]);
/* Zusammenhang Euler-Winkel - Kugelkoordinaten*/
/* Euler -> Kugel */
equ: matrix([a[x],a[y],a[z]]).D[3](θ[3]).D[12](θ[1],θ[2]) - matrix([a[x],a[y],a[z]]).D[3](φ[3]).D[1](φ[1]).D[2](φ[2]);
equ: flatten(makelist(coeff(args(equ),[a[x],a[y],a[z]][i]),i,1,3));
equ: makelist(equ[i]=0,i,1,9);
repl: solve([equ[5],equ[6],equ[7],equ[8],equ[9]],[cos(θ[3]),sin(θ[2]),cos(θ[2]),sin(θ[1]),cos(θ[1])])[1];
equ: transpose(subst(repl,equ));
repl: append(trigsimp(repl), subst([sin(φ[1])^2=1-cos(φ[1])^2],trigsimp(solve(equ[1],sin(θ[3])^2))));
equ: trigsimp(transpose(subst(repl,equ)));
Links
- Kugelkoordinaten auf Wikipedia
- Sources/Lexikon/Eulersche Winkel
- Quaternionen für Drehungen
- Geographische Koordinaten
Literature
- ...