Gelöste Aufgaben/FEAG: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (53 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
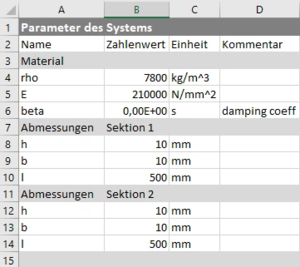
| Zeile 16: | Zeile 16: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:FEAG-01.png|mini|Lageplan| | [[Datei:FEAG-01.png|mini|Lageplan|left|200x200px]] | ||
Gesucht ist die Schwingung eines [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] | Gesucht ist die Schwingung eines [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]]s beim Loslassen aus der Ruhelage. Wir gehen nach dem Standardrezept der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]] vor, arbeiten also mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Arbeit]]. | ||
</onlyinclude> | </onlyinclude> | ||
= Lösung mit Matlab<sup>®</sup> = | |||
Interessant ist hier, dass - im Gegensatz zu Stablängsschwingungen - die Eigenfrequenz nicht ein gerades Vielfaches der untersten Eigenfrequenz ist. Falls Sie ein Saiteninstrument spielen, verstehen Sie sofort, warum das wichtig ist. | |||
[[Werkzeuge/Software/Maxima|Maxima]] können wir hier nicht gut gebrauchen: die Gleichungen werden zu umfangreich. Wir arbeiten also mehr mit numerischen Verfahren, da ist [[Werkzeuge/Software/Matlab|Matlab]] geeigneter. | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | |||
|text= | |||
Im Programm arbeiten wir mit einer dimensionslosen Formulierung - wir brauchen dafür eine Bezugszeit ''t<sub>Bez</sub>'' und eine Bezugslänge ''l<sub>Bez</sub>''. | |||
===Bezugsgrößen wählen=== | |||
Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe [[Gelöste Aufgaben/SKEB|SKEB]]): | |||
<table class="wikitable"> | |||
<tr><th> | |||
Analytische Lösung: homohener Lösungsanteil | |||
</th><th> | |||
Analytische Lösung: partikularer Lösungsanteil | |||
</th></tr> | |||
<tr><td style="width:50%; vertical-align:top"> | |||
Die homogene Bewegungsgleichung des [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balkens]] | |||
::<math>\varrho\,A\cdot\ddot{w}+E\,I\cdot{w}^{IV} = 0</math> | |||
hat Lösungen vom Typ | |||
::<math>\displaystyle w(x,t) = \sum_{i=1}^\infty W_i\cdot e^{\displaystyle \kappa_i\cdot x}\cdot e^{\displaystyle \omega_{0,i}\cdot t}</math> | |||
Wir bekommen zu jedem ''ω<sub>0</sub>'' vier ''κ'' | |||
::<math>\begin{array}{l} \displaystyle \kappa_1=+\frac{j\,\alpha}{\ell},\\ \displaystyle \kappa_2=-\frac{\alpha}{\ell},\\ \displaystyle \kappa_3=-\frac{j\,\alpha}{\ell},\\ \displaystyle \kappa_4=+\frac{\alpha}{\ell} \end{array} \;\;\text{ mit }\;\;\displaystyle\alpha^4 = \frac{{{\ell}^{4}}\,A\,\rho}{E\,I}\cdot {{\omega}_{0}^{2}}</math> | |||
Das ''α'' ist eine praktische Abkürzung, hinter der wir ''ω<sub>0</sub>'' verstecken. Anders als beim Dehnstab (SKER) finden wir hier keine analytische Beziehung, sondern nur die numerischen Beziehungen, für die unsere Randbedingungen erfüllt sind: | |||
::<math>\begin{array}{c}\alpha_1=1.875\ldots,\\ \alpha_2=4.694\ldots,\\ \alpha_3=7.854\ldots,\\ \vdots\end{array}</math> | |||
Die langsamste Eigenmode gehört zu ''α<sub>1</sub>'' mit der Periodendauer | |||
::<math>\displaystyle T^* = 0.5688\ldots \pi \ell^2 \sqrt{\frac{\varrho\,A}{E\,I}}</math>. | |||
Also wählen wir <math>t_{Bez} := T^*</math>. | |||
</td><td style="width:50%; vertical-align:top"> | |||
Die zugeordnete inhomogene Bewegungsgleichung des [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balkens]] | |||
::<math>E\,I\cdot{w}^{IV} = \varrho\,A\cdot g</math> | |||
hat die partikulare Lösung | |||
== | ::<math>\displaystyle E\,I\,{w}_p\left( x\right) =A\,g\,\varrho \,\ell^4 \cdot\left(\frac{{{\xi}^{4}}}{24}-\frac{{{\xi}^{3}}}{6}+\frac{{{\xi}^{2}}}{4}\right)</math> | ||
Die statische Auslenkung am unteren Ende ist | |||
demnach | |||
::<math>\displaystyle {{w}_{s}}=\frac{{{\ell}^{4}}\,A\,g\,\rho}{8\,E\,I}</math>. | |||
Wir wählen <math>\ell_{Bez} := w_s</math>. | |||
</td></tr> | |||
</table> | |||
=== '''System-Parameter des FEM-Modells''' === | |||
Für die Diskretisierung wählen wir als Anzahl der Finiten Elemente (Number Of Elements): | |||
::<math>\displaystyle I = 4 \;\;\;(\text{ im Matlab-Code: } NOE)</math> | |||
und damit je Element | |||
::<math>\displaystyle \ell_i = \frac{\ell_0}{I}</math>. | |||
Wir wählen die kubische Ansatzfunktionen aus dem Abschnitt [[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|Finite Elemente Methode]] je Element, also | |||
::<math>\begin{array}{crc} \phi_1 = & \left( \xi-1\right)^2 \cdot \left( 1+2\cdot \xi\right) \\ \phi_2 = & \left( \xi-1\right)^2 \cdot \xi \cdot \ell_{i} \\ \phi_3 = & \left( \xi^2 \cdot \left( 3-2 \cdot \xi\right) \right)\\ \phi_4 = & \left( \left( \xi-1\right) \cdot \xi^2 \cdot \ell_i \right)\end{array}</math> | |||
Für die numerisch Implementierung stört in dieser Darstellung das Element-spezifische ''ℓ<sub>i</sub>'' - die Elementlänge. Wir behelfen uns, indem wir die Ansatzfunktionen schreiben als | |||
::<math>\displaystyle \underbrace{ \left( \begin{array}{c} \phi_1\\ \phi_2\\ \phi_3\\ \phi_4 \end{array} \right)}_{\displaystyle =: \underline{\phi}} = \underbrace{ \left( \begin{array}{cccc} 1&0&0&0\\ 0&\ell_i&0&0\\ 0&0&1&0\\ 0&0&0&\ell_i\\ \end{array}\right)}_{\displaystyle =:\underline{\underline{d}}} \cdot \underbrace{ \left( \begin{array}{c} \left( \xi-1\right)^2 \cdot \left( 1+2\cdot \xi\right) \\ \left( \xi-1\right)^2 \cdot \xi \\ \left( \xi^2 \cdot \left( 3-2 \cdot \xi\right) \right)\\ \left( \left( \xi-1\right) \cdot \xi^2 \right)\end{array} \right)}_{\displaystyle =:\underline{\tilde{\phi}}}</math>, | |||
wobei wir die Ansatz-Polynome in <math>\underline{\tilde{\phi}}</math> verpacken. | |||
Das schaut unnötig komplex aus - allerdings stecken wir die Diagonal-Matrizen ''d'' (für jedes Element eine) in eine Matlab<sup>®</sup>-Variable, so dass sie dort nicht weiter auffällt. | |||
Die abhängigen Koordinaten des FEM-Modells sind dann zunächst - bis zum Einarbeiten der Randbedingungen - diese: | |||
::<math>\underline{Q}_t = \left(\begin{array}{c}W_0(t)\\\Phi_0(t)\\W_1(t)\\\vdots \\\Phi_I(t)\\W_I(t)\\ \end{array}\right)</math>. | |||
|code= | |||
<div><!-- CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC --></div> | |||
===Matlab=== | |||
====Classes==== | |||
In dieser CODE-Sektion kommt ein Beispiele zum Aufbau des Matlab<sup>®</sup>-Programms mit Klassen (Objektbasierte Programmierung) | |||
<ol> | |||
<li> | |||
<table> | |||
<tr><th>FEM-Section</th></tr> | |||
<tr class="mw-collapsible mw-collapsed"><td> | |||
<syntaxhighlight lang="Matlab" line='line' style="border:1px solid blue"> | |||
classdef FEM_Section | |||
% section section parameters | |||
properties | |||
rho; | |||
E; | |||
beta; | |||
h; | |||
b; | |||
l; | |||
end | |||
methods | |||
% Constructor | |||
function self = FEM_Section(parHashMap) | |||
self.rho = parHashMap('rho'); | |||
self.E = parHashMap('E'); | |||
self.beta = parHashMap('beta'); | |||
self.h = parHashMap('h'); | |||
self.b = parHashMap('b'); | |||
self.l = parHashMap('l'); | |||
end | |||
% end Constructor | |||
% start bending stiffness EI | |||
function EI = bendingStiffness(self) | |||
EI = self.E*1/12.*self.b*self.h^3; | |||
end | |||
% end bending stiffness | |||
% start cross-sectional area | |||
function A = cossecArea(self) | |||
A = self.b*self.h; | |||
end | |||
% end bending stiffness | |||
% start mass | |||
function m = mass(self) | |||
m = self.rho*self.b*self.h*self.l; | |||
end | |||
% end mass | |||
end | |||
end | |||
</syntaxhighlight></td></tr></table> | |||
</li><li> | |||
<table> | |||
<tr><th>FEM-Element-Model</th></tr> | |||
<tr class="mw-collapsible mw-collapsed"><td> | |||
<syntaxhighlight lang="Matlab" line='line' style="border:1px solid blue"> | |||
classdef FEM_Element_Modell | |||
% modell parameters | |||
properties | |||
type; % element type | |||
noe; % number of elements of this type | |||
noc; % number of coordinates per node | |||
phi; % trial-functions | |||
M; % element-mass matrix | |||
K; % element-stiffness matrix | |||
G; % element-load matrix (g) | |||
end | |||
methods | |||
% Constructor | |||
function self = FEM_Element_Modell(parHashMap) | |||
self.type = parHashMap('Type'); | |||
self.noe = parHashMap('NOE'); | |||
if self.type == 'EBB' | |||
% Euler-Bernoulli-Beam Elements | |||
self.phi = [[ 2,-3, 0, 1];... | |||
[ 1,-2, 1, 0];... | |||
[-2, 3, 0, 0];... | |||
[ 1,-1, 0, 0]]; | |||
self.noc = 2; | |||
elseif self.type == 'ER' | |||
% Extensible Rod type | |||
self.phi = [[-1, 1]; ... | |||
[ 1, 0]]; | |||
self.noc = 1; | |||
end | |||
[self.M,self.K,self.G] = self.ElementMassMatrix(); | |||
end | |||
% end Constructor | |||
function [M, K, G] = ElementMassMatrix(self) | |||
m = length(self.phi); | |||
M = zeros(m,m); | |||
K = zeros(m,m); | |||
G = zeros(m,1); | |||
for row = 1:m | |||
for col = 1:m | |||
M(row,col) = diff(... | |||
polyval(... | |||
polyint(... | |||
conv(self.phi(row,:),self.phi(col,:))),... | |||
[0,1])); | |||
if self.type == 'EBB' % -> second derivs | |||
K(row,col) = diff(... | |||
polyval(... | |||
polyint(... | |||
conv(polyder(polyder(self.phi(row,:))),polyder(polyder(self.phi(col,:))))),... | |||
[0,1])); | |||
elseif self.type == 'ER' % -> first derivs | |||
K(row,col) = diff(... | |||
polyval(... | |||
polyint(... | |||
conv(polyder(self.phi(row,:)),polyder(self.phi(col,:)))),... | |||
[0,1])); | |||
end | |||
end | |||
G(row,1) = diff(... | |||
polyval(... | |||
polyint(... | |||
self.phi(row,:)),... | |||
[0,1])); | |||
end | |||
end | |||
end | |||
end | |||
</syntaxhighlight></td></tr></table> | |||
</li><li> | |||
<table> | |||
<tr><th>FEM-Container</th></tr> | |||
<tr class="mw-collapsible mw-collapsed"><td> | |||
<syntaxhighlight lang="Matlab" line='line' style="border:1px solid blue"> | |||
classdef FEM_Container | |||
% holds all system matrics | |||
properties | |||
% matrices | |||
M; % mass matrix | |||
D; % damping matrix | |||
K; % stiffness matrix | |||
G; % gravitational Loading | |||
d; % scalting matrix with l[i]-Element | |||
% rod length | |||
l; % length | |||
% model properties | |||
NOE; % number of elements | |||
NON; % number of nodes | |||
NOC % number of coordinates per node | |||
NOQ % number of coordinates in total | |||
g; % 9.81 m/s^2 | |||
% boundary conditions | |||
free; | |||
disabled; | |||
% functions | |||
trials; | |||
% solution | |||
samples; % number of samples when plotting with points | |||
end | |||
methods | |||
% Constructor | |||
function self = FEM_Container(bezug,system,boundaries,element) | |||
% declarations | |||
NOE = sum(element.noe); % number of all elements in all sections | |||
NON = NOE+1; % number of nodes | |||
NOC = element.noc; % number of coordinates per node | |||
NOQ = NON*NOC; % number of coordintes | |||
self.NOE = NOE; | |||
self.NON = NON; | |||
self.NOC = NOC; | |||
self.NOQ = NOQ; | |||
% number of samples when plotting | |||
self. samples = 21; | |||
% global params | |||
self.g = 9.81/(bezug('l_ref')/bezug('t_ref')^2); | |||
% FE-lengths | |||
self.l = [0]; | |||
for sec = 1: length(system) | |||
for ele = 1: element.noe(sec) | |||
self.l = [self.l, self.l(length(self.l))+system(sec).l/element.noe(sec)]; | |||
end | |||
end | |||
% initialize system matrices | |||
[self.M, self.K, self.G, self.d] = self.systemMatrices(system, element); | |||
% collect boundary conditions | |||
free = linspace(1,1, element.noc*(sum(element.noe)+1)); | |||
touch = [1]; | |||
for sec = 1: length(element.noe) | |||
touch = [touch,touch(length(touch))+element.noc*element.noe(sec)]; | |||
end | |||
for i= 1:min(length(touch),length(boundaries)) | |||
nodeNo= touch(i); | |||
free(nodeNo:nodeNo+element.noc-1) = boundaries(i).free; | |||
end | |||
disabled = ~free; | |||
self.free = (1:length(free)).*free; | |||
self.free(self.free==0)=[]; | |||
disabled = (1:length(disabled)).*disabled; | |||
self.disabled = (1:length(disabled)).*disabled; | |||
self.disabled(self.disabled==0)=[]; | |||
% trial functions | |||
self.trials = element.phi; | |||
end | |||
% end Constructor | |||
% start system matrices | |||
function [M,K,G,d] = systemMatrices(self, system, element) | |||
M = zeros(self.NOQ,self.NOQ); | |||
K = zeros(self.NOQ,self.NOQ); | |||
G = zeros(self.NOQ, 1 ); | |||
d = zeros(4, 4, self.NOE ); | |||
g = self.g; | |||
e = 0;% counter for all elements of all sections | |||
for section = 1: length(element.noe) | |||
L = system(section).l/element.noe(section); | |||
m = system(section).rho*system(section).cossecArea()*L; | |||
% beinding stiffness | |||
b = system(section).bendingStiffness()/L^3; | |||
for i = 1:element.noe(section) | |||
e = e+1; | |||
if element.type=='EBB' | |||
d(:,:,e) = diag([1,L,1,L]); % diagnoal matrix with l[i]-factors | |||
elseif element.type=='ER' | |||
d(:,:,e) = diag([1,1]); | |||
end | |||
% | |||
j = 2*(e-1)+1; | |||
M(j:j+3,j:j+3) = M(j:j+3,j:j+3)+m* d(:,:,e)*element.M*d(:,:,e); | |||
K(j:j+3,j:j+3) = K(j:j+3,j:j+3)+b* d(:,:,e)*element.K*d(:,:,e); | |||
G(j:j+3,1) = G(j:j+3,1) +m*g*d(:,:,e)*element.G; | |||
end | |||
end | |||
end | |||
% end system matrices | |||
% start boudaryconditions | |||
function [M,K,G] = constrained(self) | |||
M = self.M(self.free,self.free); | |||
K = self.K(self.free,self.free); | |||
G = self.G(self.free, 1 ); | |||
end | |||
% end system matrices | |||
% start eigensystem | |||
function [V,D] = eigensystem(self) | |||
% ODE: A q + B q = 0 | |||
% = - = - - | |||
% define system matrices | |||
[A,B,G] = self.constrained(); | |||
%S = linsolve(A,-B); | |||
S = inv(A)*(-B); | |||
% eigensystem | |||
[V,D] = eig(S); | |||
end | |||
% end eigensystem | |||
% start particular solution | |||
function Q = particularSolution(self) | |||
% ODE: A q + B q = G | |||
% = - = - - | |||
% define system matrices | |||
[A,B,G] = self.constrained(); | |||
Q = linsolve(B,G); | |||
end | |||
% end particular solution | |||
end | |||
end | |||
</syntaxhighlight></td></tr></table> | |||
</li> | |||
</ol> | |||
====Eingabe-Parameter aus Excel==== | |||
< | <table> | ||
<tr> | |||
<td>[[Datei:FEAG-EXCEL-Eingabe-1.png|mini|0) Bezugsgrößen.]]</td><tr/><tr> | |||
<td>[[Datei:FEAG-EXCEL-Eingabe-4.png|mini|2) Modell]]</td><tr/><tr> | |||
<td>[[Datei:FEAG-EXCEL-Eingabe-2.png|mini|1) System]]</td><tr/><tr> | |||
<td>[[Datei:FEAG-EXCEL-Eingabe-3.png|mini|2) Randbedingungen]]</td> | |||
</tr> | |||
</table> | |||
}} | }} | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
Die Gleichgewichtsbedingung mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] setzen sich additiv aus | |||
::<math>\displaystyle \delta W = \sum_{i=1}^I \left(\delta W^a_i - \delta \Pi_i \right) + \delta W^a_R</math>, | |||
zusammen - also den virtuellen Arbeiten je Element zuzüglich von virtuellen Arbeiten am Rand. In unserem Beispiel haben wir allerdings keine eingeprägten, äußeren Lasten am Rand, also ist | |||
::<math>\delta W^a_R = 0</math>. | |||
Je Element erfassen wir die virtuellen Arbeiten durch Element-Matrizen. So ist z.B. für die virtuelle Formänderungsenergie (vgl. [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]) | |||
::<math>\delta \Pi_i = \left(\delta W_{i-1}, \delta \Phi_{i-1}, \delta W_{i} , \delta \Phi_{i}\right) \cdot \underline{\underline{K}}_i\cdot \left(\begin{array}{c}W_{i-1}(t)\\\Phi_{i-1}(t)\\W_{i}(t)\\\Phi_{i}(t) \end{array}\right)</math> | |||
mit der Element-Steifigkeitsmatrix <math>\underline{\underline{K}}_i</math>. | |||
Aus der [[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]] könnten wir die Element-Matrizen der virtuellen Arbeit der [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'schen Trägheitskraft]] sowie der [[Sources/Lexikon/Virtuelle Formänderungsenergie|Virtuelle Formänderungsenergie]] herauskopieren. Auch die "rechte Seite" mit der virtuelle Arbeit der Gewichtskraft aus | |||
::<math>\displaystyle \delta W^{a,g}_i = \int_{\ell_i} \varrho\; A \; g \cdot \delta w(x) \;dx_i</math>, | |||
könnten wir als Element-Lastmatrix (Spaltenmatrix) abspeichern. | |||
::<math>\displaystyle \underline{G}_i = \frac{\varrho\,A\, g\, \ell_i}{2} \cdot \left(\begin{array}{c}+1\\\displaystyle +\frac{\ell_i}{6}\\+1\\\displaystyle -\frac{\ell_i}{6}\end{array}\right)</math>. | |||
Dass es auch anders geht,sehen Sie in der Definition der Matlab<sup>®</sup>-Klasse FEM_Element_Modell, bei der die Element direkt aus den Trial-Functions - hier den <math>\underline{\tilde{\phi}}</math> - | |||
hergeleitet. werden: | |||
<pre> | |||
: | |||
K(row,col) = diff(... | |||
polyval(... | |||
polyint(... | |||
conv(polyder(self.phi(row,:)),polyder(self.phi(col,:)))),... | |||
[0,1])); | |||
: | |||
</pre> | |||
=== Komponieren der System-Matrizen === | |||
Die System-Matrizen des Gesamt–Systems komponieren wir nun durch Hinzuaddieren der Anteile je Element. | |||
Beispiel: die Gesamt-Steifigkeitsmatrix für I=2: | |||
::<math>\displaystyle \underline{\underline{K}} = \frac{E\,I}{\ell_i^3} \cdot \left( \begin{array}{ccccc} | |||
{\color{red}{+12}}&{\color{red}{+6}}&{\color{red}{-12}}&{\color{red}{+6}}&0&0\\ | |||
{\color{red}{+6\ell_i}}&{\color{red}{+4\ell_i^2}}&{\color{red}{-6\ell_i}}&{\color{red}{+2\ell_i^2}}&0&0\\ | |||
{\color{red}{-12}}&{\color{red}{-6}}&{\color{red}{+12}} {\color{green}{+12}}&{\color{red}{-6}} {\color{green}{+6}}&{\color{green}{-12}}&{\color{green}{+6}}\\ | |||
{\color{red}{+6\ell_i}}&{\color{red}{2\ell_i^2}}&{\color{red}{-6\ell_i}} {\color{green}{+6\ell_i}}&{\color{red}{+2\ell_i^2}} {\color{green}{+2\ell_i^2}}&{\color{green}{-6\ell_i}}&{\color{green}{+2\ell_i^2}}\\ | |||
0&0&{\color{green}{-12}}&{\color{green}{-6}}&{\color{green}{+12}}&{\color{green}{-6}}\\ | |||
0&0&{\color{green}{+6\ell_i}}&{\color{green}{2\ell_i^2}}&{\color{green}{-6\ell_i}}&{\color{green}{+2\ell_i^2}} | |||
\end{array} \right)</math> | |||
Die Beiträge der zwei Elemente sind hier in rot bzw. grün eingefärbt. | |||
Dieses "Hinzuaddieren" passiert in [[Gelöste Aufgaben/FEAG/FEAG-Matlab|Matlab]] hier: | |||
<pre> | |||
: | |||
e = 0;% counter for all elements of all sections | |||
for section = 1: length(element.noe) | |||
: | |||
for i = 1:element.noe(section) | |||
e = e+1; | |||
: | |||
j = 2*(e-1)+1; | |||
: | |||
K(j:j+3,j:j+3) = K(j:j+3,j:j+3)+b* d(:,:,e)*element.K*d(:,:,e); | |||
: | |||
end | |||
: | |||
</pre> | |||
In Matrix-Schreibweise lautet die Bewegungsgleichung des Gesamt-Systems jetzt: | |||
::<math>\underline{\underline{M}}\cdot\underline{\ddot{Q}} + \underline{\underline{K}}\cdot\underline{Q} = \underline{G}</math>. | |||
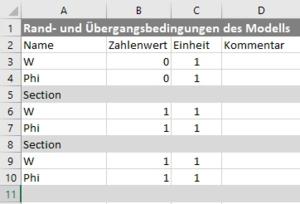
=== Einarbeiten der Randbedingungen === | |||
[[Datei:FEAG-11-Randbedingungeneinarbeiten.png|mini|Randbedingungen einarbeiten.]] | |||
Die Randbedingungen arbeiten wir ein, indem wir zeilenweise (für ''δW'' und ''δΦ'') und spaltenweise (für ''W'' und ''Φ'') streichen. | |||
Hier sind es | |||
* die erste Zeile/Spalte für <span style="color:#000080">''W<sub>0</sub>'' (blau)</span> und | |||
* die zweite Zeile / Spalte für <span style="color:#008000">''Φ<sub>0</sub>'' (grün)</span>. | |||
|code=NONE - see below}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | |||
|text= | |||
Die Lösung des Anfangs- und Randwertproblems ist in diesem Lösungsansatz mit Matlab<sup>®</sup> um die Klasse "FEM_Container" herum aufgebaut - in ihr sind alle Parameter und Lösungsprozesse beschrieben. | |||
Hier heißt die Instanz des Modells | |||
* mathModel | |||
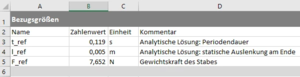
In diesem Container sind alle Parameter und Zustandsgrößen des Modells bereits dimensionslos gemacht - und zwar mit den oben genannten Bezugsgrößen, die in der Excel-Eingabedatei im Blatt "0) Bezugsgrößen" definiert sind. | |||
Die Lösung des Anfangswertproblems setzt sich aus zwei Teilen zusammen: | |||
* der partikularen Lösung, die die Rechte Seite "''G''" erfüllt und | |||
* der homogenen Lösung, die die Rechte Seite "''0''" erfüllt. | |||
Die Gesamtlösung ''Q<sub>t</sub>'' setzt sich nun - bei diesem linearen System - additiv aus partikularer ''Q<sub>p</sub>'' und ''Q<sub>h</sub>'' homogener Lösung zusammen: | |||
::<math>\underline{Q}_t(t) = \underline{Q}_p(t) + \underline{Q}_h(t)</math> | |||
=== Particular Solution === | |||
[[Datei:FEAG-12-particulareLösung.png|mini|Particulare Lösung.]] | [[Datei:FEAG-12-particulareLösung.png|mini|Particulare Lösung.]] | ||
[[ | Die rechte Seite der Bewegungsgleichung ''G'' ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung ''Q<sub>p</sub>'' statisch, wir suchen nach der Lösung des Gleichungssystems | ||
:: <math>\underline{\underline{K}}\cdot\underline{Q}_p = \underline{G}</math> | |||
und die ist - mit der Normierung durch ''w<sub>s</sub>'' - | |||
<pre> | |||
>> Qp | |||
Qp = | |||
0 | |||
0 | |||
0.1055 | |||
0.0042 | |||
0.3542 | |||
0.0064 | |||
0.6680 | |||
0.0072 | |||
1.0000 | |||
0.0073 | |||
</pre> | |||
Diese Lösung tragen wir - elementweise - auf. | |||
=== Homogene Lösung === | |||
Zur Lösung der homogenen Bewegungsgleichung | |||
::<math>\underline{\underline{M}}\cdot\underline{\ddot{Q}} + \underline{\underline{K}}\cdot\underline{Q} = \underline{0}</math> | |||
setzen wir an | |||
::<math>\displaystyle \underline{Q}_h = \underline{\hat{Q}}_h\cdot e^{\lambda\cdot t}</math> | |||
und erhalten das [[Werkzeuge/Lösungsbausteine der Mathematik/Eigenwertprobleme|Eigenwertproblem]] | |||
::<math>\underbrace{\left(\lambda^2 \underline{\underline{M}} + \underline{\underline{K}}\right)}_{=: \displaystyle \underline{\underline{D}}}\cdot\underline{\hat{Q}}_h = \underline{0}</math> | |||
mit | |||
<table> | |||
<tr><td>den Eigenwerten</td><td><math>\lambda</math> und</td></tr> | |||
<tr><td>den Egenvektoren</td><td><math>\displaystyle \underline{\hat{Q}}_{h}</math>.</td></tr> | |||
</table> | |||
Für die Berechnung der Eigenwerte λ müssen wir die Abkürzung | |||
::<math>\lambda^2 = \Lambda</math> | |||
einführen. Damit arbeitet die Matlab<sup>®</sup>-Routine "eig()", die in "mathModel.eigensystem()" implementiert ist. | |||
Acht Eigenwerte kommen aus der Bedingung <math>\det(\underline{\underline{D}})=0</math>, diese <math>\Lambda_i</math> werden auf der Spur der Matrix D abgelegt: | |||
<pre> | |||
>> D | |||
D = | |||
1.0e+06 * | |||
-2.9006 0 0 0 0 0 0 0 | |||
0 -1.0774 0 0 0 0 0 0 | |||
0 0 -0.4287 0 0 0 0 0 | |||
0 0 0 -0.1662 0 0 0 0 | |||
0 0 0 0 -0.0480 0 0 0 | |||
0 0 0 0 0 -0.0123 0 0 | |||
0 0 0 0 0 0 -0.0016 0 | |||
0 0 0 0 0 0 0 -0.0000 | |||
</pre> | |||
Die zugehörigen dimensionslosen Periodendauern sind | |||
::<math>\begin{array}{ll}T_1 = & 0.0037\\ T_2 = & 0.0061\\ T_3 = & 0.0096\\ T_4 = & 0.0154 \\ T_5 = & 0.0287 \\ T_6 = & 0.0566 \\ T_7 = & 0.1594 \\ T_8 = & 1.0000\end{array}</math>. | |||
Und offensichtlich fällt die längste Periodendauer ''T<sub>8</sub>'' mit der analytisch berechneten untersten Schwingunsperiode ''T<sup>*</sup>'' zusammen. | |||
Die zugehörigen Eigenvektoren stehen in ''V'': | |||
<pre> | |||
>> V | |||
V = | |||
-0.0579 0.2951 -0.0687 0.3043 0.4561 0.5309 -0.3197 -0.0780 | |||
-0.0129 0.0882 -0.0805 -0.0578 -0.0115 0.0064 -0.0096 -0.0032 | |||
-0.0884 -0.1020 0.4873 -0.0417 -0.4707 0.0160 -0.5469 -0.2721 | |||
-0.0364 0.1230 0.0134 0.0659 -0.0007 -0.0222 0.0019 -0.0051 | |||
-0.1652 -0.4100 -0.2420 -0.1979 0.4058 -0.4268 -0.1035 -0.5270 | |||
-0.0763 0.0330 0.0704 -0.0601 0.0098 0.0106 0.0163 -0.0059 | |||
-0.9540 -0.8313 -0.8232 0.9212 -0.6357 0.7308 0.7663 -0.8013 | |||
-0.2099 -0.1390 -0.0999 0.0809 -0.0389 0.0315 0.0200 -0.0060 | |||
</pre> | |||
Die Eigenvektoren in ''V'' spannen nun den Nullraum (nullspace) der Matrix auf, es ist | |||
::<math>\underline{\underline{V}} = \left( \;\underline{\hat{Q}}_{h,1}\;,\;\underline{\hat{Q}}_{h,2}\;,\;\underline{\hat{Q}}_{h,3}\;,\;\underline{\hat{Q}}_{h,4}\;,\;\underline{\hat{Q}}_{h,5}\;,\;\underline{\hat{Q}}_{h,6}\;,\;\underline{\hat{Q}}_{h,7}\;,\;\underline{\hat{Q}}_{h,8}\;\right)</math> | |||
Die homogene Lösung der Bewegungsgleichung lautet damit | |||
::<math>\displaystyle \underline{{Q}}_{h}(t) = \sum_{i=1}^8 C_i \cdot \underline{\hat{Q}}_{h,i} \cdot e^{\displaystyle j\cdot \omega_{0,i} \cdot \tau} </math> | |||
mit den acht Integrationskonstanten ''C<sub>i</sub>'' . Durch die komplexen Eigenwerte sind die Integrationskonstanten nun (eigentlich) auch komplexwertig. Darum kommen in diesem Fall herum, weil die Anfangsgeschwindigkeit des Balkens beim Loslassen Null ist - wir also nur cos-Anteile berücksichtigen müssen. Und die gehören wiederum zum Realteil der Exponential-Funktion. | |||
Die ''C<sub>i</sub>'' sind nun die Konstanten, die wir brauchen, um die Lösung an Anfangsbedingungen anzupassen. | |||
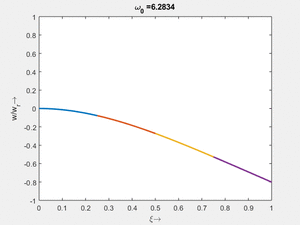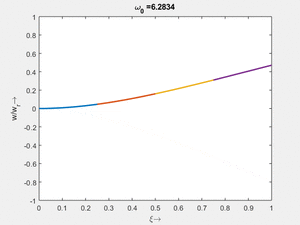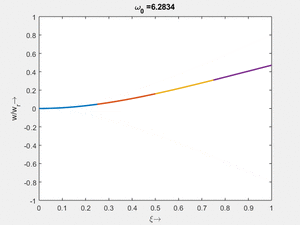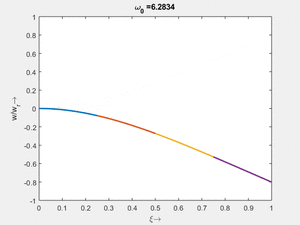
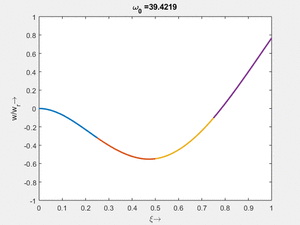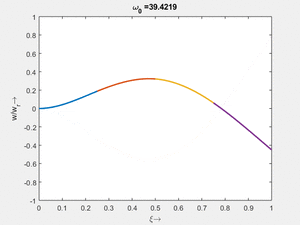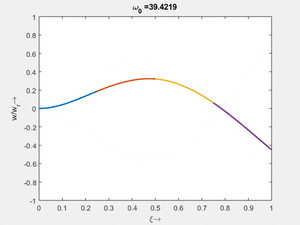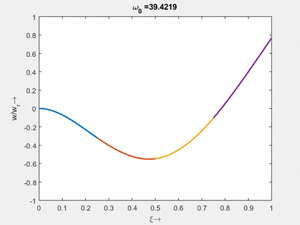
Vorher schauen wir uns die Lösung jeweils zu einer Eigenfrequenz ''ω<sub>i</sub>'' an. Diese Funktionen heißen Modalformen ''ϕ(x)'' und deren Schwingungen können wir plotten: | |||
<table> | <table> | ||
<tr><th>Mode</th><th>Modalform ''ϕ<sub>j</sub>(x)''</th><th>Mode</th><th>Modalform ''ϕ<sub>j</sub>(x)''</th></tr> | |||
<tr> | <tr> | ||
<td>[[Datei: | <td>#8<br/><math>\displaystyle \omega_{0,8} = 1.000\cdot \frac{2 \pi}{T_{ref}}</math></td> | ||
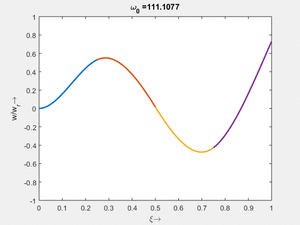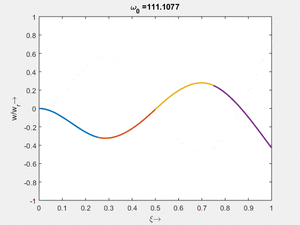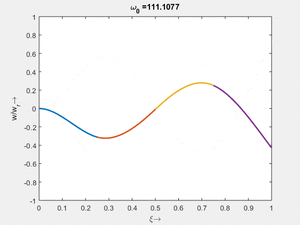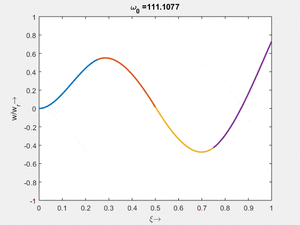
<td>[[Datei: | <td>[[Datei:Feag-mode-001.gif|mini|Mode #1]]</td> | ||
<td>[[Datei: | <td>#7<br/><math>\displaystyle \omega_{0,7} = 6.2742\cdot \frac{2 \pi}{T_{ref}}</math></td> | ||
<td>[[Datei:Feag-mode-002.gif|mini|Mode #2]]</td> | |||
</tr> | |||
<tr> | |||
<td>#6<br/><math>\displaystyle \omega_{0,6} = 17.6833\cdot \frac{2 \pi}{T_{ref}}</math></td> | |||
<td>[[Datei:Feag-mode-003.gif|mini|Mode #3]] | |||
</td> | |||
<td>#5<br/><math>\displaystyle \omega_{0,5} = 34.8854\cdot \frac{2 \pi}{T_{ref}}</math></td> | |||
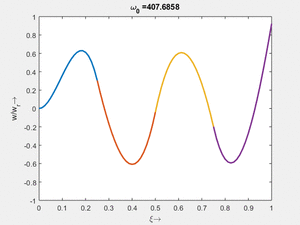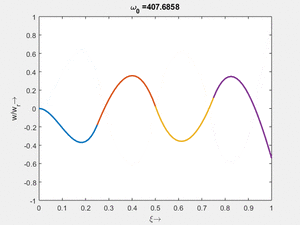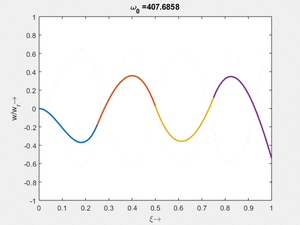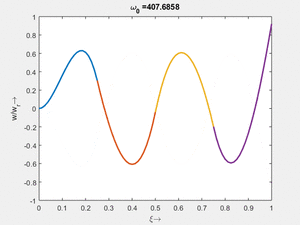
<td>[[Datei:Feag-mode-004.gif|mini|Mode #4]]</td> | |||
</tr> | |||
<tr> | |||
<td>#4<br/><math>\displaystyle \omega_{0,4} = 64.8852\cdot \frac{2 \pi}{T_{ref}}</math></td> | |||
<td>[[Datei:Feag-mode-005.gif|mini|Mode #5]] | |||
</td> | |||
<td>#3<br/><math>\displaystyle \omega_{0,3} = 104.2059\cdot \frac{2 \pi}{T_{ref}}</math></td> | |||
<td>[[Datei:Feag-mode-006.gif|mini|Mode #6]] | |||
</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
[[Datei:FEAG- | [[Datei:FEAG-modes-all.png|mini|Modalformen]]Alle acht Moden ''ϕ<sub>j</sub>'' können wir auch zum Zeitpunkt ''τ=0'' übereinander darstellen: | ||
{{MyTip|title=Zur Euler-Bernoulli-Hypothese|text= | |||
Praktisch haben die höheren Moden kaum Relevanz - meist klingen sie durch Dämpfung schnell ab. Man sieht allerdings bereits an der Schwingungs-Form, dass hier die Länge zwischen zwei Knoten nicht mehr sehr klein ist im Vergleich zur Höhe. Und das führt dazu, dass Schubverformungen eine Rolle spielen. Wir müssen zum [[Timoshenko-Balken]] wechseln ....}} | |||
|code= | |||
<div><!-- --></div> | |||
===Matlab<sup>®</sup>=== | |||
====Main Script==== | |||
<table> | |||
<tr><th>Main - part I (preprocessor)</th></tr> | |||
<tr class="mw-collapsible mw-collapsed"><td> | |||
<syntaxhighlight lang="Matlab" line='line' style="border:1px solid blue"> | |||
% DESCRIPTION | |||
% _____________________________________ | |||
% computes solutions for straight rods | |||
% reads parameters from | |||
% FEAG.xlsx | |||
% writes results to | |||
% feag-*.gif | |||
% feag-*.png | |||
% process | |||
% uses own functions | |||
% - readSystemParameters(fileName); | |||
% - getUnitConversion | |||
% - | |||
% uses classes | |||
% - FEM_Container | |||
% - FEM_Element_Modell | |||
% - FEM_Section | |||
% - FEM_BoundaryCondition | |||
% uses MATLAB functions | |||
% - linsolve | |||
% - eig | |||
cd('C:\Users\abs384\OneDrive\Confluence Sources\FEAG'); | |||
addpath(['../Matlab/Functions']); | |||
addpath(['../Matlab/Classes']); | |||
%%**************************************** | |||
% PREPROCESSOR * | |||
% **************************************** | |||
fileName = 'FEAG'; | |||
[ bezug, system, boundaries, element, err ] = readSystemParameters(fileName); | |||
%% | |||
mathModel = FEM_Container(bezug,system,boundaries,element); | |||
%% | |||
: | |||
: | |||
: | |||
</syntaxhighlight></td></tr></table> | |||
<table> | |||
<tr><th>Main - part II (partikulare Lösung)</th></tr> | |||
<tr class="mw-collapsible mw-collapsed"><td> | |||
<syntaxhighlight lang="Matlab" line='line' style="border:1px solid blue"> | |||
: | |||
: | |||
: | |||
%% ***************************************************************************/ | |||
% p a r t i c u l a r s o l u t i o n */ | |||
% ***************************************************************************/ | |||
NOV = length(mathModel.free)+length(mathModel.disabled); | |||
% initiate particular solution Qp | |||
Qp = zeros(NOV,1); | |||
Q = mathModel.particularSolution(); | |||
Qp(mathModel.free,:)=Q; | |||
% get coordinates of nodes | |||
L = mathModel.l(length(mathModel.l)); | |||
% plot particular solution | |||
for ele= 1: mathModel.NOE | |||
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples); | |||
plot(xi,Qp(2*ele-1:2*ele+2,1)'*(mathModel.d(:,:,ele)*phi), 'LineWidth',4); hold on; | |||
end | |||
plot(mathModel.l/mathModel.l(length(mathModel.l)),Qp(1:2:length(Qp)),'ro', 'LineWidth',2); | |||
xlabel('\xi\rightarrow'); | |||
ylabel('w/w_s\rightarrow'); | |||
hold off; | |||
</syntaxhighlight></td></tr></table> | |||
<table> | |||
<tr><th>Main - part III (homogene Lösung)</th></tr> | |||
<tr class="mw-collapsible mw-collapsed"><td> | |||
<syntaxhighlight lang="Matlab" line='line' style="border:1px solid blue"> | |||
: | |||
: | |||
: | |||
%% ***************************************************************************/ | |||
% * h o m o g e n e o u s s o l u t i o n */ | |||
% ***************************************************************************/ | |||
[V,D] =mathModel.eigensystem(); | |||
% eigenfrequencies of system | |||
omega = sqrt(diag(-D)); | |||
Qh = zeros(NOV,length(mathModel.free)); | |||
Qh(mathModel.free,:) = V(:,:); | |||
% plot modes | |||
for mode =length(mathModel.free):-1:1 | |||
for ele= 1: mathModel.NOE | |||
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples); | |||
plot(xi,Qh(2*ele-1:2*ele+2,mode)'*(mathModel.d(:,:,ele)*phi), 'LineWidth',2); hold on; | |||
end | |||
plot(mathModel.l/mathModel.l(length(mathModel.l)),Qh(1:2:length(Qp),mode),'ro', 'LineWidth',2); | |||
xlabel('\xi\rightarrow'); | |||
ylabel('w/w_r\rightarrow'); | |||
end | |||
hold off; | |||
</syntaxhighlight></td></tr></table> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Adapt to Initial Conditions | |||
|text= | |||
Die acht reell-wertigen Integrationskonstanten ''C<sub>i</sub>'' bestimmen wir aus den Anfangsbedingungen für den Balken, nämlich | |||
::<math>\underline{Q}_t(0) = \underline{0} \text{ und } \underline{\dot{Q}}_t(0) = \underline{0} </math> , | |||
also | |||
::<math>\begin{array}{llcll} W_1(0) &= 0&\;\;\;&\dot{W}_1(0) & = 0\\ \Phi_1(0) &= 0& &\dot{\Phi}_1(0)& = 0\\ W_2(0) &= 0& &\dot{W}_2(0) & = 0\\ \Phi_2(0) &= 0& &\dot{\Phi}_2(0)& = 0\\ W_3(0) &= 0& &\dot{W}_4(0) & = 0\\ \Phi_3(0) &= 0& &\dot{\Phi}_3(0)& = 0\\ W_4(0) &= 0& &\dot{W}_4(0) & = 0\\ \Phi_4(0) &= 0& &\dot{\Phi}_4(0)& = 0\\ \end{array}</math>. | |||
Wenn wir die ''C''<sub>i</sub> komplexwertig denken, so stehen hier 16 Anfangsbedingungen für acht komplexe ''C''<sub>i</sub> . | |||
Denken wir die ''C''<sub>i</sub> gleich reelwertig, so können wir die acht Anfangsbedingungen in der rechten Spalte weglassen - sie sind dann implizit mit erfüllt - für unser spezielles Anfangswertproblem. | |||
Die Anfangsbedingung für die Gesamtlösung lautet nun: | |||
::<math>\underline{Q}_p + \underline{Q}_h|_{\tau=0} = \underline{0}</math> , | |||
also | |||
::<math>\underline{\underline{V}}\cdot \underbrace{\left(\begin{array}{c}C_1\\C_2\\C_3\\C_4\\C_5\\C_6\\C_7\\C_8\end{array}\right)}_{\displaystyle =:\underline{C}} = -\underline{Q}_p</math> | |||
Wir finden | |||
::<math>\underline{C} = \left(\begin{array}{l}+6.87897955904839E^{-07}\\-4.64941679695326E^{-06}\\+1.66295172107590E^{-05}\\+4.37871009978632E^{-05}\\+0.000288375976158946\\+0.00145539720136673\\-0.0186576428599944\\-1.26472054045511\end{array}\right)</math> . | |||
und damit | |||
::<math>\displaystyle \underline{Q}_{t}(t) = \underline{Q}_{p} + \sum_{i=1}^8 C_i\cdot \underline{\hat{Q}}_{h,i} \cos{\omega_{0,i}\cdot\tau} </math> . | |||
Offensichtlich ist der Beitrag der Mode 8 (also der langsamsten Mode) bei weitem am größten Anteil an ''Q<sub>h</sub>''. Das können wir auch in der Animation der Lösung - also das Loslassen des Balken aus der Ruhe heraus - sehen. | |||
|code= | |||
<div><!-- CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC --></div> | |||
===Matlab<sup>®</sup>=== | |||
====Main Script==== | |||
<table> | |||
<tr><th>Main - part IV (adapt to initial conditions)</th></tr> | |||
<tr class="mw-collapsible mw-collapsed"><td> | |||
<syntaxhighlight lang="Matlab" line='line' style="border:1px solid blue"> | |||
: | |||
: | |||
: | |||
%% ***************************************************************************/ | |||
% t o t a l ( c o m p o s e d ) s o l u t i o n */ | |||
% ***************************************************************************/ | |||
C = linsolve(Qh(mathModel.free,:),Qp(mathModel.free,1)); | |||
Qi = zeros(NOV,length(mathModel.free)); | |||
Qi(mathModel.free,:) = Qh(mathModel.free,:)*diag(C); | |||
for ele= 1: mathModel.NOE | |||
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples); | |||
plot(xi,Qp(2*ele-1:2*ele+2,1)'*(mathModel.d(:,:,ele)*phi), 'Color', [0.8 0.8 0.8], 'LineWidth',8); hold on; | |||
end | |||
for mode =1 : length(mathModel.free) | |||
for ele= 1: mathModel.NOE | |||
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples); | |||
plot(xi,Qi(2*ele-1:2*ele+2,mode)'*(mathModel.d(:,:,ele)*phi), 'LineWidth',2); hold on; | |||
end | |||
end | |||
hold off; | |||
</syntaxhighlight></td></tr></table>}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
Die FEM-Lösung im Zeitbereich, angepasst an die Anfangsbedingungen, sieht nun so aus: | |||
<table> | <table> | ||
<tr><td> | <tr><td style="width:50%; vertical-align:top"> | ||
[[Datei:FEAG-SchwingungImZeitbereich.png|mini|Lösung im Zeitbereich - hier für ''I=4''.]] | |||
</td><td style="width:50%; vertical-align:top"> | |||
[[Datei:FEAG-timeDomainAnimation.gif|mini|Animation in Time Domain - hier für ''I=4''.]] | |||
</td></tr> | |||
</table> | </table> | ||
|code= | |||
<div><!-- CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC --></div> | |||
===Matlab<sup>®</sup>=== | |||
====Main Script==== | |||
<table> | |||
<tr><th>Main - part IV (adapt to initial conditions)</th></tr> | |||
<tr class="mw-collapsible mw-collapsed"><td> | |||
<syntaxhighlight lang="Matlab" line='line' style="border:1px solid blue"> | |||
: | |||
: | |||
: | |||
%% animated shape .... | |||
tau = linspace(0,3,3*21); | |||
h = figure; | |||
axis tight manual % this ensures that getframe() returns a consistent size | |||
fileName = strcat('feag-initial-value-solution-animation.gif'); | |||
for step = tau | |||
hold off; | |||
for ele= 1: mathModel.NOE | |||
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples); | |||
disp = Qp(2*ele-1:2*ele+2,1)'*(mathModel.d(:,:,ele)*phi); | |||
for mode =length(mathModel.free):-1:1 | |||
disp = disp - Qi(2*ele-1:2*ele+2,mode)'*(mathModel.d(:,:,ele)*phi)*cos(2*pi*omega(mode)/omega(length(omega))*step); | |||
end | |||
plot(xi,disp, 'LineWidth',2); hold on; | |||
axis([0 1 -0.1 2.1]); | |||
set(gca,'Ydir','reverse') | |||
xlabel('\xi\rightarrow'); | |||
ylabel('w/w_r\rightarrow'); | |||
end | |||
title('initial value solution'); | |||
drawnow | |||
% Capture the plot as an image | |||
frame = getframe(h); | |||
im = frame2im(frame); | |||
[imind,cm] = rgb2ind(im,256); | |||
% Write to the GIF File | |||
if step == 0 | |||
imwrite(imind,cm,fileName,'gif', 'Loopcount',inf,'DelayTime',0); | |||
else | |||
imwrite(imind,cm,fileName,'gif','WriteMode','append','DelayTime',0); | |||
end | |||
end | |||
hold off; | |||
%% time domain .... | |||
tau = linspace(0,3,3*71); | |||
fileName = 'feag-initial-value-solution-W.gif'; | |||
pick = 3:2:mathModel.NOQ; | |||
plot(tau, Qp(pick) - Qi(pick,:)*cos(omega(1:8)*tau)); | |||
set(gca,'Ydir','reverse') | |||
xlabel('\tau\rightarrow'); | |||
ylabel('w/w_s\rightarrow'); | |||
hold off; | |||
%% E - N - D | |||
</syntaxhighlight></td></tr></table> | |||
}} | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 7. November 2021, 16:49 Uhr
Aufgabenstellung
Analog zu FEAF untersuchen wir hier die Schwingungen eines Kontinuums beim Loslassen aus der entspannten Rugelage. Hier nicht mit einem Dehnstab, sondern einem Euler-Bernoulli-Balken.
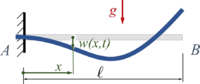
Gesucht ist die Schwingung eines Euler-Bernoulli-Balkens beim Loslassen aus der Ruhelage. Wir gehen nach dem Standardrezept der Finite Elemente Methode vor, arbeiten also mit dem Prinzip der virtuellen Arbeit.
Lösung mit Matlab®
Interessant ist hier, dass - im Gegensatz zu Stablängsschwingungen - die Eigenfrequenz nicht ein gerades Vielfaches der untersten Eigenfrequenz ist. Falls Sie ein Saiteninstrument spielen, verstehen Sie sofort, warum das wichtig ist.
Maxima können wir hier nicht gut gebrauchen: die Gleichungen werden zu umfangreich. Wir arbeiten also mehr mit numerischen Verfahren, da ist Matlab geeigneter.
Header
Im Programm arbeiten wir mit einer dimensionslosen Formulierung - wir brauchen dafür eine Bezugszeit tBez und eine Bezugslänge lBez.
Bezugsgrößen wählen
Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe SKEB):
|
Analytische Lösung: homohener Lösungsanteil |
Analytische Lösung: partikularer Lösungsanteil |
|---|---|
|
Die homogene Bewegungsgleichung des Euler-Bernoulli-Balkens hat Lösungen vom Typ Wir bekommen zu jedem ω0 vier κ Das α ist eine praktische Abkürzung, hinter der wir ω0 verstecken. Anders als beim Dehnstab (SKER) finden wir hier keine analytische Beziehung, sondern nur die numerischen Beziehungen, für die unsere Randbedingungen erfüllt sind: Die langsamste Eigenmode gehört zu α1 mit der Periodendauer
Also wählen wir . |
Die zugeordnete inhomogene Bewegungsgleichung des Euler-Bernoulli-Balkens hat die partikulare Lösung Die statische Auslenkung am unteren Ende ist demnach
Wir wählen . |
System-Parameter des FEM-Modells
Für die Diskretisierung wählen wir als Anzahl der Finiten Elemente (Number Of Elements):
und damit je Element
- .
Wir wählen die kubische Ansatzfunktionen aus dem Abschnitt Finite Elemente Methode je Element, also
Für die numerisch Implementierung stört in dieser Darstellung das Element-spezifische ℓi - die Elementlänge. Wir behelfen uns, indem wir die Ansatzfunktionen schreiben als
- ,
wobei wir die Ansatz-Polynome in verpacken.
Das schaut unnötig komplex aus - allerdings stecken wir die Diagonal-Matrizen d (für jedes Element eine) in eine Matlab®-Variable, so dass sie dort nicht weiter auffällt.
Die abhängigen Koordinaten des FEM-Modells sind dann zunächst - bis zum Einarbeiten der Randbedingungen - diese:
- .
Matlab
Classes
In dieser CODE-Sektion kommt ein Beispiele zum Aufbau des Matlab®-Programms mit Klassen (Objektbasierte Programmierung)
-
FEM-Section classdef FEM_Section % section section parameters properties rho; E; beta; h; b; l; end methods % Constructor function self = FEM_Section(parHashMap) self.rho = parHashMap('rho'); self.E = parHashMap('E'); self.beta = parHashMap('beta'); self.h = parHashMap('h'); self.b = parHashMap('b'); self.l = parHashMap('l'); end % end Constructor % start bending stiffness EI function EI = bendingStiffness(self) EI = self.E*1/12.*self.b*self.h^3; end % end bending stiffness % start cross-sectional area function A = cossecArea(self) A = self.b*self.h; end % end bending stiffness % start mass function m = mass(self) m = self.rho*self.b*self.h*self.l; end % end mass end end
-
FEM-Element-Model classdef FEM_Element_Modell % modell parameters properties type; % element type noe; % number of elements of this type noc; % number of coordinates per node phi; % trial-functions M; % element-mass matrix K; % element-stiffness matrix G; % element-load matrix (g) end methods % Constructor function self = FEM_Element_Modell(parHashMap) self.type = parHashMap('Type'); self.noe = parHashMap('NOE'); if self.type == 'EBB' % Euler-Bernoulli-Beam Elements self.phi = [[ 2,-3, 0, 1];... [ 1,-2, 1, 0];... [-2, 3, 0, 0];... [ 1,-1, 0, 0]]; self.noc = 2; elseif self.type == 'ER' % Extensible Rod type self.phi = [[-1, 1]; ... [ 1, 0]]; self.noc = 1; end [self.M,self.K,self.G] = self.ElementMassMatrix(); end % end Constructor function [M, K, G] = ElementMassMatrix(self) m = length(self.phi); M = zeros(m,m); K = zeros(m,m); G = zeros(m,1); for row = 1:m for col = 1:m M(row,col) = diff(... polyval(... polyint(... conv(self.phi(row,:),self.phi(col,:))),... [0,1])); if self.type == 'EBB' % -> second derivs K(row,col) = diff(... polyval(... polyint(... conv(polyder(polyder(self.phi(row,:))),polyder(polyder(self.phi(col,:))))),... [0,1])); elseif self.type == 'ER' % -> first derivs K(row,col) = diff(... polyval(... polyint(... conv(polyder(self.phi(row,:)),polyder(self.phi(col,:)))),... [0,1])); end end G(row,1) = diff(... polyval(... polyint(... self.phi(row,:)),... [0,1])); end end end end
-
FEM-Container classdef FEM_Container % holds all system matrics properties % matrices M; % mass matrix D; % damping matrix K; % stiffness matrix G; % gravitational Loading d; % scalting matrix with l[i]-Element % rod length l; % length % model properties NOE; % number of elements NON; % number of nodes NOC % number of coordinates per node NOQ % number of coordinates in total g; % 9.81 m/s^2 % boundary conditions free; disabled; % functions trials; % solution samples; % number of samples when plotting with points end methods % Constructor function self = FEM_Container(bezug,system,boundaries,element) % declarations NOE = sum(element.noe); % number of all elements in all sections NON = NOE+1; % number of nodes NOC = element.noc; % number of coordinates per node NOQ = NON*NOC; % number of coordintes self.NOE = NOE; self.NON = NON; self.NOC = NOC; self.NOQ = NOQ; % number of samples when plotting self. samples = 21; % global params self.g = 9.81/(bezug('l_ref')/bezug('t_ref')^2); % FE-lengths self.l = [0]; for sec = 1: length(system) for ele = 1: element.noe(sec) self.l = [self.l, self.l(length(self.l))+system(sec).l/element.noe(sec)]; end end % initialize system matrices [self.M, self.K, self.G, self.d] = self.systemMatrices(system, element); % collect boundary conditions free = linspace(1,1, element.noc*(sum(element.noe)+1)); touch = [1]; for sec = 1: length(element.noe) touch = [touch,touch(length(touch))+element.noc*element.noe(sec)]; end for i= 1:min(length(touch),length(boundaries)) nodeNo= touch(i); free(nodeNo:nodeNo+element.noc-1) = boundaries(i).free; end disabled = ~free; self.free = (1:length(free)).*free; self.free(self.free==0)=[]; disabled = (1:length(disabled)).*disabled; self.disabled = (1:length(disabled)).*disabled; self.disabled(self.disabled==0)=[]; % trial functions self.trials = element.phi; end % end Constructor % start system matrices function [M,K,G,d] = systemMatrices(self, system, element) M = zeros(self.NOQ,self.NOQ); K = zeros(self.NOQ,self.NOQ); G = zeros(self.NOQ, 1 ); d = zeros(4, 4, self.NOE ); g = self.g; e = 0;% counter for all elements of all sections for section = 1: length(element.noe) L = system(section).l/element.noe(section); m = system(section).rho*system(section).cossecArea()*L; % beinding stiffness b = system(section).bendingStiffness()/L^3; for i = 1:element.noe(section) e = e+1; if element.type=='EBB' d(:,:,e) = diag([1,L,1,L]); % diagnoal matrix with l[i]-factors elseif element.type=='ER' d(:,:,e) = diag([1,1]); end % j = 2*(e-1)+1; M(j:j+3,j:j+3) = M(j:j+3,j:j+3)+m* d(:,:,e)*element.M*d(:,:,e); K(j:j+3,j:j+3) = K(j:j+3,j:j+3)+b* d(:,:,e)*element.K*d(:,:,e); G(j:j+3,1) = G(j:j+3,1) +m*g*d(:,:,e)*element.G; end end end % end system matrices % start boudaryconditions function [M,K,G] = constrained(self) M = self.M(self.free,self.free); K = self.K(self.free,self.free); G = self.G(self.free, 1 ); end % end system matrices % start eigensystem function [V,D] = eigensystem(self) % ODE: A q + B q = 0 % = - = - - % define system matrices [A,B,G] = self.constrained(); %S = linsolve(A,-B); S = inv(A)*(-B); % eigensystem [V,D] = eig(S); end % end eigensystem % start particular solution function Q = particularSolution(self) % ODE: A q + B q = G % = - = - - % define system matrices [A,B,G] = self.constrained(); Q = linsolve(B,G); end % end particular solution end end
Eingabe-Parameter aus Excel
 |
 |
 |
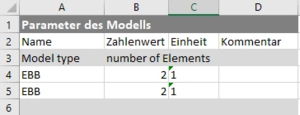 |
Equilibrium Conditions
Die Gleichgewichtsbedingung mit dem Prinzip der virtuellen Verrückungen setzen sich additiv aus
- ,
zusammen - also den virtuellen Arbeiten je Element zuzüglich von virtuellen Arbeiten am Rand. In unserem Beispiel haben wir allerdings keine eingeprägten, äußeren Lasten am Rand, also ist
- .
Je Element erfassen wir die virtuellen Arbeiten durch Element-Matrizen. So ist z.B. für die virtuelle Formänderungsenergie (vgl. Finite Elemente Methode)
mit der Element-Steifigkeitsmatrix .
Aus der FEM-Formulierung für den Euler-Bernoulli-Balken könnten wir die Element-Matrizen der virtuellen Arbeit der D'Alembert'schen Trägheitskraft sowie der Virtuelle Formänderungsenergie herauskopieren. Auch die "rechte Seite" mit der virtuelle Arbeit der Gewichtskraft aus
- ,
könnten wir als Element-Lastmatrix (Spaltenmatrix) abspeichern.
- .
Dass es auch anders geht,sehen Sie in der Definition der Matlab®-Klasse FEM_Element_Modell, bei der die Element direkt aus den Trial-Functions - hier den -
hergeleitet. werden:
:
K(row,col) = diff(...
polyval(...
polyint(...
conv(polyder(self.phi(row,:)),polyder(self.phi(col,:)))),...
[0,1]));
:
Komponieren der System-Matrizen
Die System-Matrizen des Gesamt–Systems komponieren wir nun durch Hinzuaddieren der Anteile je Element.
Beispiel: die Gesamt-Steifigkeitsmatrix für I=2:
Die Beiträge der zwei Elemente sind hier in rot bzw. grün eingefärbt.
Dieses "Hinzuaddieren" passiert in Matlab hier:
:
e = 0;% counter for all elements of all sections
for section = 1: length(element.noe)
:
for i = 1:element.noe(section)
e = e+1;
:
j = 2*(e-1)+1;
:
K(j:j+3,j:j+3) = K(j:j+3,j:j+3)+b* d(:,:,e)*element.K*d(:,:,e);
:
end
:
In Matrix-Schreibweise lautet die Bewegungsgleichung des Gesamt-Systems jetzt:
- .
Einarbeiten der Randbedingungen
Die Randbedingungen arbeiten wir ein, indem wir zeilenweise (für δW und δΦ) und spaltenweise (für W und Φ) streichen.
Hier sind es
- die erste Zeile/Spalte für W0 (blau) und
- die zweite Zeile / Spalte für Φ0 (grün).
NONE - see below
Solving
Die Lösung des Anfangs- und Randwertproblems ist in diesem Lösungsansatz mit Matlab® um die Klasse "FEM_Container" herum aufgebaut - in ihr sind alle Parameter und Lösungsprozesse beschrieben.
Hier heißt die Instanz des Modells
- mathModel
In diesem Container sind alle Parameter und Zustandsgrößen des Modells bereits dimensionslos gemacht - und zwar mit den oben genannten Bezugsgrößen, die in der Excel-Eingabedatei im Blatt "0) Bezugsgrößen" definiert sind.
Die Lösung des Anfangswertproblems setzt sich aus zwei Teilen zusammen:
- der partikularen Lösung, die die Rechte Seite "G" erfüllt und
- der homogenen Lösung, die die Rechte Seite "0" erfüllt.
Die Gesamtlösung Qt setzt sich nun - bei diesem linearen System - additiv aus partikularer Qp und Qh homogener Lösung zusammen:
Particular Solution
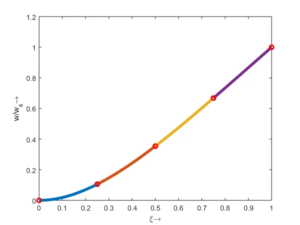
Die rechte Seite der Bewegungsgleichung G ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung Qp statisch, wir suchen nach der Lösung des Gleichungssystems
und die ist - mit der Normierung durch ws -
>> Qp
Qp =
0
0
0.1055
0.0042
0.3542
0.0064
0.6680
0.0072
1.0000
0.0073
Diese Lösung tragen wir - elementweise - auf.
Homogene Lösung
Zur Lösung der homogenen Bewegungsgleichung
setzen wir an
und erhalten das Eigenwertproblem
mit
| den Eigenwerten | und |
| den Egenvektoren | . |
Für die Berechnung der Eigenwerte λ müssen wir die Abkürzung
einführen. Damit arbeitet die Matlab®-Routine "eig()", die in "mathModel.eigensystem()" implementiert ist.
Acht Eigenwerte kommen aus der Bedingung , diese werden auf der Spur der Matrix D abgelegt:
>> D
D =
1.0e+06 *
-2.9006 0 0 0 0 0 0 0
0 -1.0774 0 0 0 0 0 0
0 0 -0.4287 0 0 0 0 0
0 0 0 -0.1662 0 0 0 0
0 0 0 0 -0.0480 0 0 0
0 0 0 0 0 -0.0123 0 0
0 0 0 0 0 0 -0.0016 0
0 0 0 0 0 0 0 -0.0000
Die zugehörigen dimensionslosen Periodendauern sind
- .
Und offensichtlich fällt die längste Periodendauer T8 mit der analytisch berechneten untersten Schwingunsperiode T* zusammen.
Die zugehörigen Eigenvektoren stehen in V:
>> V
V =
-0.0579 0.2951 -0.0687 0.3043 0.4561 0.5309 -0.3197 -0.0780
-0.0129 0.0882 -0.0805 -0.0578 -0.0115 0.0064 -0.0096 -0.0032
-0.0884 -0.1020 0.4873 -0.0417 -0.4707 0.0160 -0.5469 -0.2721
-0.0364 0.1230 0.0134 0.0659 -0.0007 -0.0222 0.0019 -0.0051
-0.1652 -0.4100 -0.2420 -0.1979 0.4058 -0.4268 -0.1035 -0.5270
-0.0763 0.0330 0.0704 -0.0601 0.0098 0.0106 0.0163 -0.0059
-0.9540 -0.8313 -0.8232 0.9212 -0.6357 0.7308 0.7663 -0.8013
-0.2099 -0.1390 -0.0999 0.0809 -0.0389 0.0315 0.0200 -0.0060
Die Eigenvektoren in V spannen nun den Nullraum (nullspace) der Matrix auf, es ist
Die homogene Lösung der Bewegungsgleichung lautet damit
mit den acht Integrationskonstanten Ci . Durch die komplexen Eigenwerte sind die Integrationskonstanten nun (eigentlich) auch komplexwertig. Darum kommen in diesem Fall herum, weil die Anfangsgeschwindigkeit des Balkens beim Loslassen Null ist - wir also nur cos-Anteile berücksichtigen müssen. Und die gehören wiederum zum Realteil der Exponential-Funktion.
Die Ci sind nun die Konstanten, die wir brauchen, um die Lösung an Anfangsbedingungen anzupassen.
Vorher schauen wir uns die Lösung jeweils zu einer Eigenfrequenz ωi an. Diese Funktionen heißen Modalformen ϕ(x) und deren Schwingungen können wir plotten:
| Mode | Modalform ϕj(x) | Mode | Modalform ϕj(x) |
|---|---|---|---|
| #8 |
 |
#7 |
 |
| #6 |
 |
#5 |
 |
| #4 |
 |
#3 |
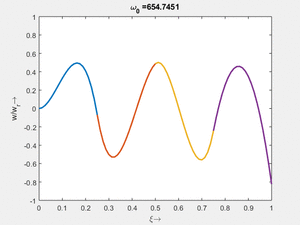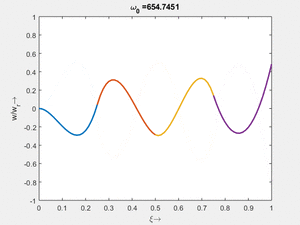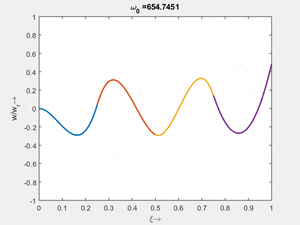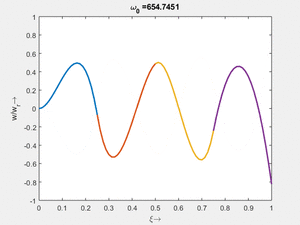 |
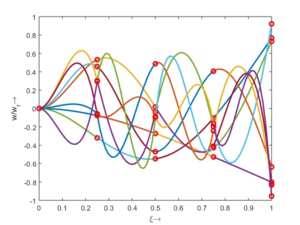
Alle acht Moden ϕj können wir auch zum Zeitpunkt τ=0 übereinander darstellen:
| ✔ Zur Euler-Bernoulli-Hypothese: |
| Praktisch haben die höheren Moden kaum Relevanz - meist klingen sie durch Dämpfung schnell ab. Man sieht allerdings bereits an der Schwingungs-Form, dass hier die Länge zwischen zwei Knoten nicht mehr sehr klein ist im Vergleich zur Höhe. Und das führt dazu, dass Schubverformungen eine Rolle spielen. Wir müssen zum Timoshenko-Balken wechseln .... |
Matlab®
Main Script
| Main - part I (preprocessor) |
|---|
% DESCRIPTION
% _____________________________________
% computes solutions for straight rods
% reads parameters from
% FEAG.xlsx
% writes results to
% feag-*.gif
% feag-*.png
% process
% uses own functions
% - readSystemParameters(fileName);
% - getUnitConversion
% -
% uses classes
% - FEM_Container
% - FEM_Element_Modell
% - FEM_Section
% - FEM_BoundaryCondition
% uses MATLAB functions
% - linsolve
% - eig
cd('C:\Users\abs384\OneDrive\Confluence Sources\FEAG');
addpath(['../Matlab/Functions']);
addpath(['../Matlab/Classes']);
%%****************************************
% PREPROCESSOR *
% ****************************************
fileName = 'FEAG';
[ bezug, system, boundaries, element, err ] = readSystemParameters(fileName);
%%
mathModel = FEM_Container(bezug,system,boundaries,element);
%%
:
:
:
|
| Main - part II (partikulare Lösung) |
|---|
:
:
:
%% ***************************************************************************/
% p a r t i c u l a r s o l u t i o n */
% ***************************************************************************/
NOV = length(mathModel.free)+length(mathModel.disabled);
% initiate particular solution Qp
Qp = zeros(NOV,1);
Q = mathModel.particularSolution();
Qp(mathModel.free,:)=Q;
% get coordinates of nodes
L = mathModel.l(length(mathModel.l));
% plot particular solution
for ele= 1: mathModel.NOE
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples);
plot(xi,Qp(2*ele-1:2*ele+2,1)'*(mathModel.d(:,:,ele)*phi), 'LineWidth',4); hold on;
end
plot(mathModel.l/mathModel.l(length(mathModel.l)),Qp(1:2:length(Qp)),'ro', 'LineWidth',2);
xlabel('\xi\rightarrow');
ylabel('w/w_s\rightarrow');
hold off;
|
| Main - part III (homogene Lösung) |
|---|
:
:
:
%% ***************************************************************************/
% * h o m o g e n e o u s s o l u t i o n */
% ***************************************************************************/
[V,D] =mathModel.eigensystem();
% eigenfrequencies of system
omega = sqrt(diag(-D));
Qh = zeros(NOV,length(mathModel.free));
Qh(mathModel.free,:) = V(:,:);
% plot modes
for mode =length(mathModel.free):-1:1
for ele= 1: mathModel.NOE
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples);
plot(xi,Qh(2*ele-1:2*ele+2,mode)'*(mathModel.d(:,:,ele)*phi), 'LineWidth',2); hold on;
end
plot(mathModel.l/mathModel.l(length(mathModel.l)),Qh(1:2:length(Qp),mode),'ro', 'LineWidth',2);
xlabel('\xi\rightarrow');
ylabel('w/w_r\rightarrow');
end
hold off;
|
Adapt to Initial Conditions
Die acht reell-wertigen Integrationskonstanten Ci bestimmen wir aus den Anfangsbedingungen für den Balken, nämlich
- ,
also
- .
Wenn wir die Ci komplexwertig denken, so stehen hier 16 Anfangsbedingungen für acht komplexe Ci .
Denken wir die Ci gleich reelwertig, so können wir die acht Anfangsbedingungen in der rechten Spalte weglassen - sie sind dann implizit mit erfüllt - für unser spezielles Anfangswertproblem.
Die Anfangsbedingung für die Gesamtlösung lautet nun:
- ,
also
Wir finden
- .
und damit
- .
Offensichtlich ist der Beitrag der Mode 8 (also der langsamsten Mode) bei weitem am größten Anteil an Qh. Das können wir auch in der Animation der Lösung - also das Loslassen des Balken aus der Ruhe heraus - sehen.
Matlab®
Main Script
| Main - part IV (adapt to initial conditions) |
|---|
:
:
:
%% ***************************************************************************/
% t o t a l ( c o m p o s e d ) s o l u t i o n */
% ***************************************************************************/
C = linsolve(Qh(mathModel.free,:),Qp(mathModel.free,1));
Qi = zeros(NOV,length(mathModel.free));
Qi(mathModel.free,:) = Qh(mathModel.free,:)*diag(C);
for ele= 1: mathModel.NOE
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples);
plot(xi,Qp(2*ele-1:2*ele+2,1)'*(mathModel.d(:,:,ele)*phi), 'Color', [0.8 0.8 0.8], 'LineWidth',8); hold on;
end
for mode =1 : length(mathModel.free)
for ele= 1: mathModel.NOE
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples);
plot(xi,Qi(2*ele-1:2*ele+2,mode)'*(mathModel.d(:,:,ele)*phi), 'LineWidth',2); hold on;
end
end
hold off;
|
Post-Processing
Die FEM-Lösung im Zeitbereich, angepasst an die Anfangsbedingungen, sieht nun so aus:
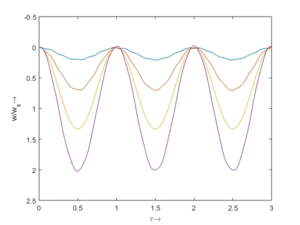 |
 |
Matlab®
Main Script
| Main - part IV (adapt to initial conditions) |
|---|
:
:
:
%% animated shape ....
tau = linspace(0,3,3*21);
h = figure;
axis tight manual % this ensures that getframe() returns a consistent size
fileName = strcat('feag-initial-value-solution-animation.gif');
for step = tau
hold off;
for ele= 1: mathModel.NOE
xi = linspace(mathModel.l(ele)/L,mathModel.l(ele+1)/L,mathModel.samples);
disp = Qp(2*ele-1:2*ele+2,1)'*(mathModel.d(:,:,ele)*phi);
for mode =length(mathModel.free):-1:1
disp = disp - Qi(2*ele-1:2*ele+2,mode)'*(mathModel.d(:,:,ele)*phi)*cos(2*pi*omega(mode)/omega(length(omega))*step);
end
plot(xi,disp, 'LineWidth',2); hold on;
axis([0 1 -0.1 2.1]);
set(gca,'Ydir','reverse')
xlabel('\xi\rightarrow');
ylabel('w/w_r\rightarrow');
end
title('initial value solution');
drawnow
% Capture the plot as an image
frame = getframe(h);
im = frame2im(frame);
[imind,cm] = rgb2ind(im,256);
% Write to the GIF File
if step == 0
imwrite(imind,cm,fileName,'gif', 'Loopcount',inf,'DelayTime',0);
else
imwrite(imind,cm,fileName,'gif','WriteMode','append','DelayTime',0);
end
end
hold off;
%% time domain ....
tau = linspace(0,3,3*71);
fileName = 'feag-initial-value-solution-W.gif';
pick = 3:2:mathModel.NOQ;
plot(tau, Qp(pick) - Qi(pick,:)*cos(omega(1:8)*tau));
set(gca,'Ydir','reverse')
xlabel('\tau\rightarrow');
ylabel('w/w_s\rightarrow');
hold off;
%% E - N - D
|
Links
- ...
Literature
- ...