Sources/Lexikon/Vektor: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
Vektoren stellen wir dar durch einen Pfeil und eine Maßzahl (hier ''F''). | Vektoren stellen wir dar durch einen Pfeil und eine Maßzahl (hier ''F''). | ||
<table style="background-color:white; margin-right:14px;"> | |||
<tr><th>Vektor</th><th>=</th><th>Pfeil</th><th>+</th><th>Maßzahl</th></tr> | |||
<tr><td>[[Datei:Vektor-01.png|alternativtext=|rahmenlos|93x93px]]</td><td></td><td>Richtung mit<br/>Orientierung<br/>(Richtungssinn)</td><td></td><td>Größe</td></tr> | |||
</table> | |||
Die Mathematik bezeichnet auch Spaltenmatrizen (vgl. [[Werkzeuge/Lösungsbausteine der Mathematik/Gewöhnliche lineare Gleichungssysteme|Gewöhnliche lineare Gleichungssysteme]]) als Vektoren. Für uns Ingenieure ist dieser Begriff durch die physikalische Bedeutung einer gerichteten und orientierten Größe im Raum besetzt. | Die Mathematik bezeichnet auch Spaltenmatrizen (vgl. [[Werkzeuge/Lösungsbausteine der Mathematik/Gewöhnliche lineare Gleichungssysteme|Gewöhnliche lineare Gleichungssysteme]]) als Vektoren. Für uns Ingenieure ist dieser Begriff durch die physikalische Bedeutung einer gerichteten und orientierten Größe im Raum besetzt. | ||
Den Pfeil erfassen wir in Rechnungen der Mechanik durch den Einheitsvektor | Den Pfeil erfassen wir in Rechnungen der Mechanik durch den Einheitsvektor | ||
<math>\vec{e}</math>. | ::<math>\vec{e}</math>. | ||
Einheitsvektoren in bestimmte Raumrichtungen kennzeichnen wir durch die unabhängige Koordinate der Raumrichtung, also | Einheitsvektoren in bestimmte Raumrichtungen kennzeichnen wir durch die unabhängige Koordinate der Raumrichtung, also | ||
<math>\vec{e}_x, \; \vec{e}_y, \; \vec{e}_z.</math>. | ::<math>\vec{e}_x, \; \vec{e}_y, \; \vec{e}_z.</math>. | ||
Und diese drei fassen wir zu einer Spaltenmatrix | Und diese drei fassen wir zu einer Spaltenmatrix | ||
<math>\vec{\underline{e}} = \left(\begin{array}{c}\vec{e}_x\\\vec{e}_y\\\vec{e}_z \end{array}\right)</math> | ::<math>\vec{\underline{e}} = \left(\begin{array}{c}\vec{e}_x\\\vec{e}_y\\\vec{e}_z \end{array}\right)</math> | ||
zusammen. | zusammen. | ||
| Zeile 29: | Zeile 33: | ||
Bei kartesischen Koordinatensystemen fallen die Koeffizienten der Einheitsvektoren mit den Komponenten der Vektoren zusammen, z.B. beim Raumvektor | Bei kartesischen Koordinatensystemen fallen die Koeffizienten der Einheitsvektoren mit den Komponenten der Vektoren zusammen, z.B. beim Raumvektor | ||
<math>\vec{r} = \vec{\underline{e}}^T\cdot\underbrace{\left(\begin{array}{l}r_x\\r_y \\ r_z \end{array}\right)}_{\displaystyle := \underline{r}}</math>. | ::<math>\vec{r} = \vec{\underline{e}}^T\cdot\underbrace{\left(\begin{array}{l}r_x\\r_y \\ r_z \end{array}\right)}_{\displaystyle := \underline{r}}</math>. | ||
Das das nur für diesen Sonderfall funktioniert, sehen Sie sofort bei [[Sources/Lexikon/Unabhängige Koordinaten|Kugel-Koordinaten]]. | Das das nur für diesen Sonderfall funktioniert, sehen Sie sofort bei [[Sources/Lexikon/Unabhängige Koordinaten|Kugel-Koordinaten]]. | ||
Aktuelle Version vom 21. April 2021, 15:36 Uhr
Viele physikalische Größen haben Vektor-Charakter, wie z.B.
- eine Kraft
- eine Spannung
- ein Ort im Raum bezüglich eines Referenzpuntkes
- eine Geschwindigkeit.
Vektoren sind gerichtete und Raum orientierte Größen.
Vektoren stellen wir dar durch einen Pfeil und eine Maßzahl (hier F).
| Vektor | = | Pfeil | + | Maßzahl |
|---|---|---|---|---|
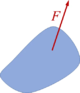 | Richtung mit Orientierung (Richtungssinn) | Größe |
Die Mathematik bezeichnet auch Spaltenmatrizen (vgl. Gewöhnliche lineare Gleichungssysteme) als Vektoren. Für uns Ingenieure ist dieser Begriff durch die physikalische Bedeutung einer gerichteten und orientierten Größe im Raum besetzt.
Den Pfeil erfassen wir in Rechnungen der Mechanik durch den Einheitsvektor
- .
Einheitsvektoren in bestimmte Raumrichtungen kennzeichnen wir durch die unabhängige Koordinate der Raumrichtung, also
- .
Und diese drei fassen wir zu einer Spaltenmatrix
zusammen.
Bei kartesischen Koordinatensystemen fallen die Koeffizienten der Einheitsvektoren mit den Komponenten der Vektoren zusammen, z.B. beim Raumvektor
- .
Das das nur für diesen Sonderfall funktioniert, sehen Sie sofort bei Kugel-Koordinaten.