Gelöste Aufgaben/UEBP: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:EBB-load-case-05.png|alternativtext=|links|200px|Lageplan]] | [[Datei:EBB-load-case-05.png|alternativtext=|mini|links|200px|Lageplan]] | ||
Gesucht ist eine Lösung für die Biegelinie mit dem [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Verfahren von Rayleigh-Ritz (EBB)|Ansatz von Ritz]] und zwei Trial-Funktionen. | Gesucht ist eine Lösung für die Biegelinie mit dem [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Verfahren von Rayleigh-Ritz (EBB)|Ansatz von Ritz]] und zwei Trial-Funktionen. | ||
</onlyinclude> | </onlyinclude> | ||
| Zeile 29: | Zeile 29: | ||
* Ansatzfunktionen über die gesamte Länge des Balkens arbeiten wir | * Ansatzfunktionen über die gesamte Länge des Balkens arbeiten wir | ||
* hier mit zwei Finiten Elementen (Sektionen), für die wir separat ansetzen. | * hier mit zwei Finiten Elementen (Sektionen), für die wir separat ansetzen. | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text= | ||
Wir berechnen die Potentielle Energie '''U''' des Systems in Abhängigkeit von den generalisierten Koordinaten Wi und erhalten aus | |||
::<math>\displaystyle \frac{d\,U}{d\,W_i} \stackrel{!}{=} 0 </math> | |||
die Gleichung für den gesuchten Koeffizienten Wi der Trial-Funktionen. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2019-10-19 */ | |||
/* ref: TMC, Labor 3 */ | |||
/* description: Ritz / FEM approach to EBB, load-case 5*/ | |||
/* */ | |||
/*******************************************************/ | |||
/* declare variables and functions */ | |||
declare("Π", alphabetic); /* strain energy */ | |||
declare("ℓ", alphabetic); | |||
assume(ℓ>0); | |||
dimless:[x=xi*ℓ, | |||
a=alpha*ℓ]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }}<!--------------------------------------------------------------------------------> | ||
== | {{MyCodeBlock|title=Declarations | ||
|text= | |||
Um die Lösung dimensionslos zu machen, nutzen wir wieder die [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Einzelmoment, doppeltgelenkige Lagerung|analytische Lösung des Problems]] und | Um die Lösung dimensionslos zu machen, nutzen wir wieder die [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Einzelmoment, doppeltgelenkige Lagerung|analytische Lösung des Problems]] und | ||
| Zeile 48: | Zeile 66: | ||
Dimensionslose Orts-Koordinaten sind | Dimensionslose Orts-Koordinaten sind | ||
<math>\begin{array}{ll} x &= \xi\cdot \ell,\\ a &= \alpha\cdot \ell. \end{array}</math>. | ::<math>\begin{array}{ll} x &= \xi\cdot \ell,\\ a &= \alpha\cdot \ell. \end{array}</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*********************************************************/ | |||
/*analytic solution vgl. Euler-Bernoulli-Blaken/Standard-Lösungen#case5*/ | |||
analytic: w(xi) = M*ℓ^2/(6*EI)*(xi^3+xi*(2-6*alpha+3*alpha^2) | |||
/* foeppel-function */ | |||
- 3*(if xi<alpha then 0 else xi-alpha)^2); | |||
W[max] : M*ℓ^2/(9*sqrt(3)*EI); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | |||
|text= | |||
Dass wir in [[Gelöste Aufgaben/UEBO|UEBO]] die Trial-Funktions ''ϕ'' über die gesamte Stablänge angesetzt haben, führt bei den berechneten Näherungen für die Momente ''M(x)'' und letztlich auch für die Verschiebungen ''w(x)'' zu massiven Fehlern. Einen Sprung in der Momenten-Kennlinie mit einem Polynom zu approximieren, geht halt nicht gut. | Dass wir in [[Gelöste Aufgaben/UEBO|UEBO]] die Trial-Funktions ''ϕ'' über die gesamte Stablänge angesetzt haben, führt bei den berechneten Näherungen für die Momente ''M(x)'' und letztlich auch für die Verschiebungen ''w(x)'' zu massiven Fehlern. Einen Sprung in der Momenten-Kennlinie mit einem Polynom zu approximieren, geht halt nicht gut. | ||
Ein Schritt hin zur Methode der Finiten Elemente ist bei diesem "modifizierten Verfahren von Rayleigh-Ritz" der Ansatz der Trial-Functions in zwei Sektionen - also wie bei analytischen Lösung auch. | Ein Schritt hin zur [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten Elemente]] ist bei diesem "modifizierten Verfahren von Rayleigh-Ritz" der Ansatz der Trial-Functions in zwei Sektionen - also wie bei analytischen Lösung auch. | ||
Die Sektions- (Element-) Längen sind dabei | Die Sektions- (Element-) Längen sind dabei | ||
| Zeile 68: | Zeile 89: | ||
* für Sektion I: <math>\ell_I = \alpha \cdot \ell</math> und | * für Sektion I: <math>\ell_I = \alpha \cdot \ell</math> und | ||
* für Sektion II: <math>\ell_{II} = (1-\alpha) \cdot \ell</math>. | * für Sektion II: <math>\ell_{II} = (1-\alpha) \cdot \ell</math>. | ||
[[Datei:UEBP-11.png|alternativtext=|mini|200px|Unabhängige Koordinaten der Finiten Elemente]] | |||
Und wir arbeiten mit je einer Ortskoordinate ''ξ<sub>i</sub>'' je Sektion, also | |||
::<math>0 \le \ell_I \cdot \xi_I < a \text{ und } 0 \le \ell_{II} \cdot \xi_{II} < \ell-a</math> | |||
mit | |||
::<math>0 \le \xi_i < 1</math> | |||
Für die Trial-Functions wählen wir sektionsweise Polynome zweiten Grades | |||
::<math>\begin{array}{lcl} | |||
w_{I }(\xi_I ) &=& c_{1,2}\cdot \xi^2+c_{1,1}\cdot \xi+c_{1,0}\\ | |||
w_{II}(\xi_{II)} &=& c_{2,2}\cdot \xi^2+c_{2,1}\cdot \xi+c_{2,0} | |||
\end{array}</math>, | |||
< | deren Koeffizienten ''c<sub>ij</sub>'' wir nun an die geometrischen Randbedingungen anpassen müssen: | ||
::<math>\begin{array}{lcl} | |||
w_I(0) &=& 0\\ | |||
w_I(1) &=& w_{II}(0)\\ | |||
\left.\displaystyle \frac{d w_I(\xi_I)}{d x}\right|_{\xi=1} &=& \left.\displaystyle \frac{d w_{II}(\xi_{II})}{d x}\right|_{\xi=0}\\ | |||
w_{II}(1) &=& 0\\ | |||
\end{array}</math> | |||
Zusätzlich ersetzen wir zwei ''c<sub>ij</sub>'' durch die Verschiebung und Verdrehung im Momenten-Einleitungspunkt | |||
::<math>\begin{array}{lcl} | |||
W &:=& w_{II}(0)\\ | |||
\Phi &:=& \left.\displaystyle \frac{d w_{II}(\xi_{II})}{dx}\right|_{\xi=0} | |||
\end{array}</math>, | |||
so dass die Trial-Functions die Form | |||
::<math>w(x) = \left\{\begin{array}{ccl} | |||
W \cdot \phi_{1,1}(\xi_I) & + \Phi \cdot \phi_{1,2}(\xi_I) & \text{ für Sektion I}\\ | |||
W \cdot \phi_{2,1}(\xi_{II}) & + \Phi \cdot \phi_{2,2}(\xi_{II}) & \text{ für Sektion II} | |||
\end{array}\right.</math> | |||
annehmen bzw. | |||
::<math>w(x) = \left\{ \begin{array}{ccccl} | |||
W & \cdot \left(2\cdot \xi_{I}-{{\xi_{I}}^{2}}\right) &+ | |||
\Phi &\cdot \left( \alpha\cdot {{\xi_{I}}^{2}}-\alpha\cdot \xi_{I}\right) \cdot \ell & \text{ für } 0 < x < a,\\ | |||
W &\cdot \left(1-{{\xi_{II}}^{2}}\right) &+ | |||
\Phi &\cdot \left( \left( \alpha-1\right) \cdot {{\xi_{II}}^{2}}+\left( 1-\alpha\right) \cdot \xi_{II}\right) \cdot \ell & \text{ für } a < x < \ell. | |||
\end{array}\right.</math> | |||
Im Plot sehen die vier Funktionen (zwei je Sektion, zwei Sektionen) so aus: | |||
| | [[Datei:UEBP-12.png|ohne|mini|Trial-Functions - wie bei der Methode der Finiten Elemente]] | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*********************************************************/ | ||
/* declare trial-function(s) */ | |||
ell : [alpha*ℓ,(1-alpha)*ℓ]; | |||
phi : makelist(sum(c[i,j]*xi^j,j,0,2),i,1,2); | |||
/*********************************************************/ | |||
/* boundary-conditions for geometric boundary conditions */ | |||
GBC: [subst([xi = 0 ], phi[1] ) = 0, | |||
subst([xi = 1 ], phi[1] ) = subst([xi = 0 ], phi[2] ), | |||
subst([xi = 1 ], phi[1] ) = W, | |||
subst([xi = 1 ], diff(phi[1],xi)/ell[1]) = Phi, | |||
subst([xi = 1 ], diff(phi[1],xi)/ell[1]) = subst([xi = 0 ], diff(phi[2],xi)/ell[2]), | |||
subst([xi = 1 ], phi[2] ) = 0]; | |||
sol[1] : solve(GBC,[c[1,0],c[2,0],c[1,1],c[2,1],c[1,2],c[2,2]])[1]; | |||
phi: expand(ratsimp(subst(sol[1],phi))); | |||
phi : ratsimp(makelist(makelist(coeff(phi[i],[W,Phi][j]),j,1,2),i,1,2)); | |||
/*********************************************************/ | |||
toPlot : [[parametric, alpha *t, phi[1][1] , [t,0,1]], | |||
[parametric, alpha *t, phi[1][2]/ℓ, [t,0,1]], | |||
[parametric, alpha+(1-alpha)*t, phi[2][1] , [t,0,1]], | |||
[parametric, alpha+(1-alpha)*t, phi[2][2]/ℓ, [t,0,1]]]; | |||
toPlot : subst([xi=t, alpha=6/10], toPlot); | |||
preamble: "set yrange [] reverse"; | |||
plot2d(toPlot, [y,-0.4,1], | |||
[legend, "ϕ11 ","ϕ12/ℓ1","ϕ21 ","ϕ22/ℓ2"], | |||
[gnuplot_preamble, preamble], | |||
[title, "trial-functions für α=6/10"], | |||
[xlabel, "x/ℓ →"], | |||
[ylabel, "<- ϕ"] ); | |||
ansatz: makelist(w[i](xi) = sum(phi[i][j]*[W,Phi][j],j,1,2),i,1,2); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Potential Energy | {{MyCodeBlock|title=Potential Energy | ||
|text= | |text= | ||
Für die Gleichgewichtsbedingungen setzten wir ''Π'' (aus Abschnitt Euler-Bernoulli-Balken) und ''A'' in ''U'' ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir | |||
::<math>\displaystyle \frac{d\phi}{x} = \frac{d\phi}{\xi_i}\cdot\underbrace{\displaystyle\frac{d\xi_i}{x}}_{\displaystyle = \frac{1}{\ell_i}}</math> | |||
berücksichtigen und erhalten mit der Arbeitsfunktion des Moments | |||
::<math>A = M \cdot w'|_{\displaystyle x=a}</math> | |||
das Potential in Matrix-Schreibweise: | |||
::<math>U = \displaystyle \frac{1}{2} \cdot \displaystyle \underline{Q}^T \cdot \underline{\underline{A}}\cdot \underline{Q} - \underline{Q}^T\cdot \underline{b} </math>. | |||
wobei | |||
::<math>\underline{Q} = \left(\begin{array}{c}W\\ \Phi\end{array}\right)</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /*********************************************************/ | ||
/* define potential energy of system */ | |||
PMPE : [U = Π - A, | |||
Π = sum(1/2*EI/ell[i]^3*'integrate('diff(w[i](xi),xi,2)^2,xi,0,1),i,1,2), | |||
A = M*Phi]; | |||
PMPE: subst(ansatz, subst(PMPE[3],subst(PMPE[2], PMPE[1]))); | |||
PMPE : expand(ev(PMPE,nouns)); | |||
/* unknowns */ | |||
Q : [W,Phi]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text= | |text= | ||
Diese Gleichung erfüllt die Gleichgewichtsbedingungen | |||
::<math>\displaystyle \frac{dU}{dQ_i} \stackrel{!}{=} 0</math>, | |||
wenn | |||
::<math>\begin{pmatrix}-\frac{\left( 4-12\cdot \alpha+12\cdot {{\alpha}^{2}}\right) \cdot EI}{\left( {{\alpha}^{6}}-3\cdot {{\alpha}^{5}}+3\cdot {{\alpha}^{4}}-{{\alpha}^{3}}\right) \cdot {{\ell}^{3}}} & \frac{4 \left( 2\cdot \alpha-1\right) \cdot EI}{\left( {{\alpha}^{4}}-2\cdot {{\alpha}^{3}}+{{\alpha}^{2}}\right) \cdot {{\ell}^{2}}}\\ 4 \frac{\left( 2\cdot \alpha-1\right) \cdot EI}{\left( {{\alpha}^{4}}-2\cdot {{\alpha}^{3}}+{{\alpha}^{2}}\right) \cdot {{\ell}^{2}}} & -\frac{4\cdot EI}{\left( {{\alpha}^{2}}-\alpha\right) \cdot \ell}\end{pmatrix}\cdot \begin{pmatrix}W\\ \Phi\end{pmatrix}=\begin{pmatrix}0\\ M\end{pmatrix} | |||
</math>. | |||
Hier kann man schon am Gleichungssystem ablesen, was für ''α=½'' passiert: dann werden die Nebendiagonal-Elemente mit Ihren ''(2 α-1)''-Koeffizienten zu Null, dann ist | |||
* <math>W = 0</math> und | |||
* <math>\displaystyle \frac{16 EI}{\ell} \Phi = M</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* equilibrium condition */ | ||
eom : makelist(expand(diff(subst(PMPE,U),Q[i])),i,1,2); | |||
A : funmake('matrix, makelist(makelist(coeff(eom[i],Q[j]),j,1,2),i,1,2)); | |||
b : - funmake('matrix, makelist([subst(makelist(Q[j]=0,j,1,2),eom[i])],i,1,2)); | |||
print(A,"∙",transpose(Q),"=",b)$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text= | |text= | ||
Auflösen der Gleichungen nach den unbekannten Koordinaten ''W'' und ''Φ'' liefert | |||
::<math>\begin{array}{ll} | |||
W & = \displaystyle \frac{\left( \alpha-3\cdot {{\alpha}^{2}}+2\cdot {{\alpha}^{3}}\right) \cdot M\cdot {{\ell}^{2}}}{4\cdot EI} \\ | |||
\Phi & = \displaystyle \frac{\left( 1-3\cdot \alpha+3\cdot {{\alpha}^{2}}\right) \cdot M\cdot \ell}{4\cdot EI} | |||
\end{array}</math>. | |||
Damit ist die gesuchte Näherungs-Lösung | |||
::<math>\begin{array}{ll} | |||
w_I( \xi_I) &= \frac{\left( \left( {{\alpha}^{3}}-3\cdot {{\alpha}^{2}}+\alpha\right) \cdot \xi+{{\alpha}^{3}}\cdot {{\xi}^{2}}\right) \cdot M\cdot {{\ell}^{2}}}{4\cdot EI}\\ | |||
w_{II}(\xi_{II}) &= \frac{\left( \alpha-3\cdot {{\alpha}^{2}}+2\cdot {{\alpha}^{3}}+\left( -3\cdot {{\alpha}^{3}}+6\cdot {{\alpha}^{2}}-4\cdot \alpha+1\right) \cdot \xi+\left( {{\alpha}^{3}}-3\cdot {{\alpha}^{2}}+3\cdot \alpha-1\right) \cdot {{\xi}^{2}}\right) \cdot M\cdot {{\ell}^{2}}}{4\cdot EI} | |||
\end{array}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /*********************************************************/ | ||
/* solve */ | |||
sol[2] : ratsimp(solve(eom,Q))[1]; | |||
/* approximated solution */ | |||
ritz : ratsimp(subst(sol[2],ansatz)); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text= | |text= | ||
[[Datei:UEBP-31.png|mini|Verläufe von ''w(x), ϕ(x)'']]Die gesuchten Koordinaten ''W'' und ''Φ'' tragen wir über ''α'' auf: | |||
Wir lesen ab: | |||
* für ''α=½'': die Lösung wird - wie erwartet - nur durch ''ϕ<sub>2</sub>'' beschreiben - also ''W'' = 0. | |||
* für ''α= 0'': die Lösung wird - wie erwartet - nur durch ''ϕ<sub>2</sub>'' beschreiben - also W = 0. | |||
Im Plot der normierten Biegelinie des Balkens im Vergleich von Ritz-Näherung zu analytischer Lösung - hier nur für ''a'' = ℓ/2 - zeigt sich, dass die Lösung von deutlich besserer Qualität ist:[[Datei:UEBP-32.png|mini|Vergleich analytische / numerische Lösung für ''w(x)''|alternativtext=|ohne]]Während in [[Gelöste Aufgaben/UEBO|UEBO]] die Näherungslösung gerade mal 1/4 der analytischen Lösung erreichte, haben wir hier fast die gleichen Auslenkungen. Und das, obwohl die Modelle hier und in UEBO jeweils nur zwei Unbekannte haben. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*********************************************************/ | |||
/* post-processing */ | |||
/* plot "weights" W, Φ over a */ | |||
plot2d([subst(sol[2],W)/(M*ℓ^2/(6*EI)),subst(sol[2],Phi)/(M*ℓ/(6*EI))],[alpha,0,1], | |||
[y,-0.5,1.6], | |||
[legend, "W", "Φ"], | |||
[xlabel, "α →"], | |||
[ylabel, "W/(M*ℓ^2/(6*EI)),Φ/(M*ℓ/(6*EI)) →"] ); | |||
/* plot y-axis upside-down */ | |||
preamble: "set yrange [] reverse"; | |||
/* plot displacement w(x) for α = 1/2 */ | |||
toPlot : subst([xi=t, alpha=1/2],[[parametric, alpha *t, ratsimp(subst( ritz,w[1](xi))/W[max]),[t,0,1]], | |||
[parametric, alpha+(1-alpha)*t, ratsimp(subst( ritz,w[2](xi))/W[max]),[t,0,1]], | |||
[parametric, t, ratsimp(subst(analytic,w(xi))/W[max]),[t,0,1]]]); | |||
plot2d(toPlot, | |||
[legend, "section I", "section II", "analytic"], | |||
[color, green, blue, red], | |||
[style, [lines,3], [lines,3], [lines,1]], | |||
[gnuplot_preamble, preamble], | |||
[xlabel, "x/ℓ →"], | |||
[ylabel, "w(x)/W →"] ); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing - Nachtrag | |||
|text=Wir schauen uns auch hier wie in [[Gelöste Aufgaben/UEBO|UEBO]] den Vergleich von Näherungslösung - hier nur für ''α=½'' - und der analytischen Lösung des Biegemomenten-Verlaufs an:[[Datei:UEBP-33.png|mini|Vergleich analytische / numerische Lösung für das Schnittmoment ''M(x)''|alternativtext=|ohne]]Durch das Ansetzen mit zwei separaten Ansatzfunktionen - je eine je Sektion - können wir nun den Sprung im Verlauf der Biegemomente abbilden. Und das macht die Lösung so viel genauer! | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* plot moments My(x) for α = 1/2 */ | ||
toPlot : subst([xi=t, alpha=1/2],[[parametric, alpha *t, EI*diff(ratsimp(subst( ritz,w[1](xi))/M),xi,2)/ell[1]^2,[t,0,1]], | |||
[parametric, alpha+(1-alpha)*t, EI*diff(ratsimp(subst( ritz,w[2](xi))/M),xi,2)/ell[1]^2,[t,0,1]], | |||
[parametric, t, EI*M*ℓ^2/(6*EI)*ratsimp((6*xi-3*(if xi<alpha then 0 else 2))/ℓ^2/M),[t,0,1]]]); | |||
plot2d(toPlot, | |||
[legend, "section I", "section II", "analytic"], | |||
[color, green, blue, red], | |||
[style, [lines,3], [lines,3], [lines,1]], | |||
[gnuplot_preamble, preamble], | |||
[xlabel, "x/ℓ →"], | |||
[ylabel, "M(x)/M →"] ); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
{{MyTip|title=Was noch stört | |||
|text= | |||
Auch wenn die Ergebnisse nun deutlich besser geworden sind - es gibt immer noch Arbeitsschritte, die mühsam sind: | |||
* Die Anpassung der Trial-Functions an die geometrischen Rand- und Übergangsbedingungen. | |||
* Die Integration über die einzelnen Sektionen. | |||
Diese Arbeitsschritte fallen bei der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]] weg, den hier beschriebenen Ansatz entwickelt sie konsequent weiter: | |||
* An der Einleitungsstelle von Kräften und Momenten teilt man die Struktur immer, so dass dort ein Übergang (Knoten) zwischen zwei Sektionen entsteht. Diskrete Kräfte und Momente werden also nur an Knoten eingeleitet. | |||
* Die Trial-Functions werden standardisiert, so dass die geometrischen Übergangsbedingungen zwischen den Sektionen (Elementen) automatisch erfüllt werden → [[Sources/Lexikon/Hermitesche-Polynome|Hermitesche-Polynome]] | |||
* Durch die Verwendung einheitlicher Trial-Functions entfällt die Integration über das Gebiet, wenn man die Element-Steifigkeitsmatrix einmal berechnet hat.}} | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 21. April 2021, 05:02 Uhr
Aufgabenstellung
Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.
Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet.
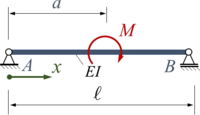
Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.
Im Vergleich zu UEBO, das die gleiche Aufgabenstellung hat - arbeiten wir hier mit Ansatzfunktionen in zwei Sektionen wie bei der FEM. Nur das Gleichgewichts-Prinzip bliebt das Gleicht: das Prinzip vom Minimum der Potentiellen Energie.
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
Statt mit
- Ansatzfunktionen über die gesamte Länge des Balkens arbeiten wir
- hier mit zwei Finiten Elementen (Sektionen), für die wir separat ansetzen.
Header
Wir berechnen die Potentielle Energie U des Systems in Abhängigkeit von den generalisierten Koordinaten Wi und erhalten aus
die Gleichung für den gesuchten Koeffizienten Wi der Trial-Funktionen.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2019-10-19 */
/* ref: TMC, Labor 3 */
/* description: Ritz / FEM approach to EBB, load-case 5*/
/* */
/*******************************************************/
/* declare variables and functions */
declare("Π", alphabetic); /* strain energy */
declare("ℓ", alphabetic);
assume(ℓ>0);
dimless:[x=xi*ℓ,
a=alpha*ℓ];
Declarations
Um die Lösung dimensionslos zu machen, nutzen wir wieder die analytische Lösung des Problems und
- : die maximale Auslenkung des Balkens für a=ℓ.
Dimensionslose Orts-Koordinaten sind
- .
/*********************************************************/
/*analytic solution vgl. Euler-Bernoulli-Blaken/Standard-Lösungen#case5*/
analytic: w(xi) = M*ℓ^2/(6*EI)*(xi^3+xi*(2-6*alpha+3*alpha^2)
/* foeppel-function */
- 3*(if xi<alpha then 0 else xi-alpha)^2);
W[max] : M*ℓ^2/(9*sqrt(3)*EI);
Formfunctions
Dass wir in UEBO die Trial-Funktions ϕ über die gesamte Stablänge angesetzt haben, führt bei den berechneten Näherungen für die Momente M(x) und letztlich auch für die Verschiebungen w(x) zu massiven Fehlern. Einen Sprung in der Momenten-Kennlinie mit einem Polynom zu approximieren, geht halt nicht gut.
Ein Schritt hin zur Methode der Finiten Elemente ist bei diesem "modifizierten Verfahren von Rayleigh-Ritz" der Ansatz der Trial-Functions in zwei Sektionen - also wie bei analytischen Lösung auch.
Die Sektions- (Element-) Längen sind dabei
- für Sektion I: und
- für Sektion II: .
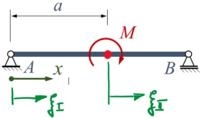
Und wir arbeiten mit je einer Ortskoordinate ξi je Sektion, also
mit
Für die Trial-Functions wählen wir sektionsweise Polynome zweiten Grades
- ,
deren Koeffizienten cij wir nun an die geometrischen Randbedingungen anpassen müssen:
Zusätzlich ersetzen wir zwei cij durch die Verschiebung und Verdrehung im Momenten-Einleitungspunkt
- ,
so dass die Trial-Functions die Form
annehmen bzw.
Im Plot sehen die vier Funktionen (zwei je Sektion, zwei Sektionen) so aus:
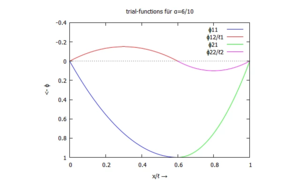
/*********************************************************/
/* declare trial-function(s) */
ell : [alpha*ℓ,(1-alpha)*ℓ];
phi : makelist(sum(c[i,j]*xi^j,j,0,2),i,1,2);
/*********************************************************/
/* boundary-conditions for geometric boundary conditions */
GBC: [subst([xi = 0 ], phi[1] ) = 0,
subst([xi = 1 ], phi[1] ) = subst([xi = 0 ], phi[2] ),
subst([xi = 1 ], phi[1] ) = W,
subst([xi = 1 ], diff(phi[1],xi)/ell[1]) = Phi,
subst([xi = 1 ], diff(phi[1],xi)/ell[1]) = subst([xi = 0 ], diff(phi[2],xi)/ell[2]),
subst([xi = 1 ], phi[2] ) = 0];
sol[1] : solve(GBC,[c[1,0],c[2,0],c[1,1],c[2,1],c[1,2],c[2,2]])[1];
phi: expand(ratsimp(subst(sol[1],phi)));
phi : ratsimp(makelist(makelist(coeff(phi[i],[W,Phi][j]),j,1,2),i,1,2));
/*********************************************************/
toPlot : [[parametric, alpha *t, phi[1][1] , [t,0,1]],
[parametric, alpha *t, phi[1][2]/ℓ, [t,0,1]],
[parametric, alpha+(1-alpha)*t, phi[2][1] , [t,0,1]],
[parametric, alpha+(1-alpha)*t, phi[2][2]/ℓ, [t,0,1]]];
toPlot : subst([xi=t, alpha=6/10], toPlot);
preamble: "set yrange [] reverse";
plot2d(toPlot, [y,-0.4,1],
[legend, "ϕ11 ","ϕ12/ℓ1","ϕ21 ","ϕ22/ℓ2"],
[gnuplot_preamble, preamble],
[title, "trial-functions für α=6/10"],
[xlabel, "x/ℓ →"],
[ylabel, "<- ϕ"] );
ansatz: makelist(w[i](xi) = sum(phi[i][j]*[W,Phi][j],j,1,2),i,1,2);
Potential Energy
Für die Gleichgewichtsbedingungen setzten wir Π (aus Abschnitt Euler-Bernoulli-Balken) und A in U ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir
berücksichtigen und erhalten mit der Arbeitsfunktion des Moments
das Potential in Matrix-Schreibweise:
- .
wobei
- .
/*********************************************************/
/* define potential energy of system */
PMPE : [U = Π - A,
Π = sum(1/2*EI/ell[i]^3*'integrate('diff(w[i](xi),xi,2)^2,xi,0,1),i,1,2),
A = M*Phi];
PMPE: subst(ansatz, subst(PMPE[3],subst(PMPE[2], PMPE[1])));
PMPE : expand(ev(PMPE,nouns));
/* unknowns */
Q : [W,Phi];
Equilibrium Conditions
Diese Gleichung erfüllt die Gleichgewichtsbedingungen
- ,
wenn
- .
Hier kann man schon am Gleichungssystem ablesen, was für α=½ passiert: dann werden die Nebendiagonal-Elemente mit Ihren (2 α-1)-Koeffizienten zu Null, dann ist
- und
- .
/* equilibrium condition */
eom : makelist(expand(diff(subst(PMPE,U),Q[i])),i,1,2);
A : funmake('matrix, makelist(makelist(coeff(eom[i],Q[j]),j,1,2),i,1,2));
b : - funmake('matrix, makelist([subst(makelist(Q[j]=0,j,1,2),eom[i])],i,1,2));
print(A,"∙",transpose(Q),"=",b)$
Solving
Auflösen der Gleichungen nach den unbekannten Koordinaten W und Φ liefert
- .
Damit ist die gesuchte Näherungs-Lösung
- .
/*********************************************************/
/* solve */
sol[2] : ratsimp(solve(eom,Q))[1];
/* approximated solution */
ritz : ratsimp(subst(sol[2],ansatz));
Post-Processing
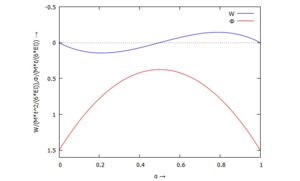
Die gesuchten Koordinaten W und Φ tragen wir über α auf:
Wir lesen ab:
- für α=½: die Lösung wird - wie erwartet - nur durch ϕ2 beschreiben - also W = 0.
- für α= 0: die Lösung wird - wie erwartet - nur durch ϕ2 beschreiben - also W = 0.
Im Plot der normierten Biegelinie des Balkens im Vergleich von Ritz-Näherung zu analytischer Lösung - hier nur für a = ℓ/2 - zeigt sich, dass die Lösung von deutlich besserer Qualität ist:
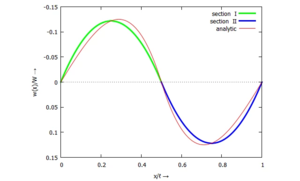
Während in UEBO die Näherungslösung gerade mal 1/4 der analytischen Lösung erreichte, haben wir hier fast die gleichen Auslenkungen. Und das, obwohl die Modelle hier und in UEBO jeweils nur zwei Unbekannte haben.
/*********************************************************/
/* post-processing */
/* plot "weights" W, Φ over a */
plot2d([subst(sol[2],W)/(M*ℓ^2/(6*EI)),subst(sol[2],Phi)/(M*ℓ/(6*EI))],[alpha,0,1],
[y,-0.5,1.6],
[legend, "W", "Φ"],
[xlabel, "α →"],
[ylabel, "W/(M*ℓ^2/(6*EI)),Φ/(M*ℓ/(6*EI)) →"] );
/* plot y-axis upside-down */
preamble: "set yrange [] reverse";
/* plot displacement w(x) for α = 1/2 */
toPlot : subst([xi=t, alpha=1/2],[[parametric, alpha *t, ratsimp(subst( ritz,w[1](xi))/W[max]),[t,0,1]],
[parametric, alpha+(1-alpha)*t, ratsimp(subst( ritz,w[2](xi))/W[max]),[t,0,1]],
[parametric, t, ratsimp(subst(analytic,w(xi))/W[max]),[t,0,1]]]);
plot2d(toPlot,
[legend, "section I", "section II", "analytic"],
[color, green, blue, red],
[style, [lines,3], [lines,3], [lines,1]],
[gnuplot_preamble, preamble],
[xlabel, "x/ℓ →"],
[ylabel, "w(x)/W →"] );
Post-Processing - Nachtrag
Wir schauen uns auch hier wie in UEBO den Vergleich von Näherungslösung - hier nur für α=½ - und der analytischen Lösung des Biegemomenten-Verlaufs an:
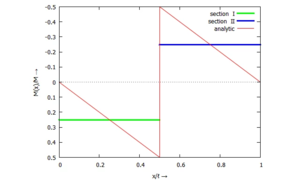
Durch das Ansetzen mit zwei separaten Ansatzfunktionen - je eine je Sektion - können wir nun den Sprung im Verlauf der Biegemomente abbilden. Und das macht die Lösung so viel genauer!
/* plot moments My(x) for α = 1/2 */
toPlot : subst([xi=t, alpha=1/2],[[parametric, alpha *t, EI*diff(ratsimp(subst( ritz,w[1](xi))/M),xi,2)/ell[1]^2,[t,0,1]],
[parametric, alpha+(1-alpha)*t, EI*diff(ratsimp(subst( ritz,w[2](xi))/M),xi,2)/ell[1]^2,[t,0,1]],
[parametric, t, EI*M*ℓ^2/(6*EI)*ratsimp((6*xi-3*(if xi<alpha then 0 else 2))/ℓ^2/M),[t,0,1]]]);
plot2d(toPlot,
[legend, "section I", "section II", "analytic"],
[color, green, blue, red],
[style, [lines,3], [lines,3], [lines,1]],
[gnuplot_preamble, preamble],
[xlabel, "x/ℓ →"],
[ylabel, "M(x)/M →"] );
| ✔ Was noch stört: |
Auch wenn die Ergebnisse nun deutlich besser geworden sind - es gibt immer noch Arbeitsschritte, die mühsam sind:
Diese Arbeitsschritte fallen bei der Finite Elemente Methode weg, den hier beschriebenen Ansatz entwickelt sie konsequent weiter:
|
Links
- ...
Literature
- ...