Gelöste Aufgaben/UEBO: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
Der Euler-Bernoulli-Balken ''AB'' wird durch ein Moment ''M'' zwischen den beiden gelenkigen Lagern belastet. | Der Euler-Bernoulli-Balken ''AB'' wird durch ein Moment ''M'' zwischen den beiden gelenkigen Lagern belastet. | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:EBB-load-case-05.png|alternativtext=|links|200px|Lageplan]] | [[Datei:EBB-load-case-05.png|alternativtext=|mini|links|200px|Lageplan]] | ||
Gesucht ist eine Lösung für die Biegelinie mit dem [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Verfahren von Rayleigh-Ritz (EBB)|Ansatz von Ritz]] und zwei Trial-Funktionen. | Gesucht ist eine Lösung für die Biegelinie mit dem [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Verfahren von Rayleigh-Ritz (EBB)|Ansatz von Ritz]] und zwei Trial-Funktionen. | ||
(Weg "1" wie in [[Gelöste Aufgaben/UEBH|UEBH]] beschrieben.)</onlyinclude> | (Weg "1" wie in [[Gelöste Aufgaben/UEBH|UEBH]] beschrieben.) | ||
</onlyinclude> | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
| Zeile 26: | Zeile 26: | ||
* [[Sources/Lexikon/Ansatzfunktion|Ansatzfunktionen]] über die gesamte Länge des Balkens. | * [[Sources/Lexikon/Ansatzfunktion|Ansatzfunktionen]] über die gesamte Länge des Balkens. | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text= | ||
Wir berechnen die Potentielle Energie '''''U''''' des Systems in Abhängigkeit von den generalisierten Koordinaten ''W<sub>i</sub>'' und erhalten aus | |||
::<math>\displaystyle \frac{d\,U}{d\,W_i} \stackrel{!}{=} 0 </math> | |||
die Gleichung für den gesuchten Koeffizienten ''W<sub>i</sub>'' der Trial-Funktionen. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2019-10-13 */ | |||
/* ref: TMC, Labor 4 */ | |||
/* description: Ritz approach to EBB, load-case 5 */ | |||
/* */ | |||
/*******************************************************/ | |||
/* declare variables and functions */ | |||
declare("Π", alphabetic); /* strain energy */ | |||
assume(ℓ>0); | |||
dimless:[x=xi*ℓ, | |||
a=alpha*ℓ]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text= | |text= | ||
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des Problems , hier die Beträge der maximalen Auslenkung des Balkens für ''a = ℓ'' und der Verdrehung des Balkens am Momenten-Angriffspunkt für ''a = ℓ/2'': | |||
<table class="wikitable" style="background-color:white; margin-right:14px; | |||
"> | |||
<tr><td><math>W^{max} = \displaystyle \frac{M\,\ell^2}{9\sqrt{3}\,\cdot E\,I}</math></td><td>die maximale Auslenkung des Balkens für a=''ℓ'' | |||
</td></tr> | |||
<tr><td><math>\Phi^M= \displaystyle \frac{M\,\ell}{12\cdot E\,I}</math></td><td>die Verdrehung des Balkens am Momenten-Angriffspunkt für a=''ℓ''/2</td></tr> | |||
</table> | |||
Dimensionslose Orts-Koordinaten sind | |||
::<math>\begin{array}{ll} x &= \xi\cdot \ell,\\ a &= \alpha\cdot \ell. \end{array}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /*analytic solution vgl. Lexikon/Euler-Bernoulli-Blaken */ | ||
analytic: w(xi) = M*ℓ^2/(6*EI)*(xi^3+xi*(2-6*alpha+3*alpha^2) | |||
/* foeppel-function */ | |||
- 3*(if xi<alpha then 0 else xi-alpha)^2); | |||
sectionI : M*ℓ^2/(6*EI)*(xi^3+xi*(2-6*alpha+3*alpha^2)); | |||
/* make dim'less with load case #5 */ | |||
Phi[C] : subst([xi=1/2],diff(subst([alpha=1/2],sectionI),xi)/ℓ); | |||
W[max] : -subst([alpha=1],subst(solve( | |||
diff(subst([alpha=1],sectionI),xi)/ℓ=0,xi)[2],sectionI)); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text= | |text= | ||
Bei der Suche nach passenden Trial-Functions ''ϕ'' lassen wir uns ebenfalls von der analytischen Lösung des Problems "inspirieren": | |||
::<math>w_a = \displaystyle \frac{M \ell^2}{3 EI} \left( \left(3\cdot {{\alpha}^{2}}-6\cdot \alpha+2\right) \cdot \xi+{{\xi}^{3}}-3<\xi-\alpha>^2\right)</math> | |||
Der Funktionsverlauf von ''w<sup>a</sup>'' hat zwei charakteristische Ausprägungen:<table class="wikitable" style="background-color:white; margin-right:14px; | |||
"> | |||
<tr><th>... für a=0</th><th>... für a=ℓ/2</th></tr> | |||
<tr><td>[[Datei:EBB-load-case-06-alpha00.png|alternativtext=|rahmenlos]] | |||
</td><td>[[Datei:EBB-load-case-06-alpha05.png|rahmenlos]] | |||
</td></tr> | |||
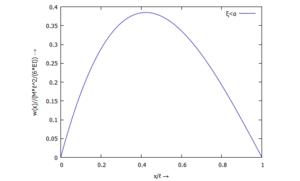
<tr><td>Diese Lösung - mit dem angreifenden Moment in A - hat eine starke symmetrische Komponente bzgl der Stab-Mitte. | |||
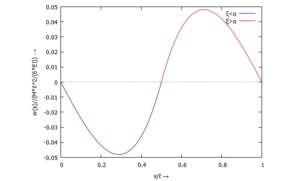
</td><td>Diese Lösung - mit dem angreifenden Moment in der Stab-Mitte - ist punktsymmetrisch zum Momenten-Angriffspunkt. | |||
</td></tr> | |||
</table> | |||
Und so wählen wir unsere Trial-Functions als | |||
::<math>\phi_1 = c_1 \cdot \xi \cdot (1-\xi) \text{ und } | |||
\phi_2 = c_2 \cdot \xi \cdot (1-\xi) \cdot (\alpha-\xi)</math>. | |||
[[Datei:UEBO-11.png|mini|Trial-Functions]]Für α=7∙ℓ/10 sehen sie so aus; | |||
Die Koeffizienten ''c<sub>1</sub>'' und ''c<sub>2</sub>'' haben wir dabei so gewählt, dass | |||
::<math>\begin{array}{ll} | |||
\phi_1(\displaystyle\frac{1}{2})&=1\\ | |||
\phi_2'(\alpha)&=1 | |||
\end{array}</math>. | |||
Mit den neuen, gesuchten Wichtungsfaktoren ''q<sub>w</sub>'' und ''q<sub>ϕ</sub>'' ist die Ansatzfunktion zur Lösung mit dem [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Verfahren von Rayleigh-Ritz (EBB)|Verfahren von Rayleigh-Ritz]] damit | |||
<math>\displaystyle w(\xi) = \frac{M \ell^2}{3 EI} \left( | |||
q_w \left( 4 \frac{\xi-\xi^2}{3 \sqrt{3}}\right) + | |||
q_\phi \left(-\xi^3+(1+\alpha) \xi^2-\alpha \xi \right) | |||
\right)</math> | |||
Aufgrund der gewählten Skalierungsfaktoren erwarten wir als Ergebnis näherungsweise | |||
* für ''α=½'': ''q<sub>w</sub>'' ≈ 0 und ''q<sub>ϕ</sub>'' ≈ 1, | |||
* für ''α= 0'': ''q<sub>w</sub>'' ≈ 1 und ''q<sub>ϕ</sub>'' ≈ 0. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* derive trial-function(s) */ | ||
phi : [c[1]*xi*(1-xi), c[2]*xi*(1-xi)*(alpha-xi)]; | |||
GBC: [subst([xi = 1/2 ], phi[1] )= 1, | |||
subst([xi = 1/2 ], diff(phi[2],xi)/ℓ)= 1]; | |||
sol[1] : solve(GBC,[c[1],c[2]])[1]; | |||
phi: ratsimp(subst(sol[1],phi)); | |||
ansatz: [w(xi) = q[w]*W[max]*phi[1] + q[p]*Phi[C]*phi[2]]; | |||
preamble: "set yrange [] reverse"; | |||
plot2d(subst([alpha=7/10],[phi[1],phi[2]/ℓ]),[xi,0,1], | |||
[legend, "ϕ1","ϕ2/ℓ"], | |||
[gnuplot_preamble, preamble], | |||
[title, "trial-functions für α=7/10"], | |||
[xlabel, "ξ →"], | |||
[ylabel, "<- ϕ"] ); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Potential Energy | {{MyCodeBlock|title=Potential Energy | ||
|text= | |text= | ||
Für die Gleichgewichtsbedingungen setzten wir ''Π'' (aus Abschnitt [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]]) und ''A'' in ''U'' ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir | |||
::<math>\displaystyle \frac{d\phi}{x} = \frac{d\phi}{\xi}\cdot\underbrace{\displaystyle\frac{d\xi}{x}}_{\displaystyle = \frac{1}{\ell}}</math> | |||
berücksichtigen und erhalten mit der Arbeitsfunktion des Moments | |||
::<math>A = M \cdot w'|_{\displaystyle \xi=\alpha}</math> | |||
das Potential in Matrix-Schreibweise: | |||
::<math>U = \displaystyle \frac{1}{2} \cdot \displaystyle \underline{Q}^T \cdot \underline{\underline{A}}\cdot \underline{Q} - \underline{Q}^T\cdot \underline{b} </math>. | |||
wobei | |||
::<math>\underline{Q} = \left(\begin{array}{c}q_w\\q_\phi\end{array}\right)</math>. | |||
Einsetzen der Ansatzfunktion in die [[Sources/Lexikon/Formänderungsenergie|Formänderungsenergie]] und die [[Sources/Lexikon/Arbeitsfunktion|Arbeitsfunktion]] liefert für die Matrizen ''A'' und ''b'': | |||
::<math>\underline{\underline{A}} = \begin{pmatrix}\displaystyle \frac{128}{81} & \displaystyle \frac{16}{{{3}^{\frac{5}{2}}}}-\frac{32\cdot \alpha}{{{3}^{\frac{5}{2}}}}\\ \displaystyle \frac{16}{{{3}^{\frac{5}{2}}}}-\frac{32\cdot \alpha}{{{3}^{\frac{5}{2}}}} & \displaystyle \frac{8\cdot {{\alpha}^{2}}}{3}-\frac{8\cdot \alpha}{3}+\frac{8}{3}\end{pmatrix}</math>, | |||
::<math>\underline{b} = \begin{pmatrix}\displaystyle \frac{8}{{{3}^{\frac{3}{2}}}}-\frac{16\cdot \alpha}{{{3}^{\frac{3}{2}}}}\\ \displaystyle 2\cdot \alpha-2\cdot {{\alpha}^{2}}\end{pmatrix}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | |||
/* define potential energy of system */ | |||
PMPE : [U = Π - A, | |||
Π = 1/2*EI/ℓ^3*'integrate('diff(w(xi),xi,2)^2,xi,0,1), | |||
A = M*Phi(a)]; | |||
PMPE: subst([Phi(a) = subst([xi=alpha],diff(subst(ansatz,w(xi))/ℓ,xi))], | |||
subst(ansatz, | |||
subst(PMPE[3],subst(PMPE[2], PMPE[1])))); | |||
PMPE : expand(ev(PMPE,nouns)); | |||
/* unknowns */ | |||
Q : [q[w],q[p]]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text= | |text= | ||
Diese Gleichung erfüllt die Gleichgewichtsbedingungen | |||
::<math>\displaystyle \frac{dU}{dQ_i} \stackrel{!}{=} 0</math>, | |||
wenn | |||
::<math>\begin{pmatrix}\displaystyle \frac{128}{81} &\displaystyle \frac{16}{{{3}^{\frac{5}{2}}}}-\frac{32\cdot \alpha}{{{3}^{\frac{5}{2}}}}\\\displaystyle \frac{16}{{{3}^{\frac{5}{2}}}}-\frac{32\cdot \alpha}{{{3}^{\frac{5}{2}}}} &\displaystyle \frac{8\cdot {{\alpha}^{2}}}{3}-\frac{8\cdot \alpha}{3}+\frac{8}{3}\end{pmatrix} | |||
\cdot | |||
\begin{pmatrix}{{q}_{w}}\\ {{q}_{p}}\end{pmatrix}=\begin{pmatrix}\displaystyle \frac{8}{{{3}^{\frac{3}{2}}}}-\frac{16\cdot \alpha}{{{3}^{\frac{3}{2}}}}\\\displaystyle 2\cdot \alpha-2\cdot {{\alpha}^{2}}\end{pmatrix}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* equilibrium condition */ | ||
eom : makelist(expand(diff(subst(PMPE,U)/(M^2*ℓ/(6*EI)),Q[i])),i,1,2); | |||
A : funmake('matrix, makelist(makelist(coeff(eom[i],Q[j]),j,1,2),i,1,2)); | |||
b : - funmake('matrix, makelist([subst(makelist(Q[j]=0,j,1,2),eom[i])],i,1,2)); | |||
print(A,"∙",transpose(Q),"=",b)$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text= | |text= | ||
Auflösen der Gleichungen nach den unbekannten Koordinaten ''q<sub>w</sub>'' und ''q<sub>ϕ</sub>'' liefert | |||
::<math>\begin{array}{ll} | |||
q_w & =-\frac{3^{\frac{3}{2}}}{8} \left(-2+7 \alpha-9 \alpha^2+6 \alpha^3\right)\\ | |||
q_\phi &=-\frac{1}{2} \left(1-6 \alpha+6 \alpha^2\right) | |||
\end{array}</math>. | |||
Damit ist die gesuchte Näherungs-Lösung | |||
::<math>\displaystyle w( \xi) =\frac{M\,\ell^2}{6\,EI} \left( \left( 3\cdot {{\alpha}^{2}}-6\cdot \alpha+2\right) \cdot \xi+\left( -9\cdot {{\alpha}^{2}}+12\cdot \alpha-3\right) \cdot {{\xi}^{2}}+\left( 6\cdot {{\alpha}^{2}}-6\cdot \alpha+1\right) \cdot {{\xi}^{3}}\right)</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* solve */ | ||
sol[2] : ratsimp(solve(equcon,[W,Phi]))[1]; | |||
/* ... or in dimensionless coordinates */ | |||
sol[3] : ratsimp(solve(subst(dimless[1],equcon),[q[w],q[phi]]))[1]; | |||
/* approximated solution */ | |||
ritz : w(xi)=ratsimp(subst(sol[2],subst(dimless[2],rhs(trial)))); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text= | |text= | ||
[[Datei:UEBO-31.png|mini|Verlauf der Koordinaten ''q<sub>w</sub>, q<sub>ϕ</sub>'']]Die gesuchten Koordinaten ''q<sub>w</sub>'' und ''q<sub>Φ</sub>'' sind dimensionslos. Wir können sie direkt für verschiedene Werte von ''α'' auftragen. | |||
Wir sehen: | |||
* für ''α=½'': die Lösung wird - wie erwartet - nur durch ''ϕ<sub>2</sub>'' beschreiben - also ''q<sub>w</sub>'' ≈ 0 und ''q<sub>ϕ</sub>'' ≈ 1; allerdings ist die Qualität der Lösung mit ''q<sub>ϕ</sub>'' = 1/4 sehr schlecht - hier drückt der Sprung in der Momenten-Kennlinie der analytischen Lösung auf das Ergebnis (s.u.). | |||
* für ''α= 0'': die Lösung wird - wie erwartet - primär durch ''ϕ<sub>1</sub>'' beschreiben, also ''q<sub>w</sub>'' ≈ 1 und ''q<sub>ϕ</sub>'' ≈ 0. Hier zeigt die Lösung mit ''q<sub>w</sub>'' = 1.3 und ''q<sub>ϕ</sub>'' = -0.5 einen recht großen Lösungs-Anteil der punktsymmetrischen Trial-Function. | |||
[[Datei:UEBO-32.png|mini|Parameterstudie Biegelinie]] | |||
Und so sieht die normierte Biegelinie des Balkens im Vergleich von Ritz-Näherung zu analytischer Lösung für verschiedene Werte von ''a'' aus: | |||
Die dicken Linien gehören zu Näherung nach dem Ritz-Ansatz, die dünnen zur analytischen Lösung. Je weiter der Momenten-Angriffspunkt in die Balken-Mitte rückt und besonders für ''α=1/2'' liefert der Ritz-Ansatz kein überzeugendes Ergebnis. Hier müssten wir mehr Trial-Functions "spendieren". | |||
[[Datei:UEBO-33.png|mini|Vergleich: analytische / numerische Lösung für den Biegemomenten-Verlauf.]] | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* post-processing */ | ||
/* plot solutions */ | |||
preamble: "set yrange [] reverse"; | |||
plot2d([subst(sol[2],q[w]),subst(sol[2],q[p])],[alpha,0,1], | |||
[legend, "q[w]", "q[Φ]"], | |||
[gnuplot_preamble, preamble], | |||
[xlabel, "α →"], | |||
[ylabel, "q[w],q[Φ] →"] ); | |||
/* plot w(x) for different αs */ | |||
/* and compare analytic with Ritz-solution */ | |||
leg : append([legend], makelist(simplode (["α = ",i,"/10"]),i,1,9,2)); | |||
toPlot : [makelist(subst([alpha=i/10],ratsimp(subst(ritz,w(xi))/W[max])), i,1,9,2), | |||
makelist(subst([alpha=i/10],ratsimp(subst(analytic,w(xi))/W[max])), i,1,9,2)]; | |||
plot2d(append(toPlot[1],toPlot[2]),[xi,0,1], | |||
leg, | |||
[color, green, blue, red, magenta, black], | |||
[style, [lines,3], [lines,3], [lines,3], [lines,3], [lines,3], [lines,1], [lines,1], [lines,1], [lines,1], [lines,1]], | |||
[gnuplot_preamble, preamble], | |||
[xlabel, "x/ℓ →"], | |||
[ylabel, "w(x)/W →"] ); | |||
</syntaxhighlight> | |||
}} | |||
{{MyCodeBlock|title=Post-Processing - Nachtrag | |||
|text= | |||
Wieso die Näherungslösung - besonders für ''α=½'' - so schlecht ist, erkennt man beim Auftragen der Biegemomente im Stab für | |||
* die analytische Lösung | |||
::<math>\displaystyle \frac{M(x)}{M} = \left\{ | |||
\begin{array}{cl} | |||
-\xi&\ldots\text{ für } \xi<\frac{1}{2}\\ | |||
1-\xi&\ldots\text{ sonst. } | |||
\end{array} | |||
\right.</math> und | |||
* die numerische Lösung | |||
::<math>\displaystyle \frac{M(x)}{M} = \frac{1}{4} (2 \xi-1)</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1>/* Vergleich der Momenten-Kennlinien */ | |||
displacements : M*ℓ^2/(6*EI)*[[(xi^3+xi*(2-6*alpha+3*alpha^2)), (xi^3+xi*(2-6*alpha+3*alpha^2) - 3*(xi-alpha)^2)], | |||
[((3*alpha^2-6*alpha+2)*xi+(-9*alpha^2+12*alpha-3)*xi^2+(6*alpha^2-6*alpha+1)*xi^3)]]; | |||
bendingmoments: subst([xi=t],subst([alpha=1/2],-EI*diff(displacements,xi,2)/ℓ^2/M)); | |||
plot2d([[parametric, t, bendingmoments[1][1], [t, 0, 1/2]], | |||
[parametric, t, bendingmoments[1][2], [t, 1/2, 1]], | |||
[parametric, t, bendingmoments[2][1], [t, 0 , 1]]], | |||
[color, red, red, blue], | |||
[style, [lines,1], [lines,1], [lines,3]], | |||
[legend, "analytic, section I", "analytic, section II", "Rayleigh-Ritz"], | |||
[xlabel, "x/ℓ →"], | |||
[ylabel, "M(x)/M →"] ); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr /> | ||
'''Links''' | '''Links''' | ||
* ... | * ... | ||
| Zeile 110: | Zeile 320: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 21. April 2021, 05:01 Uhr
Aufgabenstellung
Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.
Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet.
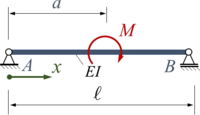
Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.
(Weg "1" wie in UEBH beschrieben.)
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
- dem Prinzip vom Minimum der Potentiellen Energie und
- Ansatzfunktionen über die gesamte Länge des Balkens.
Header
Wir berechnen die Potentielle Energie U des Systems in Abhängigkeit von den generalisierten Koordinaten Wi und erhalten aus
die Gleichung für den gesuchten Koeffizienten Wi der Trial-Funktionen.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2019-10-13 */
/* ref: TMC, Labor 4 */
/* description: Ritz approach to EBB, load-case 5 */
/* */
/*******************************************************/
/* declare variables and functions */
declare("Π", alphabetic); /* strain energy */
assume(ℓ>0);
dimless:[x=xi*ℓ,
a=alpha*ℓ];
Declarations
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des Problems , hier die Beträge der maximalen Auslenkung des Balkens für a = ℓ und der Verdrehung des Balkens am Momenten-Angriffspunkt für a = ℓ/2:
| die maximale Auslenkung des Balkens für a=ℓ | |
| die Verdrehung des Balkens am Momenten-Angriffspunkt für a=ℓ/2 |
Dimensionslose Orts-Koordinaten sind
- .
/*analytic solution vgl. Lexikon/Euler-Bernoulli-Blaken */
analytic: w(xi) = M*ℓ^2/(6*EI)*(xi^3+xi*(2-6*alpha+3*alpha^2)
/* foeppel-function */
- 3*(if xi<alpha then 0 else xi-alpha)^2);
sectionI : M*ℓ^2/(6*EI)*(xi^3+xi*(2-6*alpha+3*alpha^2));
/* make dim'less with load case #5 */
Phi[C] : subst([xi=1/2],diff(subst([alpha=1/2],sectionI),xi)/ℓ);
W[max] : -subst([alpha=1],subst(solve(
diff(subst([alpha=1],sectionI),xi)/ℓ=0,xi)[2],sectionI));
Formfunctions
Bei der Suche nach passenden Trial-Functions ϕ lassen wir uns ebenfalls von der analytischen Lösung des Problems "inspirieren":
Der Funktionsverlauf von wa hat zwei charakteristische Ausprägungen:
Und so wählen wir unsere Trial-Functions als
- .
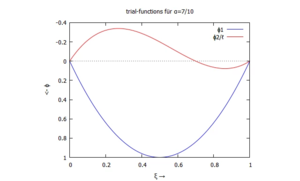
Für α=7∙ℓ/10 sehen sie so aus;
Die Koeffizienten c1 und c2 haben wir dabei so gewählt, dass
- .
Mit den neuen, gesuchten Wichtungsfaktoren qw und qϕ ist die Ansatzfunktion zur Lösung mit dem Verfahren von Rayleigh-Ritz damit
Aufgrund der gewählten Skalierungsfaktoren erwarten wir als Ergebnis näherungsweise
- für α=½: qw ≈ 0 und qϕ ≈ 1,
- für α= 0: qw ≈ 1 und qϕ ≈ 0.
/* derive trial-function(s) */
phi : [c[1]*xi*(1-xi), c[2]*xi*(1-xi)*(alpha-xi)];
GBC: [subst([xi = 1/2 ], phi[1] )= 1,
subst([xi = 1/2 ], diff(phi[2],xi)/ℓ)= 1];
sol[1] : solve(GBC,[c[1],c[2]])[1];
phi: ratsimp(subst(sol[1],phi));
ansatz: [w(xi) = q[w]*W[max]*phi[1] + q[p]*Phi[C]*phi[2]];
preamble: "set yrange [] reverse";
plot2d(subst([alpha=7/10],[phi[1],phi[2]/ℓ]),[xi,0,1],
[legend, "ϕ1","ϕ2/ℓ"],
[gnuplot_preamble, preamble],
[title, "trial-functions für α=7/10"],
[xlabel, "ξ →"],
[ylabel, "<- ϕ"] );
Potential Energy
Für die Gleichgewichtsbedingungen setzten wir Π (aus Abschnitt Euler-Bernoulli-Balken) und A in U ein und schreiben die skalare Gleichung allgemein in Matrizenform an. Dabei müssen wir
berücksichtigen und erhalten mit der Arbeitsfunktion des Moments
das Potential in Matrix-Schreibweise:
- .
wobei
- .
Einsetzen der Ansatzfunktion in die Formänderungsenergie und die Arbeitsfunktion liefert für die Matrizen A und b:
- ,
- .
/* define potential energy of system */
PMPE : [U = Π - A,
Π = 1/2*EI/ℓ^3*'integrate('diff(w(xi),xi,2)^2,xi,0,1),
A = M*Phi(a)];
PMPE: subst([Phi(a) = subst([xi=alpha],diff(subst(ansatz,w(xi))/ℓ,xi))],
subst(ansatz,
subst(PMPE[3],subst(PMPE[2], PMPE[1]))));
PMPE : expand(ev(PMPE,nouns));
/* unknowns */
Q : [q[w],q[p]];
Equilibrium Conditions
Diese Gleichung erfüllt die Gleichgewichtsbedingungen
- ,
wenn
- .
/* equilibrium condition */
eom : makelist(expand(diff(subst(PMPE,U)/(M^2*ℓ/(6*EI)),Q[i])),i,1,2);
A : funmake('matrix, makelist(makelist(coeff(eom[i],Q[j]),j,1,2),i,1,2));
b : - funmake('matrix, makelist([subst(makelist(Q[j]=0,j,1,2),eom[i])],i,1,2));
print(A,"∙",transpose(Q),"=",b)$
Solving
Auflösen der Gleichungen nach den unbekannten Koordinaten qw und qϕ liefert
- .
Damit ist die gesuchte Näherungs-Lösung
- .
/* solve */
sol[2] : ratsimp(solve(equcon,[W,Phi]))[1];
/* ... or in dimensionless coordinates */
sol[3] : ratsimp(solve(subst(dimless[1],equcon),[q[w],q[phi]]))[1];
/* approximated solution */
ritz : w(xi)=ratsimp(subst(sol[2],subst(dimless[2],rhs(trial))));
Post-Processing
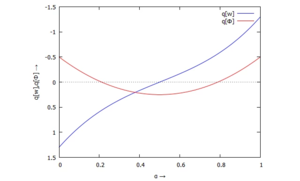
Die gesuchten Koordinaten qw und qΦ sind dimensionslos. Wir können sie direkt für verschiedene Werte von α auftragen.
Wir sehen:
- für α=½: die Lösung wird - wie erwartet - nur durch ϕ2 beschreiben - also qw ≈ 0 und qϕ ≈ 1; allerdings ist die Qualität der Lösung mit qϕ = 1/4 sehr schlecht - hier drückt der Sprung in der Momenten-Kennlinie der analytischen Lösung auf das Ergebnis (s.u.).
- für α= 0: die Lösung wird - wie erwartet - primär durch ϕ1 beschreiben, also qw ≈ 1 und qϕ ≈ 0. Hier zeigt die Lösung mit qw = 1.3 und qϕ = -0.5 einen recht großen Lösungs-Anteil der punktsymmetrischen Trial-Function.
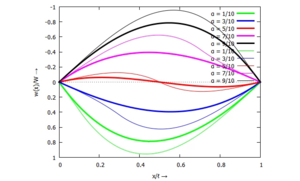
Und so sieht die normierte Biegelinie des Balkens im Vergleich von Ritz-Näherung zu analytischer Lösung für verschiedene Werte von a aus:
Die dicken Linien gehören zu Näherung nach dem Ritz-Ansatz, die dünnen zur analytischen Lösung. Je weiter der Momenten-Angriffspunkt in die Balken-Mitte rückt und besonders für α=1/2 liefert der Ritz-Ansatz kein überzeugendes Ergebnis. Hier müssten wir mehr Trial-Functions "spendieren".
/* post-processing */
/* plot solutions */
preamble: "set yrange [] reverse";
plot2d([subst(sol[2],q[w]),subst(sol[2],q[p])],[alpha,0,1],
[legend, "q[w]", "q[Φ]"],
[gnuplot_preamble, preamble],
[xlabel, "α →"],
[ylabel, "q[w],q[Φ] →"] );
/* plot w(x) for different αs */
/* and compare analytic with Ritz-solution */
leg : append([legend], makelist(simplode (["α = ",i,"/10"]),i,1,9,2));
toPlot : [makelist(subst([alpha=i/10],ratsimp(subst(ritz,w(xi))/W[max])), i,1,9,2),
makelist(subst([alpha=i/10],ratsimp(subst(analytic,w(xi))/W[max])), i,1,9,2)];
plot2d(append(toPlot[1],toPlot[2]),[xi,0,1],
leg,
[color, green, blue, red, magenta, black],
[style, [lines,3], [lines,3], [lines,3], [lines,3], [lines,3], [lines,1], [lines,1], [lines,1], [lines,1], [lines,1]],
[gnuplot_preamble, preamble],
[xlabel, "x/ℓ →"],
[ylabel, "w(x)/W →"] );
Post-Processing - Nachtrag
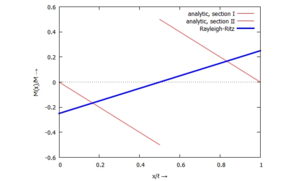
Wieso die Näherungslösung - besonders für α=½ - so schlecht ist, erkennt man beim Auftragen der Biegemomente im Stab für
- die analytische Lösung
- und
- die numerische Lösung
- .
/* Vergleich der Momenten-Kennlinien */
displacements : M*ℓ^2/(6*EI)*[[(xi^3+xi*(2-6*alpha+3*alpha^2)), (xi^3+xi*(2-6*alpha+3*alpha^2) - 3*(xi-alpha)^2)],
[((3*alpha^2-6*alpha+2)*xi+(-9*alpha^2+12*alpha-3)*xi^2+(6*alpha^2-6*alpha+1)*xi^3)]];
bendingmoments: subst([xi=t],subst([alpha=1/2],-EI*diff(displacements,xi,2)/ℓ^2/M));
plot2d([[parametric, t, bendingmoments[1][1], [t, 0, 1/2]],
[parametric, t, bendingmoments[1][2], [t, 1/2, 1]],
[parametric, t, bendingmoments[2][1], [t, 0 , 1]]],
[color, red, red, blue],
[style, [lines,1], [lines,1], [lines,3]],
[legend, "analytic, section I", "analytic, section II", "Rayleigh-Ritz"],
[xlabel, "x/ℓ →"],
[ylabel, "M(x)/M →"] );
Links
- ...
Literature
- ...