Gelöste Aufgaben/TkPb: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „h“ |
Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:A*x=b]] | |||
[[Category:Lineare Algebra]] | |||
[[Category:Analytische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Stab]] | |||
[[Category:Knotenpunktverfahren]] | |||
[[Category:Maxima]] | |||
[[Category:Stabwerk]] | |||
==Aufgabenstellung== | |||
Ein Stabwerk aus 5 Stäben wird durch eine Kraft ''F'' belastet. Alle Stäbe haben die Länge ''a''. | |||
Hier soll eine einfache Stabwerksaufgabe gelöste werden - aber im Hintergrund geht es eigentlich darum, wie dieser Lösungsprozess in einer Software - hier Maxima - umgesetzt wird. | |||
<onlyinclude> | |||
[[Datei:TkPb-01.png|200px|left|mini|Lageplan]] | |||
Gesucht sind die Stab- und Lagerreaktionskräfte des Systems nach dem Knotenpunktverfahren. | |||
</onlyinclude> | |||
== Lösung "per Hand" und mit Maxima == | |||
Beide Lösungsansätz verfolgen wir parallel - bis wir zur Lösung des Gleichungssystems kommen. | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text= | |||
Hier steht nur die Maxima-Headerdatei. Sie soll später helfen, die richtige Versionsnummer der Software zu finden und Ansprechpartner für Nachfragen zu identifizieren. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2016-09-18 */ | |||
/* ref: Ma-2, Unterricht zu Linearer Algebra */ | |||
/* description: solves the linear system of equs */ | |||
/* for the od forces */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
[[Datei:Schema-1-2-.png|rahmenlos]] | |||
[[Datei:TkPb-11.png|mini|Knoten und Stäbe nummerieren.]]Wir nummerieren zunächst die Knoten und Stäbe, damit wir sie im weiteren Lösungsverlauf eindeutig ansprechen können. | |||
Und ein bischen Geometrie Geometrie müssen wir auch ansetzen, um die sin- und cos-Beziehungen von ''α'' zu bekommen: | |||
[[Datei:TkPb-12.png|mini|Geometrie-Zusammenhänge.|alternativtext=|links|287x287px]] | |||
Wir setzen also | |||
::<math>\displaystyle \cos(\alpha) = \frac{1}{2}, \; \sin(\alpha) = \frac{1}{2}\sqrt{3}</math>. | |||
<br clear="all"/> | |||
[[Datei:Schema-2-2-.png|rahmenlos]] | |||
<table class="wikitable" style="background-color:white;"> | |||
<tr><td>Knoten I<br/>[[Datei:TkPb-Knoten-01.png|rahmenlos|alternativtext=|100x100px]]</td> | |||
<td>Knoten II<br/>[[Datei:TkPb-Knoten-02.png|rahmenlos|alternativtext=|130x130px]]</td></tr> | |||
<tr><td>Knoten III<br/>[[Datei:TkPb-Knoten-03.png|rahmenlos|alternativtext=|130x130px]]</td> | |||
<td>Knoten IV<br/>[[Datei:TkPb-Knoten-04.png|rahmenlos|alternativtext=|130x130px]]</td> | |||
</tr></table> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* ---------------------------------------------------- */ | |||
/* geometry */ | |||
geom : [cos(alpha) = 1/2, sin(alpha) = 1/2*sqrt(3)]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
[[Datei:Schema-3-2-.png|rahmenlos]] | |||
[[Datei:TkPb-13.png|mini|Die Gleichgewichtsbedingungen ...|alternativtext=|500x500px]]Wir schreiben je Knoten die zwei Gleichgewichtsbedingungen an, die Koeffizienten schreiben wir dabei schon mal so an, wie sie hinterher in der System-Matrix auftauchen sollen: | |||
[[Datei:TkPb-14.png|mini|... formuliert in Maxima.|alternativtext=|links|400x400px]] | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* ---------------------------------------------------- */ | |||
/* equilibrium conditions at nodes */ | |||
equs : [+ A[y] + S[1]*sin(alpha) = 0, | |||
+ S[1]*cos(alpha) + S[2] = 0, | |||
- S[1]*sin(alpha) - S[3]*sin(alpha) - F = 0, | |||
- S[1]*cos(alpha) + S[3]*cos(alpha) + S[4] = 0, | |||
+ S[3]*sin(alpha) + S[5]*sin(alpha) = 0, | |||
- S[2] - S[3]*cos(alpha) + S[5]*cos(alpha) = 0, | |||
- S[5]*sin(alpha) + B[y] = 0, | |||
- S[4] - S[5]*cos(alpha) + B[x] = 0]; | |||
/* unknowns */ | |||
x : [ A[y], S[1], S[2], S[3], S[4], S[5], B[y], B[x]]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Check for Solvability | |||
|text= | |||
[[Datei:Schema-4-2-.png|rahmenlos]] | |||
[[Datei:TkPb-15.png|mini|Haben wir genug Gleichungen für alle Unbekannten?|alternativtext=|300px|left]]Ja - so sieht es aus. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* assertain: number of unknowns = number of equations */ | |||
length(x)=length(equs), pred; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text= | |||
[[Datei:Schema-5-2-.png|rahmenlos]] | |||
Effiziente Löser für Systeme linearer Gleichungen implementieren gewöhnlich eine LU-Faktorisierung. Für dieses Mini-Beispiel können wir uns das anschauen: | |||
[[Datei:TkPb-16.png|mini|LU-Faktorisierung von A|alternativtext=|808x808px]] | |||
Und die Lösung ist | |||
[[Datei:TkPb-17.png|mini|Lösung aus Maxima.|alternativtext=|links|226x226px]] | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* ---------------------------------------------------- */ | |||
/* solve */ | |||
C : augcoefmatrix(equs,x); | |||
A : submatrix(C,9); | |||
b : -col(C,9); | |||
s : linsolve_by_lu(A,b); | |||
[ P, L, U] : get_lu_factors(lu_factor(A)); | |||
/* print results */ | |||
subst(geom,s[1]); | |||
</syntaxhighlight> | |||
}} | |||
<br clear="all"/> | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
[[Datei:Schema-6-2-.png|rahmenlos]] | |||
Existieren Winkel von α, so dass keine Lösung möglich ist? | |||
::<math>\text{det}(\underline{\underline{A}}) = -3\cdot \text{cos}\left( \alpha\right) \cdot {{\text{sin}\left( \alpha\right) }^{2}}</math> | |||
Nur für die WInkel α=0, 90° - und die sind physikalisch nicht sinnvoll. | |||
Also:Nein! | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* ---------------------------------------------------- */ | |||
D : determinant(A); | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 9. April 2021, 09:30 Uhr
Aufgabenstellung
Ein Stabwerk aus 5 Stäben wird durch eine Kraft F belastet. Alle Stäbe haben die Länge a.
Hier soll eine einfache Stabwerksaufgabe gelöste werden - aber im Hintergrund geht es eigentlich darum, wie dieser Lösungsprozess in einer Software - hier Maxima - umgesetzt wird.
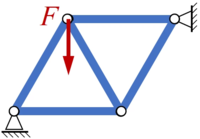
Gesucht sind die Stab- und Lagerreaktionskräfte des Systems nach dem Knotenpunktverfahren.
Lösung "per Hand" und mit Maxima
Beide Lösungsansätz verfolgen wir parallel - bis wir zur Lösung des Gleichungssystems kommen.
Header
Hier steht nur die Maxima-Headerdatei. Sie soll später helfen, die richtige Versionsnummer der Software zu finden und Ansprechpartner für Nachfragen zu identifizieren.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2016-09-18 */
/* ref: Ma-2, Unterricht zu Linearer Algebra */
/* description: solves the linear system of equs */
/* for the od forces */
/*******************************************************/
Declarations
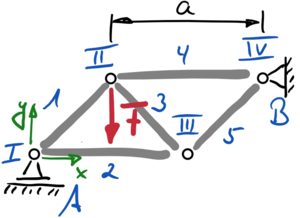
Wir nummerieren zunächst die Knoten und Stäbe, damit wir sie im weiteren Lösungsverlauf eindeutig ansprechen können.
Und ein bischen Geometrie Geometrie müssen wir auch ansetzen, um die sin- und cos-Beziehungen von α zu bekommen:
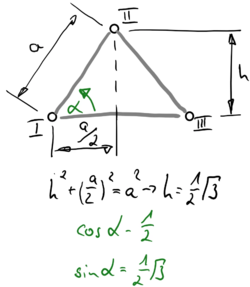
Wir setzen also
- .
Knoten I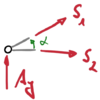 |
Knoten II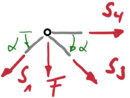 |
Knoten III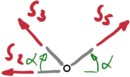 |
Knoten IV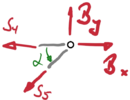 |
/* ---------------------------------------------------- */
/* geometry */
geom : [cos(alpha) = 1/2, sin(alpha) = 1/2*sqrt(3)];
Equilibrium Conditions
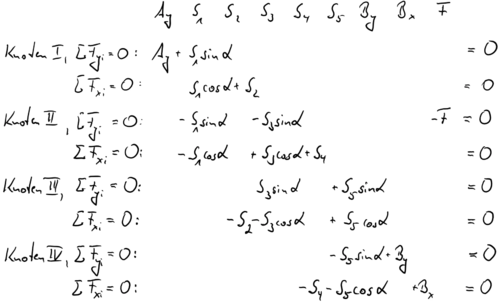
Wir schreiben je Knoten die zwei Gleichgewichtsbedingungen an, die Koeffizienten schreiben wir dabei schon mal so an, wie sie hinterher in der System-Matrix auftauchen sollen:

/* ---------------------------------------------------- */
/* equilibrium conditions at nodes */
equs : [+ A[y] + S[1]*sin(alpha) = 0,
+ S[1]*cos(alpha) + S[2] = 0,
- S[1]*sin(alpha) - S[3]*sin(alpha) - F = 0,
- S[1]*cos(alpha) + S[3]*cos(alpha) + S[4] = 0,
+ S[3]*sin(alpha) + S[5]*sin(alpha) = 0,
- S[2] - S[3]*cos(alpha) + S[5]*cos(alpha) = 0,
- S[5]*sin(alpha) + B[y] = 0,
- S[4] - S[5]*cos(alpha) + B[x] = 0];
/* unknowns */
x : [ A[y], S[1], S[2], S[3], S[4], S[5], B[y], B[x]];
Check for Solvability

Ja - so sieht es aus.
/* assertain: number of unknowns = number of equations */
length(x)=length(equs), pred;
Solving
Effiziente Löser für Systeme linearer Gleichungen implementieren gewöhnlich eine LU-Faktorisierung. Für dieses Mini-Beispiel können wir uns das anschauen:

Und die Lösung ist
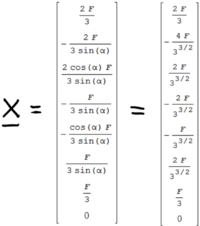
/* ---------------------------------------------------- */
/* solve */
C : augcoefmatrix(equs,x);
A : submatrix(C,9);
b : -col(C,9);
s : linsolve_by_lu(A,b);
[ P, L, U] : get_lu_factors(lu_factor(A));
/* print results */
subst(geom,s[1]);
Post-Processing
Existieren Winkel von α, so dass keine Lösung möglich ist?
Nur für die WInkel α=0, 90° - und die sind physikalisch nicht sinnvoll.
Also:Nein!
/* ---------------------------------------------------- */
D : determinant(A);
Links
- ...
Literature
- ...