Gelöste Aufgaben/T401: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 23: | Zeile 23: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text= | |||
Hauptspannungsrichtungen sind Schnittnormalen im Element, bei denen die Schubspannungen auf den Schnittflächen verschwinden. | Hauptspannungsrichtungen sind Schnittnormalen im Element, bei denen die Schubspannungen auf den Schnittflächen verschwinden. | ||
Alle Vergleichsspannungs-Hypothesen gehen von den Spannungen in den Hauptspannungsrchtungen aus. | Alle Vergleichsspannungs-Hypothesen gehen von den Spannungen in den Hauptspannungsrchtungen aus. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-11-15 */ | |||
/* ref: FEM-stress analysis */ | |||
/* description: finds the eigenvalues and */ | |||
/* eigenvectors for a stress state */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | {{MyCodeBlock|title=Declarations | ||
Für die Analyse brauchen wir die Spannungs-Dehnungs-Beziehung (Stress-Strain-Relation) für den ebenen Spannungszustand: | |text= | ||
Für die Analyse brauchen wir die [[Sources/Lexikon/Spannungs-Dehnungs-Beziehung (Stress-Strain-Relation)|Spannungs-Dehnungs-Beziehung (Stress-Strain-Relation)]] für den ebenen Spannungszustand: | |||
::<math>\underline{\sigma} = \underline{\underline{E}}\cdot \underline{\varepsilon}</math> mit | |||
::<math>\displaystyle \underline{\underline{E}}=\frac{E}{1-\nu^2}\begin{pmatrix}1 & \nu & 0\\ \nu & 1 & 0\\ 0 & 0 & \left( 1-\nu\right) \end{pmatrix}</math>. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /* parameter */ | ||
field: [e[x,x]=1/800,e[y,y]=-1/800,e[y,x]=e[x,y]/4,e[x,y]=-sqrt(3)/500]; | |||
Epsilon : E/(1-nu^2)*funmake('matrix,[[1,nu,0],[nu,1,0],[0,0,1-nu]]); | |||
print('Epsilon = Epsilon)$ | |||
use : [nu=(1/4), E=10^5*N/mm^2, sigma[x,x]=100*N/mm^2]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | {{MyCodeBlock|title=Displacement Field | ||
|text= | |||
[[Datei:T401-11.png|mini|Verformtes Element]]Das Verschiebungsfeld erfasst, wie sich die materiellen Punkte des Finiten Elements verschieben. | [[Datei:T401-11.png|mini|Verformtes Element]]Das Verschiebungsfeld erfasst, wie sich die materiellen Punkte des Finiten Elements verschieben. | ||
Wir können damit das Finite Element in seinem Ausgangszustand (grau) und im verformten Zustand (blau, hier mit 20-facher Verzerrung dargestellt) plotten: | Wir können damit das Finite Element in seinem Ausgangszustand (grau) und im verformten Zustand (blau, hier mit 20-facher Verzerrung dargestellt) plotten: | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* plot displacement field */ | ||
magnif: makelist(lhs(field[i]) = 20*rhs(field[i]),i,1,4); | |||
params: append([u[0] = 0.3, v[0] = 0.1], magnif); | |||
W : [u[0]+e[x,x]*x + e[x,y]*y, | |||
v[0]+e[y,x]*x + e[y,y]*y]; | |||
path: [[x=t,y=0],[x=1,y=t],[x=t,y=1],[x=0,y=t]]; | |||
lister: [makelist([parametric, subst(path[i],x ), subst(path[i],y )],i,1,4), | |||
makelist([parametric, subst(path[i],x+subst(params,W[1])), subst(path[i],y+subst(params,W[2]))],i,1,4)]; | |||
lister: subst(params,append(lister[1],lister[2])); | |||
plot2d(lister,[t,0,1], [x,-0.5,1.5], [y,-0.5,1.5],[yx_ratio, 1], | |||
[color, gray, gray, gray, gray, blue, blue, blue, blue], | |||
[style, [lines,1], [lines,1], [lines,1], [lines,1], [lines,3], [lines,3], [lines,3], [lines,3]], | |||
[legend,false], [xlabel, "x/mm ->"], [ylabel, "y/mm ->"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | |||
{{MyCodeBlock|title=Eigenvalues and -vectors | |||
|text= | |||
Für die Berechnungen der Spannungen brauchen wir zuerst die Dehnungen, die wir aus den [[Sources/Lexikon/Verzerrungs-Verschiebungs-Beziehung (Strain-Displacement-Relation)|Verzerrungs-Verschiebungs-Beziehung (Strain-Displacement-Relation)]] | Für die Berechnungen der Spannungen brauchen wir zuerst die Dehnungen, die wir aus den [[Sources/Lexikon/Verzerrungs-Verschiebungs-Beziehung (Strain-Displacement-Relation)|Verzerrungs-Verschiebungs-Beziehung (Strain-Displacement-Relation)]] | ||
<math>\displaystyle \varepsilon_{i,j} = \frac{1}{2}\left( \frac{du_i}{dx_j}+\frac{du_j}{dx_i}\right)</math> | ::<math>\displaystyle \varepsilon_{i,j} = \frac{1}{2}\left( \frac{du_i}{dx_j}+\frac{du_j}{dx_i}\right)</math> | ||
zu | zu | ||
<math>\underline{\underline{\epsilon}}=\begin{pmatrix}{{e}_{x,x}} & \displaystyle \frac{{{e}_{x,y}}+{{e}_{y,x}}}{2}\\ \displaystyle \frac{{{e}_{x,y}}+{{e}_{y,x}}}{2} & {{e}_{y,y}}\end{pmatrix}</math> | ::<math>\underline{\underline{\epsilon}}=\begin{pmatrix}{{e}_{x,x}} & \displaystyle \frac{{{e}_{x,y}}+{{e}_{y,x}}}{2}\\ \displaystyle \frac{{{e}_{x,y}}+{{e}_{y,x}}}{2} & {{e}_{y,y}}\end{pmatrix}</math> | ||
erhalten. Die sind hier konstant, weil wir mit linearen Verschiebungsansätzen arbeiten. Umsortieren liefert die Dehnung als Spaltenmatrix, | erhalten. Die sind hier konstant, weil wir mit linearen Verschiebungsansätzen arbeiten. Umsortieren liefert die Dehnung als Spaltenmatrix, | ||
<math>\underline{\varepsilon} = \begin{pmatrix}{{e}_{x,x}}\\ {{e}_{y,y}}\\ \displaystyle \frac{{{e}_{x,y}}+{{e}_{y,x}}}{2}\end{pmatrix}</math>, | ::<math>\underline{\varepsilon} = \begin{pmatrix}{{e}_{x,x}}\\ {{e}_{y,y}}\\ \displaystyle \frac{{{e}_{x,y}}+{{e}_{y,x}}}{2}\end{pmatrix}</math>, | ||
die wir die in die Spannungs-Dehnungs-Beziehung (oben) einsetzen können. Wir finden: | die wir die in die Spannungs-Dehnungs-Beziehung (oben) einsetzen können. Wir finden: | ||
<math>\underline{\sigma}=\left(\begin{array}{l}+100\\ -100\\ -100\cdot \sqrt{3}\end{array}\right)\cdot\displaystyle \frac{ N}{{{\text{mm}}^{2}}}</math>. | ::<math>\underline{\sigma}=\left(\begin{array}{l}+100\\ -100\\ -100\cdot \sqrt{3}\end{array}\right)\cdot\displaystyle \frac{ N}{{{\text{mm}}^{2}}}</math>. | ||
Diese schreiben wir wieder nun wieder um in Matrixform - als Koeffizienten des Spannungstensors, also | Diese schreiben wir wieder nun wieder um in Matrixform - als Koeffizienten des Spannungstensors, also | ||
<math>\underline{\underline{\sigma}} = 100\cdot \begin{pmatrix}1 & -\sqrt{3}\\ -\sqrt{3} & -1\end{pmatrix} \displaystyle \frac{N}{mm^2}</math>. | ::<math>\underline{\underline{\sigma}} = 100\cdot \begin{pmatrix}1 & -\sqrt{3}\\ -\sqrt{3} & -1\end{pmatrix} \displaystyle \frac{N}{mm^2}</math>. | ||
Die Hauptspannungen sind die Eigenwerte (vgl. [[Werkzeuge/Lösungsbausteine der Mathematik/Eigenwertprobleme|Eigenwertprobleme]]) des Spannungstensors, die Hauptspannungsrichtungen sind die Eigenvektoren des Spannungstensors: | Die Hauptspannungen sind die Eigenwerte (vgl. [[Werkzeuge/Lösungsbausteine der Mathematik/Eigenwertprobleme|Eigenwertprobleme]]) des Spannungstensors, die Hauptspannungsrichtungen sind die Eigenvektoren des Spannungstensors: | ||
<math>\hat{\sigma}_1 = +200 \displaystyle \frac{N}{\text{mm}^2} \text{ mit } \underline{n}_1 = \left(\begin{array}{c}\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\end{array}\right)</math> und | ::<math>\hat{\sigma}_1 = +200 \displaystyle \frac{N}{\text{mm}^2} \text{ mit } \underline{n}_1 = \left(\begin{array}{c}\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\end{array}\right)</math> und | ||
<math>\hat{\sigma}_2 = - 200 \displaystyle \frac{N}{\text{mm}^2} \text{ mit } \underline{n}_2 = \left(\begin{array}{c}\frac{1}{2}\\\frac{1}{2}\sqrt{3}\end{array}\right)</math> | ::<math>\hat{\sigma}_2 = - 200 \displaystyle \frac{N}{\text{mm}^2} \text{ mit } \underline{n}_2 = \left(\begin{array}{c}\frac{1}{2}\\\frac{1}{2}\sqrt{3}\end{array}\right)</math> | ||
Die dritte Hauptspannung ist in diesem Fall - für den ebenen Spannungszustand - | Die dritte Hauptspannung ist in diesem Fall - für den ebenen Spannungszustand - | ||
<math>\hat{\sigma}_3 = 0</math>. | ::<math>\hat{\sigma}_3 = 0</math>. | ||
Statt das Eigenwertproblem zu lösen, können wir auch den [[Sources/Lexikon/Mohrscher Spannungskreis|Mohrschen Spannungskreis]] einsetzen. Für numerische Anwendungen wie FEM ist diese Sichtweise aber nicht zweckmäßig.[[Datei:T401-21.png|mini|Hauptspannungen]]Eigenvektoren und Eigenwerte können wir nun im Element auftragen: | Statt das Eigenwertproblem zu lösen, können wir auch den [[Sources/Lexikon/Mohrscher Spannungskreis|Mohrschen Spannungskreis]] einsetzen. Für numerische Anwendungen wie FEM ist diese Sichtweise aber nicht zweckmäßig.[[Datei:T401-21.png|mini|Hauptspannungen]]Eigenvektoren und Eigenwerte können wir nun im Element auftragen: | ||
| Zeile 95: | Zeile 123: | ||
Die Vergleichsspannung für die Formulierung mit den Hypothese von "von Mises" ist | Die Vergleichsspannung für die Formulierung mit den Hypothese von "von Mises" ist | ||
<math>\displaystyle \sigma_V = \frac{1}{\sqrt{2}} \sqrt{ \left(\hat{\sigma}_1-\hat{\sigma}_2\right)^2+\left(\hat{\sigma}_2-\hat{\sigma}_3\right)^2+\left(\hat{\sigma}_1-\hat{\sigma}_3\right)^2}</math>, | ::<math>\displaystyle \sigma_V = \frac{1}{\sqrt{2}} \sqrt{ \left(\hat{\sigma}_1-\hat{\sigma}_2\right)^2+\left(\hat{\sigma}_2-\hat{\sigma}_3\right)^2+\left(\hat{\sigma}_1-\hat{\sigma}_3\right)^2}</math>, | ||
also | also | ||
<math>\sigma_V \approx 350 \frac{N}{mm^2}</math>. | ::<math>\sigma_V \approx 350 \frac{N}{mm^2}</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /* compute strains */ | ||
epsilon: makelist(makelist( | |||
1/2*(diff(W[i],[x,y][j])+diff(W[j],[x,y][i])), | |||
i,1,2),j,1,2); | |||
print('epsilon ,"=", funmake('matrix,epsilon))$ | |||
/* compute stresses */ | |||
Sigma : Epsilon.funmake('matrix,[[epsilon[1][1]],[epsilon[2][2]],[epsilon[1][2]]]); | |||
print('Sigma = subst(use,subst(field,Sigma)))$ | |||
/* coefficients of stress tensor */ | |||
Sigma : funmake('matrix,[[Sigma[1][1],Sigma[3][1]],[Sigma[3][1],Sigma[2][1]]]); | |||
load(eigen)$ | |||
system: uniteigenvectors (subst(use,subst(field,Sigma))); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | ===FEM-Results=== | ||
Auftragen der Verschiebungsfelder aller Finiten Elemente liefert folgendes Bild - wobei wir die Flächen nach dem Betrag der Verschiebung einfärben: | Auftragen der Verschiebungsfelder aller Finiten Elemente liefert folgendes Bild - wobei wir die Flächen nach dem Betrag der Verschiebung einfärben: | ||
<table class="wikitable" style="background-color:white;"> | |||
<tr> | |||
<td>[[Datei:T401-Verschiebungen-Legende.png|mini|150px|Legende|ohne]]</td> | |||
<td>[[Datei:T401-Verschiebungen.png|mini|150px|Verschiebungen der Knoten|ohne]]</td></tr> | |||
</table> | |||
[[Datei:T401-Hauptspannungen.png|mini|Hauptspannungen]]Und wir können können für jedes Finite Element die Hauptspannungen und deren Richtungen grafisch darstellen: | [[Datei:T401-Hauptspannungen.png|mini|Hauptspannungen]]Und wir können können für jedes Finite Element die Hauptspannungen und deren Richtungen grafisch darstellen: | ||
| Zeile 116: | Zeile 161: | ||
Dabei sind die Pfeile der Hauptspannungen in ANSYS so sortiert, dass | Dabei sind die Pfeile der Hauptspannungen in ANSYS so sortiert, dass | ||
<math>\begin{array}{ll}\hat{\sigma}_1 &\ldots \text{rot}\\\hat{\sigma}_2 &\ldots \text{grün}\\\hat{\sigma}_3 &\ldots \text{blau}\end{array}</math> | ::<math>\begin{array}{ll}\hat{\sigma}_1 &\ldots \text{rot}\\\hat{\sigma}_2 &\ldots \text{grün}\\\hat{\sigma}_3 &\ldots \text{blau}\end{array}</math> | ||
mit | mit | ||
<math>\hat{\sigma}_1>\hat{\sigma}_2>\hat{\sigma}_3</math>. | ::<math>\hat{\sigma}_1>\hat{\sigma}_2>\hat{\sigma}_3</math>. | ||
{{MyTip|title=Seltsam?|text=Hier ist übrigens im ganzen Bauteil eine der Hauptspannungen Null! | {{MyTip|title=Seltsam?|text=Hier ist übrigens im ganzen Bauteil eine der Hauptspannungen Null! | ||
<br/> | |||
Warum?}} | |||
== | ==Stress-Flow Analogy== | ||
[[Datei:T401-Hauptspannungen-Fluss+.png|mini|Spannungsfluss-Analogie]]Die Hauptspannungsrichtungen sind Grundlage für die "Strömungsanalogie" der Festkörpermechanik. Wir können uns die Spannung als "Fluss" entland der Verbindungen aller Hauptspannugnsrichtungen vorstellen. Die Pfeil-Länge ist dabei proportional zum Betrag der Hauptspannung. | [[Datei:T401-Hauptspannungen-Fluss+.png|mini|Spannungsfluss-Analogie]]Die Hauptspannungsrichtungen sind Grundlage für die "Strömungsanalogie" der Festkörpermechanik. Wir können uns die Spannung als "Fluss" entland der Verbindungen aller Hauptspannugnsrichtungen vorstellen. Die Pfeil-Länge ist dabei proportional zum Betrag der Hauptspannung. | ||
Verbinden wir die Pfeile der maximalen Hauptspannung im Bild, erhalten wir dieses Bild, das zeigt, wie die Spannung um die Kante herum "fließt". | Verbinden wir die Pfeile der maximalen Hauptspannung im Bild, erhalten wir dieses Bild, das zeigt, wie die Spannung um die Kante herum "fließt". | ||
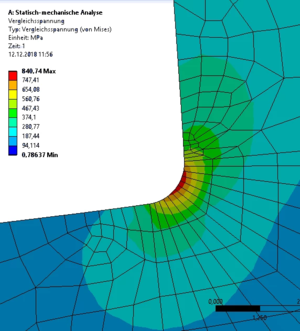
Und wir können die Vergleichsspannung im Bauteil berechenen - hier nach der Gestaltänderungshypothese (von Mises): | Und wir können die Vergleichsspannung im Bauteil berechenen - hier nach der Gestaltänderungshypothese (von Mises): | ||
<table class="wikitable" style="background-color:white; | <table class="wikitable" style="background-color:white;"> | ||
"> | <tr> | ||
< | <td>[[Datei:T401-Spannungen.png|mini|Spannungen|ohne]]</td> | ||
<td>[[Datei:T401-Spannungen-2.png|mini|Vergleichsspannung im kritischen Bereich|ohne]] | |||
</td></tr> | |||
</table> | </table> | ||
<hr /> | <hr /> | ||
| Zeile 158: | Zeile 193: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 6. April 2021, 17:55 Uhr
Aufgabenstellung
Wie ein FE-Programm die Hauptspannungen aus dem Verschiebungsfeld berechnet und wie wir das Feld der Hauptspannungen im Gebiet zur Interpretation des "Spannungsflusses" nutzen, beschreibt dieses gelöste Problem.
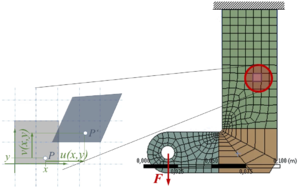
Bei der Analyse eines ebenen Bauteils wird der Verschiebungszustand eines Finiten Elementes durch
erfasst.
Gesucht sind die Hauptspannungen und Hauptspannungs-Richtungen im Finiten Element.
Dabei werden die Koeffizienten des Verschiebungsfeldes mit
angegeben. Die Material-Parameter sind
,
das Finite Elemente hat eine Kantenlänge von jeweils 1 mm.
Lösung mit Maxima
Header
Hauptspannungsrichtungen sind Schnittnormalen im Element, bei denen die Schubspannungen auf den Schnittflächen verschwinden.
Alle Vergleichsspannungs-Hypothesen gehen von den Spannungen in den Hauptspannungsrchtungen aus.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-11-15 */
/* ref: FEM-stress analysis */
/* description: finds the eigenvalues and */
/* eigenvectors for a stress state */
/*******************************************************/
Declarations
Für die Analyse brauchen wir die Spannungs-Dehnungs-Beziehung (Stress-Strain-Relation) für den ebenen Spannungszustand:
- mit
- .
/* parameter */
field: [e[x,x]=1/800,e[y,y]=-1/800,e[y,x]=e[x,y]/4,e[x,y]=-sqrt(3)/500];
Epsilon : E/(1-nu^2)*funmake('matrix,[[1,nu,0],[nu,1,0],[0,0,1-nu]]);
print('Epsilon = Epsilon)$
use : [nu=(1/4), E=10^5*N/mm^2, sigma[x,x]=100*N/mm^2];
Displacement Field
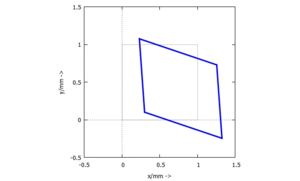
Das Verschiebungsfeld erfasst, wie sich die materiellen Punkte des Finiten Elements verschieben.
Wir können damit das Finite Element in seinem Ausgangszustand (grau) und im verformten Zustand (blau, hier mit 20-facher Verzerrung dargestellt) plotten:
/* plot displacement field */
magnif: makelist(lhs(field[i]) = 20*rhs(field[i]),i,1,4);
params: append([u[0] = 0.3, v[0] = 0.1], magnif);
W : [u[0]+e[x,x]*x + e[x,y]*y,
v[0]+e[y,x]*x + e[y,y]*y];
path: [[x=t,y=0],[x=1,y=t],[x=t,y=1],[x=0,y=t]];
lister: [makelist([parametric, subst(path[i],x ), subst(path[i],y )],i,1,4),
makelist([parametric, subst(path[i],x+subst(params,W[1])), subst(path[i],y+subst(params,W[2]))],i,1,4)];
lister: subst(params,append(lister[1],lister[2]));
plot2d(lister,[t,0,1], [x,-0.5,1.5], [y,-0.5,1.5],[yx_ratio, 1],
[color, gray, gray, gray, gray, blue, blue, blue, blue],
[style, [lines,1], [lines,1], [lines,1], [lines,1], [lines,3], [lines,3], [lines,3], [lines,3]],
[legend,false], [xlabel, "x/mm ->"], [ylabel, "y/mm ->"])$
Eigenvalues and -vectors
Für die Berechnungen der Spannungen brauchen wir zuerst die Dehnungen, die wir aus den Verzerrungs-Verschiebungs-Beziehung (Strain-Displacement-Relation)
zu
erhalten. Die sind hier konstant, weil wir mit linearen Verschiebungsansätzen arbeiten. Umsortieren liefert die Dehnung als Spaltenmatrix,
- ,
die wir die in die Spannungs-Dehnungs-Beziehung (oben) einsetzen können. Wir finden:
- .
Diese schreiben wir wieder nun wieder um in Matrixform - als Koeffizienten des Spannungstensors, also
- .
Die Hauptspannungen sind die Eigenwerte (vgl. Eigenwertprobleme) des Spannungstensors, die Hauptspannungsrichtungen sind die Eigenvektoren des Spannungstensors:
- und
Die dritte Hauptspannung ist in diesem Fall - für den ebenen Spannungszustand -
- .
Statt das Eigenwertproblem zu lösen, können wir auch den Mohrschen Spannungskreis einsetzen. Für numerische Anwendungen wie FEM ist diese Sichtweise aber nicht zweckmäßig.
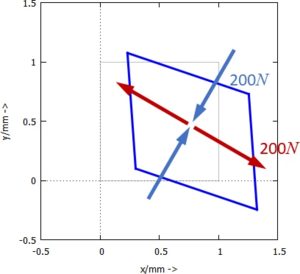
Eigenvektoren und Eigenwerte können wir nun im Element auftragen:
Die Vergleichsspannung für die Formulierung mit den Hypothese von "von Mises" ist
- ,
also
- .
/* compute strains */
epsilon: makelist(makelist(
1/2*(diff(W[i],[x,y][j])+diff(W[j],[x,y][i])),
i,1,2),j,1,2);
print('epsilon ,"=", funmake('matrix,epsilon))$
/* compute stresses */
Sigma : Epsilon.funmake('matrix,[[epsilon[1][1]],[epsilon[2][2]],[epsilon[1][2]]]);
print('Sigma = subst(use,subst(field,Sigma)))$
/* coefficients of stress tensor */
Sigma : funmake('matrix,[[Sigma[1][1],Sigma[3][1]],[Sigma[3][1],Sigma[2][1]]]);
load(eigen)$
system: uniteigenvectors (subst(use,subst(field,Sigma)));
FEM-Results
Auftragen der Verschiebungsfelder aller Finiten Elemente liefert folgendes Bild - wobei wir die Flächen nach dem Betrag der Verschiebung einfärben:
 |
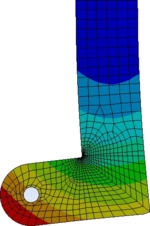 |
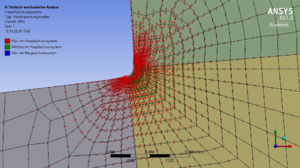
Und wir können können für jedes Finite Element die Hauptspannungen und deren Richtungen grafisch darstellen:
Dabei sind die Pfeile der Hauptspannungen in ANSYS so sortiert, dass
mit
- .
| ✔ Seltsam?: |
| Hier ist übrigens im ganzen Bauteil eine der Hauptspannungen Null!
|
Stress-Flow Analogy
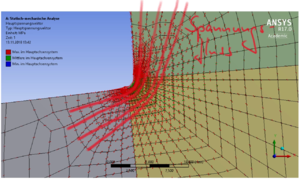
Die Hauptspannungsrichtungen sind Grundlage für die "Strömungsanalogie" der Festkörpermechanik. Wir können uns die Spannung als "Fluss" entland der Verbindungen aller Hauptspannugnsrichtungen vorstellen. Die Pfeil-Länge ist dabei proportional zum Betrag der Hauptspannung.
Verbinden wir die Pfeile der maximalen Hauptspannung im Bild, erhalten wir dieses Bild, das zeigt, wie die Spannung um die Kante herum "fließt".
Und wir können die Vergleichsspannung im Bauteil berechenen - hier nach der Gestaltänderungshypothese (von Mises):
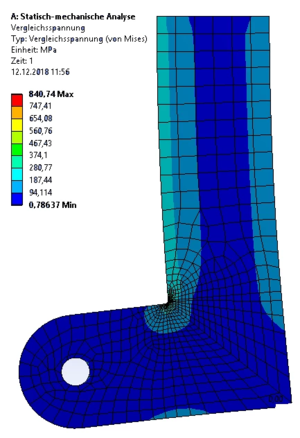 |
 |
Links
- ...
Literature
- ...
















