Gelöste Aufgaben/SKEB: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 20: | Zeile 20: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
= | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | |||
|text= | |||
Für die mathematische Behandlung - insbesondere der Auflösung quadratischer Gleichungen - setzen wir in Maxima voraus, dass | Für die mathematische Behandlung - insbesondere der Auflösung quadratischer Gleichungen - setzen wir in Maxima voraus, dass | ||
<math>E > 0,\;\;\;I>0,\;\;\;\ell_0>0,\;\;\;\varrho>0;</math>. | ::<math>E > 0,\;\;\;I>0,\;\;\;\ell_0>0,\;\;\;\varrho>0;</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*******************************************************/ | ||
/* MAXIMA script */ | |||
/* version: wxMaxima 16.04.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-01-15 */ | |||
/* ref: oscillations of continuous media */ | |||
/* description: analytic solutioun for EBB */ | |||
/*******************************************************/ | |||
/* settings */ | |||
workdir: "C:\\Users\\X...X\\plots\\"; | |||
/* assumptions */ | |||
assume(rho>0, E>0,I>0,A>0,l[0]>0,alpha>0,gamma>0); | |||
/* abbreviations used later .... */ | |||
abbrev : [alpha = (sqrt(omega[0])*A^(1/4)*rho^(1/4)*l[0])/(E^(1/4)*I^(1/4)), | |||
gamma = ((cosh(alpha)+cos(alpha)))/(sinh(alpha)+sin(alpha))]; | |||
abbrev : append(abbrev, solve(abbrev,[sqrt(omega[0]),cosh(alpha)])[1]); | |||
abbrev : append(abbrev, [abbrev[3]^2,abbrev[3]^3]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Equations of Motion | |||
In der Gleichgewichtsbeziehung für den Euler-Bernoulli-Balken setzen wir als eingeprägte, äußere Streckenlast ''q(x,t)'' die [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'sche Trägheitskraft]] und die Gewichtskraft an, also | |text= | ||
In der Gleichgewichtsbeziehung für den [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] setzen wir als eingeprägte, äußere Streckenlast ''q(x,t)'' die [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'sche Trägheitskraft]] und die Gewichtskraft an, also | |||
<math>q(x,t) = \varrho\;A\cdot g -\varrho\;A\cdot \ddot{w}(x,t)</math> | ::<math>q(x,t) = \varrho\;A\cdot g -\varrho\;A\cdot \ddot{w}(x,t)</math> | ||
Die Lösung der linearen, partielle Bewegungsgleichung | Die Lösung der linearen, partielle Bewegungsgleichung | ||
<math>\varrho\,A\cdot\ddot{w}+E\,I\cdot{w}^{IV} = \varrho\,A\cdot g</math> | ::<math>\varrho\,A\cdot\ddot{w}+E\,I\cdot{w}^{IV} = \varrho\,A\cdot g</math> | ||
setzt sich dann aus zwei Lösungsanteilen, der partikularen Lösung ''w<sub>p</sub>'' und der homogenen Lösung ''w<sub>h</sub>'', zusammen; wir schreiben | setzt sich dann aus zwei Lösungsanteilen, der partikularen Lösung ''w<sub>p</sub>'' und der homogenen Lösung ''w<sub>h</sub>'', zusammen; wir schreiben | ||
<math>w_t(x,t) = w_p(x,t) + w_h(x,t) </math>. | ::<math>w_t(x,t) = w_p(x,t) + w_h(x,t) </math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/* equation of motion */ | |||
eom: rho*A*diff(w(x,t),t,2) + E*I*diff(w(x,t),x,4) = rho*A*g; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Particular Solution | |||
|text= | |||
Die partikulare Lösung ''w<sub>p</sub>'' erfüllt die "rechte Seite" der Bewegungsgleichung, also ''ϱ A⋅g'': | Die partikulare Lösung ''w<sub>p</sub>'' erfüllt die "rechte Seite" der Bewegungsgleichung, also ''ϱ A⋅g'': | ||
<math>E\,I\cdot{w}_p^{IV} = \varrho\,A\cdot g</math>. | ::<math>E\,I\cdot{w}_p^{IV} = \varrho\,A\cdot g</math>. | ||
Die rechte Seite ist zeit-unveränderlich - so auch die partikulare Lösung. | Die rechte Seite ist zeit-unveränderlich - so auch die partikulare Lösung. | ||
| Zeile 67: | Zeile 84: | ||
Wir integrieren die Bewegungsgleichung vier Mal und erhalten | Wir integrieren die Bewegungsgleichung vier Mal und erhalten | ||
<math>\displaystyle E\,I\,w\left( x,t\right) =\frac{A\,g\,\rho{{x}^{4}}}{24}+{{C}_{3}}\,\frac{{{x}^{3}}}{6}+{{C}_{2}}\,\frac{{{x}^{2}}}{2}+{{C}_{1}}\,x+{{C}_{0}}</math>. | ::<math>\displaystyle E\,I\,w\left( x,t\right) =\frac{A\,g\,\rho{{x}^{4}}}{24}+{{C}_{3}}\,\frac{{{x}^{3}}}{6}+{{C}_{2}}\,\frac{{{x}^{2}}}{2}+{{C}_{1}}\,x+{{C}_{0}}</math>. | ||
Die vier Integrationskonstanten ''C<sub>i</sub>'' müssen wir nun an die Randbedingungen | Die vier Integrationskonstanten ''C<sub>i</sub>'' müssen wir nun an die Randbedingungen | ||
<math>\begin{array}{rl}w_p(0)&=0\\w_p'(0)&=0\\E\,I\,w_p''(\ell)&=0\\E\,I\,w_p'''(\ell)&=0\end{array}</math> | ::<math>\begin{array}{rl}w_p(0)&=0\\w_p'(0)&=0\\E\,I\,w_p''(\ell)&=0\\E\,I\,w_p'''(\ell)&=0\end{array}</math> | ||
anpassen, wir erhalten mit dem linearen Gleichungssystem | anpassen, wir erhalten mit dem linearen Gleichungssystem | ||
<math>\begin{array}{l}0 = {{C}_{0}}\\ 0={{C}_{1}}\\ 0=\frac{{{\ell}_{0}^{2}}Ag\rho}{2}+{{\ell}_{0}}\,{{C}_{3}}+{{C}_{2}}\\ 0={{\ell}_{0}}Ag\rho+{{C}_{3}}\end{array}</math> | ::<math>\begin{array}{l}0 = {{C}_{0}}\\ 0={{C}_{1}}\\ 0=\frac{{{\ell}_{0}^{2}}Ag\rho}{2}+{{\ell}_{0}}\,{{C}_{3}}+{{C}_{2}}\\ 0={{\ell}_{0}}Ag\rho+{{C}_{3}}\end{array}</math> | ||
die partikulare Lösung | die partikulare Lösung | ||
<math>\displaystyle E\,I\,{w}_p\left( x\right) =A\,g\,\varrho \,\ell^4 \cdot\left(\frac{{{\xi}^{4}}}{24}-\frac{{{\xi}^{3}}}{6}+\frac{{{\xi}^{2}}}{4}\right)</math>.[[Datei:UEBE-11.png|mini|Statische Auslenkung]]Die maximale Auslenkung - am rechten Rand - nutzen wir als Bezugslänge | ::<math>\displaystyle E\,I\,{w}_p\left( x\right) =A\,g\,\varrho \,\ell^4 \cdot\left(\frac{{{\xi}^{4}}}{24}-\frac{{{\xi}^{3}}}{6}+\frac{{{\xi}^{2}}}{4}\right)</math>. | ||
[[Datei:UEBE-11.png|mini|Statische Auslenkung]]Die maximale Auslenkung - am rechten Rand - nutzen wir als Bezugslänge | |||
<math>\displaystyle {{w}_{s}}=\frac{{{\ell}^{4}}\,A\,g\,\rho}{8\,E\,I}</math> | ::<math>\displaystyle {{w}_{s}}=\frac{{{\ell}^{4}}\,A\,g\,\rho}{8\,E\,I}</math> | ||
Und so sieht ''w<sub>p</sub>'' aus: | Und so sieht ''w<sub>p</sub>'' aus: | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/***************************************************************************/ | |||
/* p a r t i c u l a r s o l u t i o n */ | |||
/***************************************************************************/ | |||
peom : subst(['diff(w(x,t),t,2)=0],eom); | |||
w[p] : integrate(integrate(integrate(integrate(peom,x),x),x),x); | |||
w[p] : subst([%c1=C[3],%c2=C[2],%c3=C[1],%c4=C[0]],w[p]); | |||
BouCon : [subst([x= 0 ],subst([ w(x,t) =0], w[p] )), | |||
subst([x= 0 ],subst(['diff(w(x,t),x,1)=0],diff(w[p],x,1))), | |||
subst([x=l[0]],subst(['diff(w(x,t),x,2)=0],diff(w[p],x,2))), | |||
subst([x=l[0]],subst(['diff(w(x,t),x,3)=0],diff(w[p],x,3)))]; | |||
w[p] : subst(solve(BouCon,makelist(C[i],i,0,3))[1],w[p]); | |||
w[p] : ratsimp(lhs(w[p]/(E*I)) = subst([x=l[0]*xi], rhs(w[p])/(E*I))); | |||
params: [w[s] = subst([xi=1],subst(w[p],w(x,t))), omega[0]=2*%pi/T]; | |||
plot2d(ratsimp(subst(params,subst(w[p],w(x,t))/w[s])),[xi,0,1], | |||
[legend, "w[p]/w[s]"], | |||
[style, [lines,3,1]], [xlabel, "ξ →"], [ylabel, "← w"], | |||
[gnuplot_preamble, "set yrange [1.1:-0.1] reverse"])$ | |||
1 | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Homogeneous Solution | |||
|text= | |||
Die homogene Bewegungsgleichung | |||
::<math>\varrho\,A\cdot\ddot{w}+E\,I\cdot{w}^{IV} = 0</math> | |||
lässt Lösungen vom Typ | |||
::<math>\displaystyle {w}_h\left( x,t\right) ={\hat{W}}\cdot {e}^{\kappa\,x} \cdot {e}^{j \,\omega_0\,t} \;\;\;\text{ mit }\;\;\; j=\sqrt{-1}</math> | |||
zu. Wir bekommen zu jedem ''ω<sub>0</sub>'' vier ''κ'' | |||
::<math>\begin{array}{l} \displaystyle \kappa_1=+\frac{j\,\alpha}{\ell},\\ \displaystyle \kappa_2=-\frac{\alpha}{\ell},\\ \displaystyle \kappa_3=-\frac{j\,\alpha}{\ell},\\ \displaystyle \kappa_4=+\frac{\alpha}{\ell} \end{array} \;\;\text{ mit }\;\;\displaystyle\alpha^4 = \frac{{{\ell}^{4}}\,A\,\rho}{E\,I}\cdot {{\omega}_{0}^{2}}</math>, | |||
also | |||
::<math>w_h(x,t) = \left({\hat{W}_{1}}\,{{e}^{\displaystyle \frac{j\,\alpha\,x}{\ell}}}+{\hat{W}_{3}}\,{{e}^{\displaystyle -\frac{j\,\alpha\,x}{\ell}}}+{\hat{W}_{4}}\,{{e}^{\displaystyle \frac{\alpha x}{\ell}}}+{\hat{W}_{2}}\,{{e}^{\displaystyle -\frac{\alpha x}{\ell}}}\right) \cdot e^{\displaystyle j\;\omega_0\,t}</math> | |||
Die komplexen Exponenten deuten schon darauf hin: im Allgemeinen sind die Koeffizienten ''W<sub>i</sub>'' ebenfalls komplex. Für dieses Beispiel macht es deshalb viel Sinn, diese allgemeine Lösung der homogenen Differentialgleichung etwas anders hinzuschreiben. Wir nutzen dafür: | |||
<ul> | |||
<li>die [https://de.wikipedia.org/wiki/Hyperbelfunktion Hyperbelfunktionen]<br/> | |||
::<math>\begin{array}{l}\displaystyle \sinh(z)={\frac {e^{z}-e^{-z}}{2}}\\\displaystyle \cosh(z)={\frac {e^{z}+e^{-z}}{2}}\end{array}</math></li> | |||
<li>die [https://de.wikipedia.org/wiki/Eulersche_Formel Euler'sche Formel]<br/> | |||
::<math>\displaystyle e^{j \,z} = \cos(z) + j\cdot\sin(z)</math></li> | |||
</ul> | |||
Dann lautet die allgemeine Lösung | |||
::<math>\displaystyle {w}\left( x,t\right) =\left( {{W}_{1}}\,{\sinh}\left( \frac{\alpha\,x}{\ell}\right) +{{W}_{2}}\,\cosh{\left( \frac{\alpha\,x}{\ell}\right) }+{{W}_{3}}\,\sin{\left( \frac{\alpha\,x}{\ell}\right) }+{{W}_{4}}\,\cos{\left( \frac{\alpha\,x}{\ell}\right) }\right)\cdot {{e}^{\displaystyle j\,{{\omega}_{0}}\,t}}</math>, | |||
bei der wir davon ausgehen dürfen, dass alle ''W<sub>i</sub>'' reellwertig sind. | |||
Wie bei der partikularen Lösung ''w<sub>p</sub>'' sind es die vier Integrationskonstanten ''W<sub>i</sub>'', die wir nun an die Randbedingungen | |||
::<math>\begin{array}{rl}w_h(0,t)&=0\\w_h'(0,t)&=0\\E\,I\,w_h''(\ell,t)&=0\\E\,I\,w_h'''(\ell,t)&=0\end{array}</math> | |||
anpassen müssen. Wir erhalten das lineare Gleichungssystem | |||
::<math>\begin{array}{ccc} \displaystyle {{W}_{2}}+{{W}_{4}}&=&0,\\ \displaystyle \frac{{{W}_{1}}\alpha}{\ell}+\frac{{{W}_{3}}\alpha}{\ell}&=&0,\\ \displaystyle \frac{{{W}_{1}}\,{{\alpha}^{2}}\,{\sinh}\left( \alpha\right) }{{\ell^{2}}}+\frac{{{W}_{2}}\,{{\alpha}^{2}}\,\cosh{\left( \alpha\right) }}{{\ell^{2}}}-\frac{{{W}_{3}}\,{{\alpha}^{2}}\,\sin{\left( \alpha\right) }}{{\ell^{2}}}-\frac{{{W}_{4}}\,{{\alpha}^{2}}\,\cos{\left( \alpha\right) }}{{\ell^{2}}}&=&0,\\ \displaystyle \frac{{{W}_{1}}\,{{\alpha}^{3}}\,\cosh{\left( \alpha\right) }}{{\ell^{3}}}+\frac{{{W}_{2}}\,{{\alpha}^{3}}\,{\sinh}\left( \alpha\right) }{{\ell^{3}}}-\frac{{{W}_{3}}\,{{\alpha}^{3}}\,\cos{\left( \alpha\right) }}{{\ell^{3}}}+\frac{{{W}_{4}}\,{{\alpha}^{3}}\,\sin{\left( \alpha\right) }}{{\ell^{3}}}&=&0 \end{array}</math>, | |||
vereinfacht und in Matrix-Schreibweise | |||
::<math>\underbrace{\begin{pmatrix}0 & 1 & 0 & 1\\ 1 & 0 & 1 & 0\\ \operatorname{sinh}\left( \alpha\right) & \cosh{\left( \alpha\right) } & -\sin{\left( \alpha\right) } & -\cos{\left( \alpha\right) }\\ \cosh{\left( \alpha\right) } & \operatorname{sinh}\left( \alpha\right) & -\cos{\left( \alpha\right) } & +\sin{\left( \alpha\right) }\end{pmatrix}}_{\displaystyle \underline{\underline{D}}(\kappa)} \cdot \begin{pmatrix}W_1\\ W_2\\ W_3\\W_4\end{pmatrix} = \underline{0}</math>. | |||
Für dieses lineare, homogenen Gleichungen gibt es nur dann nicht-triviale Lösungen, wenn die Matrix einen Rangabfall >= 1 hat, also | |||
::<math>\det(\underline{\underline{D}}(\alpha))\stackrel{!}{=}0</math>. | |||
Wir finden die charakteristische Gleichung | |||
::<math>-{{{\sinh}\left( \alpha\right) }^{2}}+{{\sin{\left( \alpha\right) }}^{2}}+{{\cosh{\left( \alpha\right) }}^{2}}+2\cos{\left( \alpha\right) }\,\cosh{\left( \alpha\right) }+{{\cos{\left( \alpha\right) }}^{2}}\stackrel{!}{=}0</math>. | |||
Beim Plotten der Funktion sehen wir bereits, dass es mehr als eine Nullstelle gibt, hier bei ''α≈+/- 2'' und ''α≈+/- 5.'' [[Datei:UEBE-23.png|mini|Charakteristische Gleichung]]Die charakteristische Gleichung können wir umformen zu | |||
<math>\cos(\alpha)\cdot\cosh(\alpha)+1\stackrel{!}{=}0</math> | |||
und beide Anteile auftragen. So wird klar, dass die beiden Funktionen sich wegen der Periodizität der cos-Funktion unendlich oft schneiden - es also unendlich viele Nullstellen gibt: | |||
<table class="wikitable" style="background-color:white;"> | |||
<tr> | |||
<td>[[Datei:UEBE-21.png|mini|Nullstellensuche (Ausschnitt)|alternativtext=|ohne]]</td> | |||
<td>[[Datei:UEBE-24.png|mini|Nullstellensuche|alternativtext=|ohne]]</td> | |||
</tr> | |||
</table> | |||
Analytisch finden wir keine Lösungen dieser charakteristischen Gleichung - wir müssen sie numerisch bestimmen – hier mit der Maxima-Funktion "find_root". Die ersten (positiven) Lösungen sind | |||
::<math>\begin{array}{l}\alpha_1=1.875104068711961,\\ \alpha_2=4.694091132974175,\\ \alpha_3=7.854757438237613,\\ \alpha_4=10.99554073487547,\\\alpha_5=14.13716839104647,\\\alpha_6=17.27875953208824\end{array}</math>. | |||
Sie zu finden ist einfach, weil die ''α<sub>i</sub>'' für ''i>1'' ungefähr ''π'' auseinander liegen - da können wir keine Nullstelle verpassen. | |||
In diesen ''α''<sub>i</sub> stecken über <math>\omega_{0,i} = 2\,\pi/T_i</math> auch der Periodendauern, z.B. für die erste Mode | |||
::<math>\displaystyle T_1 = 0.5688\ldots \pi \ell^2 \sqrt{\frac{\varrho\,A}{E\,I}}</math>. | |||
Wie bei einem normalen [[Werkzeuge/Lösungsbausteine der Mathematik/Eigenwertprobleme|Eigenwertproblem]] berechnen wir nun die Eigenvektoren ''<u>W</u>'' aus der Beziehung | |||
::<math>\underline{\underline{D}}(\alpha_i)\cdot \underline{W} = \underline{0}</math>. | |||
Aus unendlich vielen Lösungen ''α<sub>i</sub>'' folgen nun also auch unendlich viele ''W<sub>j</sub>'', die wir zu | |||
::<math>\left(\begin{array}{c}W_1\\W_2\\W_3\\W_4\end{array}\right)_j = C_j\cdot \left(\begin{array}{r}\gamma_j\\-1\\-\gamma_j\\1\end{array}\right) \text{ mit } \displaystyle \gamma_j = \frac{\cosh{\left( \alpha_j\right) }+\cos{\left( \alpha_j\right) }}{\sinh\left( \alpha_j\right) +\sin{\left( \alpha_j\right) }}</math> | |||
bestimmen. Die homogene Lösung der Bewegungsgleichung ist also | |||
< | ::<math>\displaystyle w_h(x,t) = \sum_{j=1}^{\infty} C_j \cdot \underbrace{\left( \gamma_i,-1,-\gamma_j,1\right) \cdot \left(\begin{array}{r} \sinh(\alpha_j\,\xi)\\\cosh(\alpha_j\,\xi)\\\sin(\alpha_j\,\xi)\\\cos(\alpha_j\,\xi)\end{array}\right)}_{\displaystyle =: \phi_j(\xi)}\cdot e^{\displaystyle \omega_{0,j}\,t} \text{ mit } \xi = \frac{x}{\ell}</math>. | ||
Denken Sie daran: die Eigenkreisfrequenz ''ω<sub>0j</sub>'' ist dabei wieder eine Funktion von ''α<sub>i</sub>'' - siehe oben. Die ''C<sub>i</sub>'' sind wieder Konstanten, die wir brauchen, um die Lösung an die Anfangsbedingungen anzupassen. Zunächst schauen wir uns die Lösung jeweils zu einem ''α<sub>i</sub>'' an. Diese Funktionen heißen Modalformen ''ϕ'' und deren Schwingungen können wir plotten: | |||
<table class="wikitable" style="background-color:white;"> | |||
<tr> | |||
<th>Mode</th><th>Modalform ϕ<sub>j</sub></th> | |||
<th>Mode</th><th>Modalform ϕ<sub>j</sub></th></tr> | |||
<tr> | |||
<td>'''#1'''<br /><math>\displaystyle \omega_{0,1} = 1\cdot \frac{2 \pi}{T}</math></td><td>[[Datei:UEBE-mode-1-animated.gif|rahmenlos]]</td> | |||
<td>'''#2'''<br /><math>\displaystyle \omega_{0,2} = 6.27\cdot \frac{2 \pi}{T}</math></td><td>[[Datei:UEBE-mode-2-animated.gif|rahmenlos]]</td> | |||
</tr> | |||
<tr> | |||
<td>'''#3'''<br /><math>\displaystyle \omega_{0,3} = 17.5\cdot \frac{2 \pi}{T}</math></td><td>[[Datei:UEBE-mode-3-animated.gif|rahmenlos]]</td> | |||
<td>'''#4'''<br /><math>\displaystyle \omega_{0,4} = 34.4\cdot \frac{2 \pi}{T}</math></td><td>[[Datei:UEBE-mode-4-animated.gif|rahmenlos]]</td> | |||
</tr> | |||
<tr> | |||
<td>'''#5'''<br /><math>\displaystyle \omega_{0,5} = 56.8\cdot \frac{2 \pi}{T}</math></td><td>[[Datei:UEBE-mode-5-animated.gif|rahmenlos]]</td> | |||
<td>'''#6'''<br /><math>\displaystyle \omega_{0,6} = 84.9\cdot \frac{2 \pi}{T}</math></td><td>[[Datei:UEBE-mode-6-animated.gif|rahmenlos]]</td> | |||
</tr> | |||
</table> | |||
[[Datei:UEBE-31.png|mini|Modalformen]]Diese Moden ''ϕ<sub>j</sub>'' können wir auch einzeln übereinander darstellen: | |||
| | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /***************************************************************************/ | ||
/* h o m o g e n e o u s s o l u t i o n */ | |||
/***************************************************************************/ | |||
ansatz: w(x,t) = W[i] * %e^(kappa*x) * %e^(%i*omega[0]*t); | |||
heom : subst(ansatz,subst([g=0],eom)); | |||
heom : ratsimp(subst(ansatz,ev(heom,nouns)/w(x,t))); | |||
sol[1] : subst(abbrev,solve(heom,kappa)); | |||
/* ansatz: w(x,t) = sum(subst(sol[1][i],subst(ansatz,w(x,t))),i,1,length(sol[1])); */ | |||
/* this is possible - but results in complex W[i] - too demanding */ | |||
ansatz : w(x,t) = subst(sol[1][1], W[1]*%e^(kappa*x)*%e^(%i*omega[0]*t)) | |||
+subst(sol[1][2], W[2]*%e^(kappa*x)*%e^(%i*omega[0]*t)) | |||
+subst(sol[1][3], W[3]*%e^(kappa*x)*%e^(%i*omega[0]*t)) | |||
+subst(sol[1][4], W[4]*%e^(kappa*x)*%e^(%i*omega[0]*t)); | |||
/* .. but we can rephrase w(x,t) with | |||
https://de.wikipedia.org/wiki/Sinus_hyperbolicus_und_Kosinus_hyperbolicus | |||
to have only real-values W[i]: */ | |||
ansatz : w(x,t) =( W[1]*sinh(kappa*x) | |||
+W[2]*cosh(kappa*x) | |||
+W[3]*sin (kappa*x) | |||
+W[4]*cos (kappa*x))*%e^(%i*omega[0]*t); | |||
/* test:subst(ansatz,heom);ratsimp(ev(%,nouns));subst([x=xi*l[0]],%);subst(abbrev[1],%);*/ | |||
/* boundary conditions */ | |||
BouCon : [subst([x= 0 ], subst(ansatz,w(x,t)) )/%e^(%i*omega[0]*t)=0, | |||
subst([x= 0 ], diff(subst(ansatz,w(x,t)),x ))/%e^(%i*omega[0]*t)=0, | |||
subst([x=l[0]], diff(subst(ansatz,w(x,t)),x,2))/%e^(%i*omega[0]*t)=0, | |||
subst([x=l[0]], diff(subst(ansatz,w(x,t)),x,3))/%e^(%i*omega[0]*t)=0]; | |||
D : submatrix(augcoefmatrix(expand(BouCon),makelist(W[i],i,1,4)),5); | |||
/* what happens to the six alpha=0 ???? */ | |||
D : diag_matrix (1, 1/kappa, 1/kappa^2,1/kappa^3).subst(abbrev,D); | |||
D : subst(solve(sol[1][4],kappa),D); | |||
CharEqua : expand(determinant(D))=0; | |||
CharEqua : ratsimp(subst([sin(alpha)^2=1-cos(alpha)^2,sinh(alpha)^2=cosh(alpha)^2-1], CharEqua/2)); | |||
/* numerically find zeros for omega[0] (alpha) */ | |||
plot2d(lhs(CharEqua),[alpha,-6,6], [y,-6,6], [ylabel,"lhs(CharEqua)→"], [xlabel,"α→"], [style, [lines,3]])$ | |||
plot2d([cos(alpha),-1/cosh(alpha)],[alpha,0,60], [ylabel,"f(α)→"], [xlabel,"α→"], [style, [lines,3]])$ | |||
guessed: [2,5,8,11,14,17]; | |||
zeros : makelist(alpha = find_root(CharEqua/alpha^6, alpha, guessed[i]-1/2, guessed[i]+1/2),i,1,length(guessed)); | |||
sol[2] : makelist(omega[0] = subst(zeros[i],subst(abbrev[3],sqrt(omega[0]))^2),i,1,length(zeros)); | |||
params : append(params, [T[ref] = subst(zeros[1],subst(abbrev,2*%pi/omega[0]))]); | |||
/* use upper triangular matrix instead of D */ | |||
[P,L,U] : get_lu_factors(lu_factor(D))$ | |||
/* get eigenvectors */ | |||
EigVec : subst(solve(makelist(sum(U[j][i]*W[i],i,1,4)=0,j,1,3),[W[1],W[2],W[3]])[1], | |||
matrix([W[1]],[W[2]],[W[3]],[W[4]])); | |||
EigVec : subst(abbrev,subst([W[4]=1],EigVec)); | |||
Gammas : makelist(gamma = subst(zeros[i],subst(abbrev[2],gamma)),i,1,length(zeros)); | |||
modeshape : subst(abbrev[2],subst([x=xi*l[0]],subst(sol[1][4],subst(makelist(W[i]=EigVec[i][1],i,1,4), | |||
subst(params,subst([t=T[ref]*tau],subst(abbrev,subst(ansatz,w(x,t))))))))); | |||
modes : makelist(subst(zeros[i],modeshape),i,1,length(zeros)); | |||
/* plot mode snapshots for animation -> convert with imageMagick */ | |||
fpprintprec: 3$ | |||
titles : makelist(simplode(["ω/ω1 = ",subst(sol[2][1],subst(sol[2][i],omega[0])/omega[0])]),i,1,6); | |||
NSteps : 19$ | |||
for mode: 1 thru 6 do | |||
for j:0 thru NSteps do | |||
(tstep : simplode([if j<10 then "0" else "",j]), | |||
plot2d(subst([tau=j/(NSteps+1)],subst([tau=0],modes[mode])*sin(2*%pi*tau)),[xi,0,1], | |||
[title, titles[mode]], [legend, simplode(["t/T=",float(j/NSteps+0.01)])], | |||
[style, [lines,3,1]], [xlabel, "ξ →"], [ylabel, "← w "], | |||
[png_file,simplode([workdir,"mode-",mode,"-step-",tstep,".png"])], | |||
[gnuplot_preamble, "set yrange [2.1:-2.1] reverse"]))$ | |||
/* plot all modeshapes (1...6)*/ | |||
legends : append([legend],makelist(simplode(["mode ",i]), i,1,length(zeros))); | |||
plot2d(subst([tau=0],modes), [xi,0,1], legends, | |||
[xlabel, "ξ →"], [ylabel, "← w "], | |||
[gnuplot_preamble, "set yrange [2.1:-2.1] reverse"])$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Adapt to Initial Condition | {{MyCodeBlock|title=Adapt to Initial Condition | ||
|text= | |text= | ||
Zum Zeitpunkt ''t=0'' soll | |||
::<math>\underbrace{w_h(x,0)}_{\displaystyle = \sum_{j=1}^{\infty} C_j\cdot \phi_{j}(x)} + w_p(x) = 0</math> | |||
gelten. Das kriegen wir hin, indem wir die (unendlich vielen) ''C<sub>i</sub>'' der homogenen Lösung passend wählend. Das klingt komplizierter als es ist - die Mathematik bereitet uns den Weg. | |||
Die Beziehung oben multiplizieren wir dazu mit einer der Modalformen ''ϕ<sub>k</sub>'' und bilden das Integral über die Balken-Lange ''ℓ'', also | |||
::<math>\displaystyle \sum_{j=1}^{\infty} \left( C_j\cdot \int_{0}^{\ell}\phi_{j}(x) \cdot \phi_{k}(x)\;dx \right) + \int_{0}^{\ell} w_p(x)\cdot \phi_{k}(x)\;dx = 0</math> | |||
Wir projizieren also die Modalformen auf sich selbst und auf die partikulare Lösung. Und nutzen aus, dass diese [https://de.wikipedia.org/wiki/Faltung_(Mathematik) Faltungs-Integrale] der Modalformen eine besondere Eigenschaft haben: | |||
::<math>\displaystyle \int_{0}^{\ell} \phi_j \cdot \phi_k \; dx \left\{ \begin{array}{l} =0 \text{ für } j\ne k \\ \ne 0 \text{ für } j = k \end{array} \right.</math> | |||
Man sagt: die Funktionen sind zueinander verallgemeinert orthogonal. Damit berechnen wir | |||
::<math>\begin{array}{l} C_{1}=0.506693895146775,\\C_{2}=0.007150056863941781,\\C_{3}=5.347110562156877\;10^{-4},\\ C_{4}=9.955236981148623\;10^{-5},\\C_{5}=2.833383071646469\;10^{-5},\\C_{6}= 1.038598312000442\;10^{-5}\\ \;\;\;\;\;\vdots\end{array}</math>, | |||
Nur die erste Modalform liefert einen signifikanten Beitrag bei der Anpassung an die Anfangsbedingungen, wir nehmen bei der Auftragung der Gesamtlösung ''w<sub>t</sub>(x,t)'' trotzdem die ersten sechs Modalformen mit: | |||
[[Datei:UEBE-initial-value-solution-animation.gif|mini|Animation: Loslassen des Systems aus der unverformten Rugelage.|ohne]] | |||
In der Animation sehen Sie das Loslassen des Stabes aus der unverformten, geraden Referenzlage für genau eine Periodenlänge ''T<sub>1</sub>'' der ersten Modalform. Allerdings ist die Schwingung, die entsteht, nicht ''T<sub>1</sub>''-periodisch - die anderen Modalformen leisten einen (kleinen) Beitrag, dessen Schwingungsperiode kein Vielfaches der Grundschwingung ist. Das sehen sie an dem kleinen "Ruck" in der Darstellung der Lösung, wenn nach der Dauer ''T<sub>1</sub>'' der Grundschwingung wieder die Anfangslage eingeblendet wird. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /***************************************************************************/ | ||
/* t o t a l ( c o m p o s e d ) s o l u t i o n */ | |||
/***************************************************************************/ | |||
w[h] : sum(C[i]*modes[i],i,1,length(zeros)); | |||
/* adapt to inital condition w[h]+w[p]=0 */ | |||
/* Faltungsintegrale */ | |||
FI : [integrate(expand(subst([tau=0],modeshape^2)),xi,0,1), | |||
integrate(expand(subst([tau=0],modeshape*ratsimp(subst(params,subst(w[p],w(x,t))/w[s])))),xi,0,1)]; | |||
/* coefficients for mode shapes */ | |||
IVs : makelist(C[i] = -subst(zeros[i],FI[2]/FI[1]),i,1,length(zeros)); | |||
w[h] : subst(IVs,realpart(w[h])); | |||
/* produce slides for animation */ | |||
fpprintprec: 3$ | |||
NSteps : 39$ | |||
for j:0 thru NSteps-1 do | |||
(tstep : simplode([if j<10 then "0" else "",j]), | |||
plot2d(subst([tau=j/NSteps],w[h])+ratsimp(subst(params,subst(w[p],w(x,t))/w[s])),[xi,0,1], | |||
[legend, simplode(["t/T=",float(j/NSteps+0.01)])], | |||
[style, [lines,3,1]], [xlabel, "ξ →"], [ylabel, "← w"], | |||
[png_file,simplode([workdir,"initial-value-solution-step-",tstep,".png"])], | |||
[gnuplot_preamble, "set yrange [2.5:-0.5] reverse"]))$ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
{{MyWarning | |||
|title=Timoshenko-Balken | |||
|text=Wieviele Moden man berücksichtigen muss, hängt von vielen praktischen Faktoren - z.B. der modalen Dämpfung - ab. Vergessen sollte man nicht, dass je nach Stab-Länge, der Einfluss der Schubverformung bei den höheren Moden zunimmt. Dann muss man ggf. das Modell wechseln ... | |||
}} | |||
{{MyTip | |||
|title=Saiteninstruente | |||
|text= | |||
Bei Saiteninstrumenten möchte man Biegeschwingungen der Saiten verhindern. Darum sind besonders die Saiten, die eine hohe Massebelegung brauchen, um in niedrigen Frequenzen zu schwingen, besondere Konstruktionen. Dabei wird oft ein Draht um die eigentliche Saite gewickelt. Können Sie aus diesen Untersuchungen erkennen, was das Ziel dieser Konstruktion ist? | |||
}} | |||
<hr /> | <hr /> | ||
'''Links''' | '''Links''' | ||
* | * Schwingungen von Kontinua eines Dehnstabes ([[Gelöste Aufgaben/SKER|SKER]]) | ||
'''Literature''' | '''Literature''' | ||
*... | *... | ||
Aktuelle Version vom 3. April 2021, 19:19 Uhr
Aufgabenstellung
Die Bewegung des Balkens wird durch das Zusammenspiel von elastischen Verformungen und Trägheitskräften bestimmt. Man nennt das "Schwingungen von Kontinua" - diese untersuchen wir hier. Der zentrale Aufgabe besteht in der Berechnung der homogenen Lösung - und der Anpassung der Lösungsanteile an die Anfangsbedingungen.
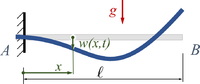
Gesucht ist analytische Lösung für Schwingungen des Euler-Bernoulli-Balkens beim Loslassen aus der enspannten Ruhelage.
Lösung mit Maxima
Header
Für die mathematische Behandlung - insbesondere der Auflösung quadratischer Gleichungen - setzen wir in Maxima voraus, dass
- .
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 16.04.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-01-15 */
/* ref: oscillations of continuous media */
/* description: analytic solutioun for EBB */
/*******************************************************/
/* settings */
workdir: "C:\\Users\\X...X\\plots\\";
/* assumptions */
assume(rho>0, E>0,I>0,A>0,l[0]>0,alpha>0,gamma>0);
/* abbreviations used later .... */
abbrev : [alpha = (sqrt(omega[0])*A^(1/4)*rho^(1/4)*l[0])/(E^(1/4)*I^(1/4)),
gamma = ((cosh(alpha)+cos(alpha)))/(sinh(alpha)+sin(alpha))];
abbrev : append(abbrev, solve(abbrev,[sqrt(omega[0]),cosh(alpha)])[1]);
abbrev : append(abbrev, [abbrev[3]^2,abbrev[3]^3]);
Equations of Motion
In der Gleichgewichtsbeziehung für den Euler-Bernoulli-Balken setzen wir als eingeprägte, äußere Streckenlast q(x,t) die D'Alembert'sche Trägheitskraft und die Gewichtskraft an, also
Die Lösung der linearen, partielle Bewegungsgleichung
setzt sich dann aus zwei Lösungsanteilen, der partikularen Lösung wp und der homogenen Lösung wh, zusammen; wir schreiben
- .
/* equation of motion */
eom: rho*A*diff(w(x,t),t,2) + E*I*diff(w(x,t),x,4) = rho*A*g;
Particular Solution
Die partikulare Lösung wp erfüllt die "rechte Seite" der Bewegungsgleichung, also ϱ A⋅g:
- .
Die rechte Seite ist zeit-unveränderlich - so auch die partikulare Lösung.
Wir integrieren die Bewegungsgleichung vier Mal und erhalten
- .
Die vier Integrationskonstanten Ci müssen wir nun an die Randbedingungen
anpassen, wir erhalten mit dem linearen Gleichungssystem
die partikulare Lösung
- .
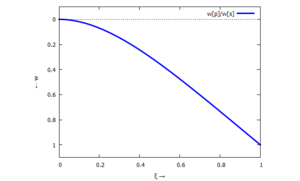
Die maximale Auslenkung - am rechten Rand - nutzen wir als Bezugslänge
Und so sieht wp aus:
/***************************************************************************/
/* p a r t i c u l a r s o l u t i o n */
/***************************************************************************/
peom : subst(['diff(w(x,t),t,2)=0],eom);
w[p] : integrate(integrate(integrate(integrate(peom,x),x),x),x);
w[p] : subst([%c1=C[3],%c2=C[2],%c3=C[1],%c4=C[0]],w[p]);
BouCon : [subst([x= 0 ],subst([ w(x,t) =0], w[p] )),
subst([x= 0 ],subst(['diff(w(x,t),x,1)=0],diff(w[p],x,1))),
subst([x=l[0]],subst(['diff(w(x,t),x,2)=0],diff(w[p],x,2))),
subst([x=l[0]],subst(['diff(w(x,t),x,3)=0],diff(w[p],x,3)))];
w[p] : subst(solve(BouCon,makelist(C[i],i,0,3))[1],w[p]);
w[p] : ratsimp(lhs(w[p]/(E*I)) = subst([x=l[0]*xi], rhs(w[p])/(E*I)));
params: [w[s] = subst([xi=1],subst(w[p],w(x,t))), omega[0]=2*%pi/T];
plot2d(ratsimp(subst(params,subst(w[p],w(x,t))/w[s])),[xi,0,1],
[legend, "w[p]/w[s]"],
[style, [lines,3,1]], [xlabel, "ξ →"], [ylabel, "← w"],
[gnuplot_preamble, "set yrange [1.1:-0.1] reverse"])$
Homogeneous Solution
Die homogene Bewegungsgleichung
lässt Lösungen vom Typ
zu. Wir bekommen zu jedem ω0 vier κ
- ,
also
Die komplexen Exponenten deuten schon darauf hin: im Allgemeinen sind die Koeffizienten Wi ebenfalls komplex. Für dieses Beispiel macht es deshalb viel Sinn, diese allgemeine Lösung der homogenen Differentialgleichung etwas anders hinzuschreiben. Wir nutzen dafür:
- die Hyperbelfunktionen
- die Euler'sche Formel
Dann lautet die allgemeine Lösung
- ,
bei der wir davon ausgehen dürfen, dass alle Wi reellwertig sind.
Wie bei der partikularen Lösung wp sind es die vier Integrationskonstanten Wi, die wir nun an die Randbedingungen
anpassen müssen. Wir erhalten das lineare Gleichungssystem
- ,
vereinfacht und in Matrix-Schreibweise
- .
Für dieses lineare, homogenen Gleichungen gibt es nur dann nicht-triviale Lösungen, wenn die Matrix einen Rangabfall >= 1 hat, also
- .
Wir finden die charakteristische Gleichung
- .
Beim Plotten der Funktion sehen wir bereits, dass es mehr als eine Nullstelle gibt, hier bei α≈+/- 2 und α≈+/- 5.
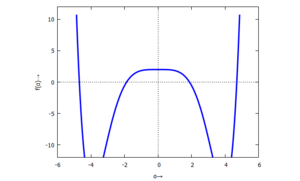
Die charakteristische Gleichung können wir umformen zu
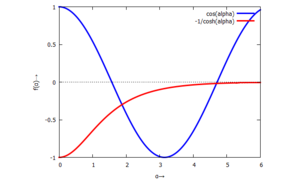
und beide Anteile auftragen. So wird klar, dass die beiden Funktionen sich wegen der Periodizität der cos-Funktion unendlich oft schneiden - es also unendlich viele Nullstellen gibt:
 |
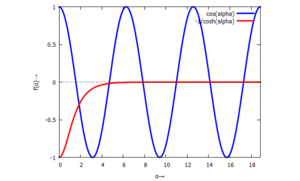 |
Analytisch finden wir keine Lösungen dieser charakteristischen Gleichung - wir müssen sie numerisch bestimmen – hier mit der Maxima-Funktion "find_root". Die ersten (positiven) Lösungen sind
- .
Sie zu finden ist einfach, weil die αi für i>1 ungefähr π auseinander liegen - da können wir keine Nullstelle verpassen.
In diesen αi stecken über auch der Periodendauern, z.B. für die erste Mode
- .
Wie bei einem normalen Eigenwertproblem berechnen wir nun die Eigenvektoren W aus der Beziehung
- .
Aus unendlich vielen Lösungen αi folgen nun also auch unendlich viele Wj, die wir zu
bestimmen. Die homogene Lösung der Bewegungsgleichung ist also
- .
Denken Sie daran: die Eigenkreisfrequenz ω0j ist dabei wieder eine Funktion von αi - siehe oben. Die Ci sind wieder Konstanten, die wir brauchen, um die Lösung an die Anfangsbedingungen anzupassen. Zunächst schauen wir uns die Lösung jeweils zu einem αi an. Diese Funktionen heißen Modalformen ϕ und deren Schwingungen können wir plotten:
| Mode | Modalform ϕj | Mode | Modalform ϕj |
|---|---|---|---|
| #1 | 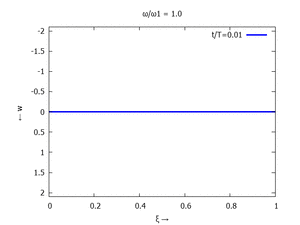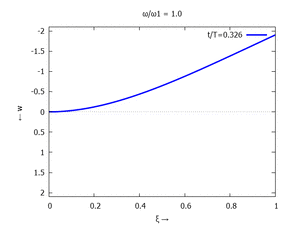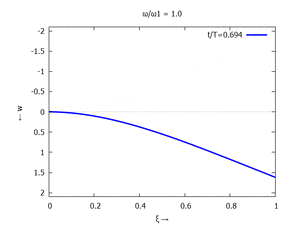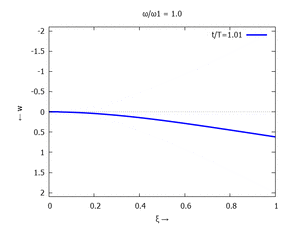 |
#2 | 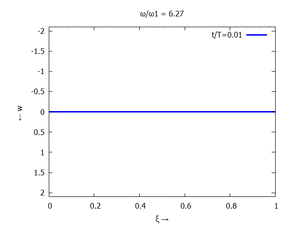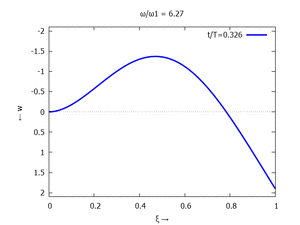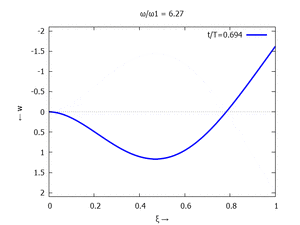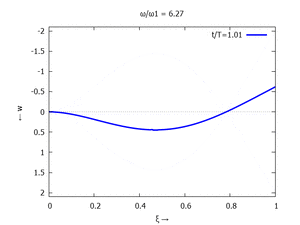 |
| #3 | 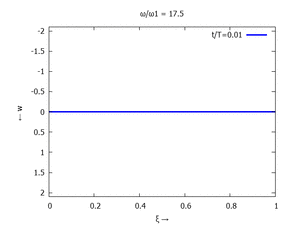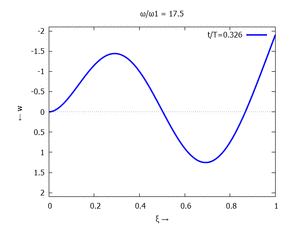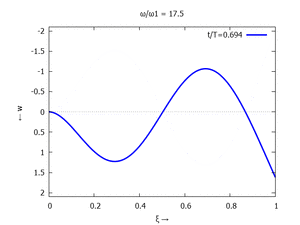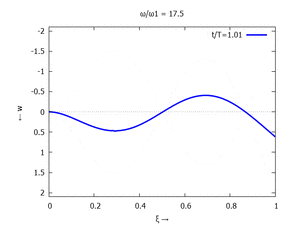 |
#4 | 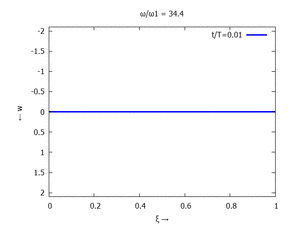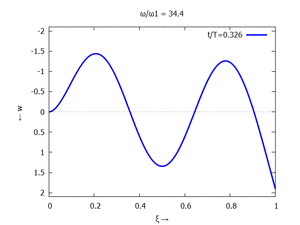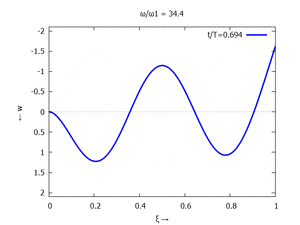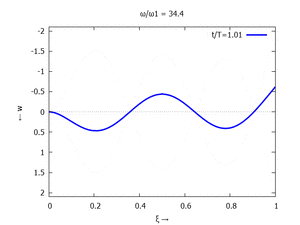 |
| #5 | 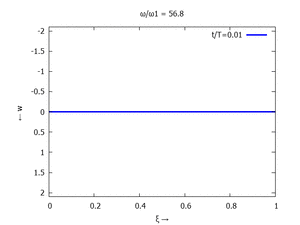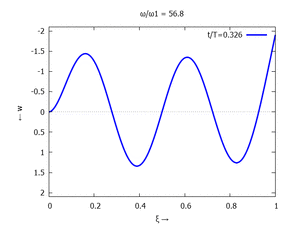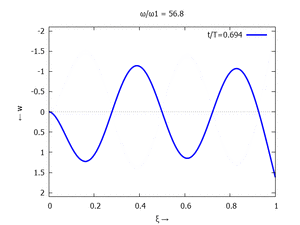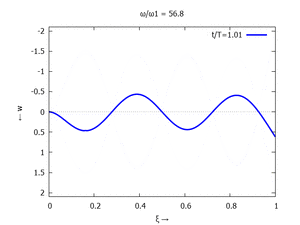 |
#6 | 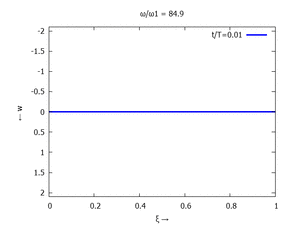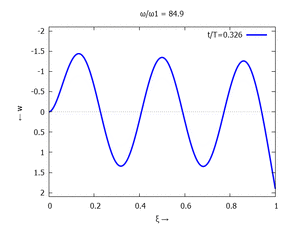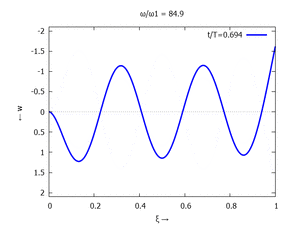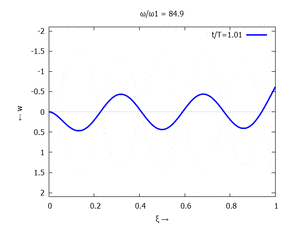 |
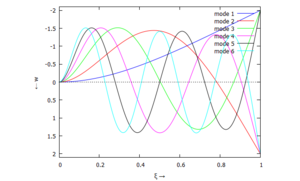
Diese Moden ϕj können wir auch einzeln übereinander darstellen:
/***************************************************************************/
/* h o m o g e n e o u s s o l u t i o n */
/***************************************************************************/
ansatz: w(x,t) = W[i] * %e^(kappa*x) * %e^(%i*omega[0]*t);
heom : subst(ansatz,subst([g=0],eom));
heom : ratsimp(subst(ansatz,ev(heom,nouns)/w(x,t)));
sol[1] : subst(abbrev,solve(heom,kappa));
/* ansatz: w(x,t) = sum(subst(sol[1][i],subst(ansatz,w(x,t))),i,1,length(sol[1])); */
/* this is possible - but results in complex W[i] - too demanding */
ansatz : w(x,t) = subst(sol[1][1], W[1]*%e^(kappa*x)*%e^(%i*omega[0]*t))
+subst(sol[1][2], W[2]*%e^(kappa*x)*%e^(%i*omega[0]*t))
+subst(sol[1][3], W[3]*%e^(kappa*x)*%e^(%i*omega[0]*t))
+subst(sol[1][4], W[4]*%e^(kappa*x)*%e^(%i*omega[0]*t));
/* .. but we can rephrase w(x,t) with
https://de.wikipedia.org/wiki/Sinus_hyperbolicus_und_Kosinus_hyperbolicus
to have only real-values W[i]: */
ansatz : w(x,t) =( W[1]*sinh(kappa*x)
+W[2]*cosh(kappa*x)
+W[3]*sin (kappa*x)
+W[4]*cos (kappa*x))*%e^(%i*omega[0]*t);
/* test:subst(ansatz,heom);ratsimp(ev(%,nouns));subst([x=xi*l[0]],%);subst(abbrev[1],%);*/
/* boundary conditions */
BouCon : [subst([x= 0 ], subst(ansatz,w(x,t)) )/%e^(%i*omega[0]*t)=0,
subst([x= 0 ], diff(subst(ansatz,w(x,t)),x ))/%e^(%i*omega[0]*t)=0,
subst([x=l[0]], diff(subst(ansatz,w(x,t)),x,2))/%e^(%i*omega[0]*t)=0,
subst([x=l[0]], diff(subst(ansatz,w(x,t)),x,3))/%e^(%i*omega[0]*t)=0];
D : submatrix(augcoefmatrix(expand(BouCon),makelist(W[i],i,1,4)),5);
/* what happens to the six alpha=0 ???? */
D : diag_matrix (1, 1/kappa, 1/kappa^2,1/kappa^3).subst(abbrev,D);
D : subst(solve(sol[1][4],kappa),D);
CharEqua : expand(determinant(D))=0;
CharEqua : ratsimp(subst([sin(alpha)^2=1-cos(alpha)^2,sinh(alpha)^2=cosh(alpha)^2-1], CharEqua/2));
/* numerically find zeros for omega[0] (alpha) */
plot2d(lhs(CharEqua),[alpha,-6,6], [y,-6,6], [ylabel,"lhs(CharEqua)→"], [xlabel,"α→"], [style, [lines,3]])$
plot2d([cos(alpha),-1/cosh(alpha)],[alpha,0,60], [ylabel,"f(α)→"], [xlabel,"α→"], [style, [lines,3]])$
guessed: [2,5,8,11,14,17];
zeros : makelist(alpha = find_root(CharEqua/alpha^6, alpha, guessed[i]-1/2, guessed[i]+1/2),i,1,length(guessed));
sol[2] : makelist(omega[0] = subst(zeros[i],subst(abbrev[3],sqrt(omega[0]))^2),i,1,length(zeros));
params : append(params, [T[ref] = subst(zeros[1],subst(abbrev,2*%pi/omega[0]))]);
/* use upper triangular matrix instead of D */
[P,L,U] : get_lu_factors(lu_factor(D))$
/* get eigenvectors */
EigVec : subst(solve(makelist(sum(U[j][i]*W[i],i,1,4)=0,j,1,3),[W[1],W[2],W[3]])[1],
matrix([W[1]],[W[2]],[W[3]],[W[4]]));
EigVec : subst(abbrev,subst([W[4]=1],EigVec));
Gammas : makelist(gamma = subst(zeros[i],subst(abbrev[2],gamma)),i,1,length(zeros));
modeshape : subst(abbrev[2],subst([x=xi*l[0]],subst(sol[1][4],subst(makelist(W[i]=EigVec[i][1],i,1,4),
subst(params,subst([t=T[ref]*tau],subst(abbrev,subst(ansatz,w(x,t)))))))));
modes : makelist(subst(zeros[i],modeshape),i,1,length(zeros));
/* plot mode snapshots for animation -> convert with imageMagick */
fpprintprec: 3$
titles : makelist(simplode(["ω/ω1 = ",subst(sol[2][1],subst(sol[2][i],omega[0])/omega[0])]),i,1,6);
NSteps : 19$
for mode: 1 thru 6 do
for j:0 thru NSteps do
(tstep : simplode([if j<10 then "0" else "",j]),
plot2d(subst([tau=j/(NSteps+1)],subst([tau=0],modes[mode])*sin(2*%pi*tau)),[xi,0,1],
[title, titles[mode]], [legend, simplode(["t/T=",float(j/NSteps+0.01)])],
[style, [lines,3,1]], [xlabel, "ξ →"], [ylabel, "← w "],
[png_file,simplode([workdir,"mode-",mode,"-step-",tstep,".png"])],
[gnuplot_preamble, "set yrange [2.1:-2.1] reverse"]))$
/* plot all modeshapes (1...6)*/
legends : append([legend],makelist(simplode(["mode ",i]), i,1,length(zeros)));
plot2d(subst([tau=0],modes), [xi,0,1], legends,
[xlabel, "ξ →"], [ylabel, "← w "],
[gnuplot_preamble, "set yrange [2.1:-2.1] reverse"])$
Adapt to Initial Condition
Zum Zeitpunkt t=0 soll
gelten. Das kriegen wir hin, indem wir die (unendlich vielen) Ci der homogenen Lösung passend wählend. Das klingt komplizierter als es ist - die Mathematik bereitet uns den Weg.
Die Beziehung oben multiplizieren wir dazu mit einer der Modalformen ϕk und bilden das Integral über die Balken-Lange ℓ, also
Wir projizieren also die Modalformen auf sich selbst und auf die partikulare Lösung. Und nutzen aus, dass diese Faltungs-Integrale der Modalformen eine besondere Eigenschaft haben:
Man sagt: die Funktionen sind zueinander verallgemeinert orthogonal. Damit berechnen wir
- ,
Nur die erste Modalform liefert einen signifikanten Beitrag bei der Anpassung an die Anfangsbedingungen, wir nehmen bei der Auftragung der Gesamtlösung wt(x,t) trotzdem die ersten sechs Modalformen mit:
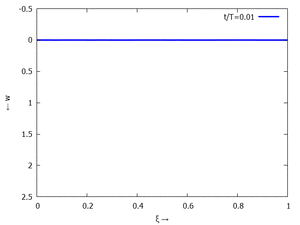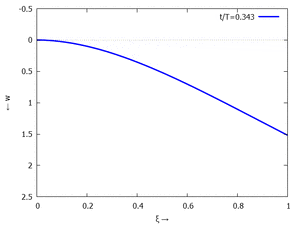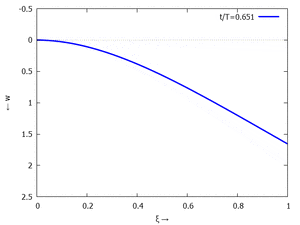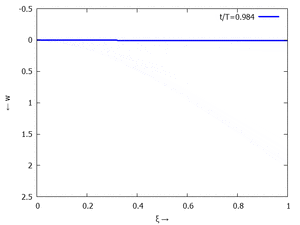
In der Animation sehen Sie das Loslassen des Stabes aus der unverformten, geraden Referenzlage für genau eine Periodenlänge T1 der ersten Modalform. Allerdings ist die Schwingung, die entsteht, nicht T1-periodisch - die anderen Modalformen leisten einen (kleinen) Beitrag, dessen Schwingungsperiode kein Vielfaches der Grundschwingung ist. Das sehen sie an dem kleinen "Ruck" in der Darstellung der Lösung, wenn nach der Dauer T1 der Grundschwingung wieder die Anfangslage eingeblendet wird.
/***************************************************************************/
/* t o t a l ( c o m p o s e d ) s o l u t i o n */
/***************************************************************************/
w[h] : sum(C[i]*modes[i],i,1,length(zeros));
/* adapt to inital condition w[h]+w[p]=0 */
/* Faltungsintegrale */
FI : [integrate(expand(subst([tau=0],modeshape^2)),xi,0,1),
integrate(expand(subst([tau=0],modeshape*ratsimp(subst(params,subst(w[p],w(x,t))/w[s])))),xi,0,1)];
/* coefficients for mode shapes */
IVs : makelist(C[i] = -subst(zeros[i],FI[2]/FI[1]),i,1,length(zeros));
w[h] : subst(IVs,realpart(w[h]));
/* produce slides for animation */
fpprintprec: 3$
NSteps : 39$
for j:0 thru NSteps-1 do
(tstep : simplode([if j<10 then "0" else "",j]),
plot2d(subst([tau=j/NSteps],w[h])+ratsimp(subst(params,subst(w[p],w(x,t))/w[s])),[xi,0,1],
[legend, simplode(["t/T=",float(j/NSteps+0.01)])],
[style, [lines,3,1]], [xlabel, "ξ →"], [ylabel, "← w"],
[png_file,simplode([workdir,"initial-value-solution-step-",tstep,".png"])],
[gnuplot_preamble, "set yrange [2.5:-0.5] reverse"]))$
| 🧨 Timoshenko-Balken: |
| Wieviele Moden man berücksichtigen muss, hängt von vielen praktischen Faktoren - z.B. der modalen Dämpfung - ab. Vergessen sollte man nicht, dass je nach Stab-Länge, der Einfluss der Schubverformung bei den höheren Moden zunimmt. Dann muss man ggf. das Modell wechseln ... |
| ✔ Saiteninstruente: |
| Bei Saiteninstrumenten möchte man Biegeschwingungen der Saiten verhindern. Darum sind besonders die Saiten, die eine hohe Massebelegung brauchen, um in niedrigen Frequenzen zu schwingen, besondere Konstruktionen. Dabei wird oft ein Draht um die eigentliche Saite gewickelt. Können Sie aus diesen Untersuchungen erkennen, was das Ziel dieser Konstruktion ist? |
Links
- Schwingungen von Kontinua eines Dehnstabes (SKER)
Literature
- ...