Gelöste Aufgaben/PvV2: Unterschied zwischen den Versionen

Aus numpedia
Zur Navigation springen Zur Suche springen
VisuellWikitext
Keine Bearbeitungszusammenfassung
Keine Bearbeitungszusammenfassung
 
(3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 17: Zeile 17:


== Lösung mit Maxima ==
== Lösung mit Maxima ==
==tmp==


<!-------------------------------------------------------------------------------->
<!-------------------------------------------------------------------------------->
{{MyCodeBlock|title=Title
{{MyCodeBlock|title=Lageplan
|text=Text
|text=[[Datei:PvV2-11.png|mini|Koordinaten|alternativtext=|208x208px]]Hier ist die Leiter mit der Koordinate ''u<sub>1</sub>'' von Punkt ''B'' gezeichnet. Bei der Variation um ''δu'' wandert der Angriffspunktspunkt ''B'' der Kraft ''F'' also in horizontaler Richtung.
|code=
|code=
<syntaxhighlight lang="lisp" line start=1>
<syntaxhighlight lang="lisp" line start=1>
1+1
/*******************************************************/
</syntaxhighlight>
/* MAXIMA script                                       */
}}
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2017-10-08                            */
/* ref: TM-C, PvV mit elastischen Körpern             */
/* description: finds the displacement u employing PvV */
/*******************************************************/
 
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δΠ", alphabetic);
declare("Δl", alphabetic);
declare("δl", alphabetic);
declare("δu", alphabetic);
declare("δη", alphabetic);


==tmp==
assume(EA > 0, l[0]>0, h[0]>0, u[0]>0);
[[Datei:PvV2-11.png|mini|Koordinaten|alternativtext=|208x208px]]Hier ist die Leiter mit der Koordinate ''u<sub>1</sub>'' von Punkt ''B'' gezeichnet. Bei der Variation um ''δu'' wandert der Angriffspunktspunkt ''B'' der Kraft ''F'' also in horizontaler Richtung.<!-------------------------------------------------------------------------------->
/* parameter */
 
params: [h[0]=2*u[0]];
 
{{MyCodeBlock|title=Lageplan
|text=Text
|code=
<syntaxhighlight lang="lisp" line start=1>
1+1
</syntaxhighlight>
</syntaxhighlight>
}}
}}


==tmp==
<!-------------------------------------------------------------------------------->
 
{{MyCodeBlock|title=Kinematik
|text=
Über den Satz des Pythagoras bekommen wir einen Zusammenhang zwischen der Verschiebung ''u<sub>1</sub>'' und der Stablängung ''Δℓ'':
Über den Satz des Pythagoras bekommen wir einen Zusammenhang zwischen der Verschiebung ''u<sub>1</sub>'' und der Stablängung ''Δℓ'':


<math>{{\left( {{\ell}_{0}}+\mathit{\Delta \ell}\right) }^{2}}={{u}_{1}^{2}}+{{h}_{0}^{2}} \text{ also } \mathit{\Delta \ell}(u_1)=\sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}-{{\ell}_{0}}</math>
::<math>{{\left( {{\ell}_{0}}+\mathit{\Delta \ell}\right) }^{2}}={{u}_{1}^{2}}+{{h}_{0}^{2}} \text{ also } \mathit{\Delta \ell}(u_1)=\sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}-{{\ell}_{0}}</math>


Für die Variation ''δℓ'' von ''Δℓ'' führen wir die Hilfsgröße ''ε'' als Koeffizient von ''δu'' ein. Da die virtuelle Verrückung "differentiell klein" sein darf, nehmen wir nur das lineare Glied bzgl. ''δu und'' bekommen mit
Für die Variation ''δℓ'' von ''Δℓ'' führen wir die Hilfsgröße ''ε'' als Koeffizient von ''δu'' ein. Da die virtuelle Verrückung "differentiell klein" sein darf, nehmen wir nur das lineare Glied bzgl. ''δu und'' bekommen mit


<math>\delta\,\ell = \displaystyle \frac{d\,\Delta \ell (u_1+\epsilon\cdot \delta u)}{d\,\epsilon}|_{\epsilon=0}</math>
::<math>\delta\,\ell = \displaystyle \frac{d\,\Delta \ell (u_1+\epsilon\cdot \delta u)}{d\,\epsilon}|_{\epsilon=0}</math>


den Ausdruck
den Ausdruck


<math>\mathit{\delta \ell}=\displaystyle \frac{{{u}_{1}}\cdot \mathit{\delta u}}{\sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}}</math>
::<math>\mathit{\delta \ell}=\displaystyle \frac{{{u}_{1}}\cdot \mathit{\delta u}}{\sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}}</math>.


.
Der Zusammenhang ist nichtlinear! Das ist anschaulich klar - liefert hier jedoch komplizierte Formeln ....
 
Der Zusammenhang ist nichtlinear! Das ist anschaulich klar - liefert hier jedoch komplizierte Formeln ....<!-------------------------------------------------------------------------------->
 
{{MyCodeBlock|title=Kinematik
|text=Text
|code=
|code=
<syntaxhighlight lang="lisp" line start=1>
<syntaxhighlight lang="lisp" line start=1>
1+1
/* Kinematik: */
kinematics: (l[0]+Δl)^2 = h[0]^2+u[1]^2;
ref: solve(l[0]^2 = h[0]^2+u[0]^2,l[0])[2];
/* displacemant and variation */
disp: solve(kinematics,Δl)[2];
disp: [disp, δl=subst(0,epsilon,
        diff(subst([u[1] = u[1]+epsilon*δu],subst(disp,Δl)),
                                                    epsilon))];
</syntaxhighlight>
</syntaxhighlight>
}}
}}


==tmp==
<!-------------------------------------------------------------------------------->
 
{{MyCodeBlock|title=Gleichgewicht
|text=
In das Gleichgewicht gehen alle Arbeiten am System ein.  
In das Gleichgewicht gehen alle Arbeiten am System ein.  


Im Unterschied zu einem Kräftegleichgewicht fallen hier alle Lager-Reaktionskräfte herus: in A und B verschwindet nämlich das Skalarprodukt des virtuellen Verschiebungsvektors mit den Normalkräften auf die Wände - sie stehen senkrecht aufeinander. Im Vergleich zu PvV1 müssen wir allerdings die virtuelle Formänderungsenergie ''δΠ'' berücksichtigen:
Im Unterschied zu einem Kräftegleichgewicht fallen hier alle Lager-Reaktionskräfte herus: in A und B verschwindet nämlich das Skalarprodukt des virtuellen Verschiebungsvektors mit den Normalkräften auf die Wände - sie stehen senkrecht aufeinander. Im Vergleich zu PvV1 müssen wir allerdings die virtuelle Formänderungsenergie ''δΠ'' berücksichtigen:


<math>\begin{array}{rl}\delta W &= \delta W^a -\delta\Pi \\&= -F\cdot \delta u - \displaystyle \frac{EA}{l_0}\cdot\Delta \ell\cdot \delta \ell \\ &\stackrel{!}{=}0 \end{array}</math><!-------------------------------------------------------------------------------->
::<math>\begin{array}{rl}\delta W &= \delta W^a -\delta\Pi \\&= -F\cdot \delta u - \displaystyle \frac{EA}{\ell_0}\cdot\Delta \ell\cdot \delta \ell \\ &\stackrel{!}{=}0 \end{array}</math>
 
{{MyCodeBlock|title=Gleichgewicht
|text=Text
|code=
|code=
<syntaxhighlight lang="lisp" line start=1>
<syntaxhighlight lang="lisp" line start=1>
1+1
/* equilibrium condition */
PvV: [δW=δW^a-δΠ,
      δW^a = -F*δu,
      δΠ = EA/l[0]*Δl*δl];
</syntaxhighlight>
</syntaxhighlight>
}}
}}


==tmp==
<!-------------------------------------------------------------------------------->
===Gleichungen und Unbekannte===


Mit der Gleichung oben haben wir genau eine Gleichung für ''F'' - das passt!.
Mit der Gleichung oben haben wir genau eine Gleichung für ''F'' - das passt!.
Zeile 89: Zeile 99:
Allerdings haben wir zwei Koordinaten ''Δℓ'' und ''u<sub>1</sub>'' sowie deren Variationen. Die Forderung an die virtuellen Verrückungen ist jedoch, dass sie mit "der geometrischen Konfiguration des Systems verträglich" ist. Der Stab bleibt gerade - wir haben also nur eine unabhängige Koordinate im System. Wir können und müssen also entweder  
Allerdings haben wir zwei Koordinaten ''Δℓ'' und ''u<sub>1</sub>'' sowie deren Variationen. Die Forderung an die virtuellen Verrückungen ist jedoch, dass sie mit "der geometrischen Konfiguration des Systems verträglich" ist. Der Stab bleibt gerade - wir haben also nur eine unabhängige Koordinate im System. Wir können und müssen also entweder  


* u<sub>1</sub> durch ''Δℓ'' '' '' oder
* ''u<sub>1</sub>'' durch ''Δℓ'' oder
* ''Δℓ'' durch ''u<sub>1</sub>''
* ''Δℓ'' durch ''u<sub>1</sub>''


ausdrücken. Wir wählen ''u<sub>1</sub>'' als Minimal-Koordinate.<!-------------------------------------------------------------------------------->
ausdrücken. Wir wählen ''u<sub>1</sub>'' als Minimal-Koordinate.
 
{{MyCodeBlock|title=Gleichungen und Unbekannte
|text=Text
|code=
<syntaxhighlight lang="lisp" line start=1>
1+1
</syntaxhighlight>
}}
 


<!-------------------------------------------------------------------------------->
{{MyCodeBlock|title=Lösen
|text=
Einsetzten von ''Δℓ'' und seiner Variationen
Einsetzten von ''Δℓ'' und seiner Variationen


<math>\begin{array}{l}\mathit{\Delta \ell}=\sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}-{{\ell}_{0}}\\\mathit{\delta \ell}=\displaystyle\frac{{{u}_{1}}\cdot \mathit{\delta u}}{\sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}}\end{array}
::<math>\begin{array}{l}\mathit{\Delta \ell}=\sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}-{{\ell}_{0}}\\\mathit{\delta \ell}=\displaystyle\frac{{{u}_{1}}\cdot \mathit{\delta u}}{\sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}}\end{array}
</math>
</math>


liefert
liefert


<math>\mathit{\delta W}=-F\cdot \mathit{\delta u}-\displaystyle \frac{{{u}_{1}}\cdot \left( \sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}-\sqrt{{{u}_{0}^{2}}+{{h}_{0}^{2}}}\right) \cdot \mathit{EA}\cdot \mathit{\delta u}}{\sqrt{{{u}_{0}^{2}}+{{h}_{0}^{2}}}\cdot \sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}}
::<math>\mathit{\delta W}=-F\cdot \mathit{\delta u}-\displaystyle \frac{{{u}_{1}}\cdot \left( \sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}-\sqrt{{{u}_{0}^{2}}+{{h}_{0}^{2}}}\right) \cdot \mathit{EA}\cdot \mathit{\delta u}}{\sqrt{{{u}_{0}^{2}}+{{h}_{0}^{2}}}\cdot \sqrt{{{u}_{1}^{2}}+{{h}_{0}^{2}}}}
</math>
</math>


Zeile 117: Zeile 121:
Mit der Abkürzung <math>u_1 = \nu\cdot u_0</math> ist die Gleichgewichtsbeziehung:
Mit der Abkürzung <math>u_1 = \nu\cdot u_0</math> ist die Gleichgewichtsbeziehung:


<math>F=-\displaystyle \frac{\left( \nu\cdot \sqrt{{{\nu}^{2}}+4}-\sqrt{5}\cdot \nu\right) \cdot \mathit{EA}}{\sqrt{5}\cdot \sqrt{{{\nu}^{2}}+4}}</math>
::<math>F=-\displaystyle \frac{\left( \nu\cdot \sqrt{{{\nu}^{2}}+4}-\sqrt{5}\cdot \nu\right) \cdot \mathit{EA}}{\sqrt{5}\cdot \sqrt{{{\nu}^{2}}+4}}</math>
|code=
<syntaxhighlight lang="lisp" line start=1>
/* solve */
equ : subst(ref,subst(subst(disp,[PvV[2],PvV[3]]),PvV[1]));
equ : subst([u[1]= nu*u[0], u[0]=1],subst(params,equ));
equ: expand(subst(equ,δW))=0;
 
sol[1]: solve(equ,F)[1];
</syntaxhighlight>
}}


==tmp==
[[Datei:PvV2-21.png|mini|Stabkraft ''F'']]Beim Auftragen von ''F'' über ''u<sub>1</sub>'' sehen wir:


Um den Abstand zur Wand zu verringern (''u<sub>1</sub>'' kleiner zu machen) steigt die Kraft ''F'' zunächst, sinkt dann aber wieder auf Null. Das macht anschaulich Sinn - denn wenn der Stab im Extremfall senkrecht steht, brauchen wir (fast) keine Kraft aufzuwenden, um ihn weiter nach "links" zu verschieben. Im Gegenteil: bei einem Experiment würde der Stab durch seine Längskraft aus der vertikalen Lage herausgedrückt. <!-------------------------------------------------------------------------------->


<!-------------------------------------------------------------------------------->
{{MyCodeBlock|title=Ausdeuten der nichtlinearen Lösung
{{MyCodeBlock|title=Ausdeuten der nichtlinearen Lösung
|text=Text
|text=
[[Datei:PvV2-21.png|mini|Stabkraft ''F'']]Beim Auftragen von ''F'' über ''u<sub>1</sub>'' sehen wir:
 
Um den Abstand zur Wand zu verringern (''u<sub>1</sub>'' kleiner zu machen) steigt die Kraft ''F'' zunächst, sinkt dann aber wieder auf Null. Das macht anschaulich Sinn - denn wenn der Stab im Extremfall senkrecht steht, brauchen wir (fast) keine Kraft aufzuwenden, um ihn weiter nach "links" zu verschieben. Im Gegenteil: bei einem Experiment würde der Stab durch seine Längskraft aus der vertikalen Lage herausgedrückt.
|code=
|code=
<syntaxhighlight lang="lisp" line start=1>
<syntaxhighlight lang="lisp" line start=1>
1+1
/* postprocess */
plot2d(subst(sol[1],F/EA),[nu,0,1],
            [legend,false],
            [xlabel, "u1/u0 ->"], [ylabel, "F/EA->"]);
</syntaxhighlight>
</syntaxhighlight>
}}
}}


==tmp==
<!-------------------------------------------------------------------------------->
[[Datei:PvV2-22.png|mini|Verlgleich von linearer und nichtlinearer Lösung]]Ein wenig einfacher wird es, wenn wir kleine Auslenkungen ''u<sub>2</sub>'' um die entspannte Lage des Stabes herum betrachten also
{{MyCodeBlock|title=Linearisieren der Lösung
|text=
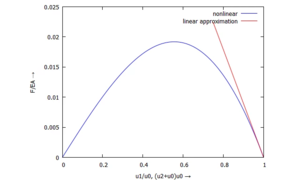
[[Datei:PvV2-22.png|mini|Vergleich von linearer und nichtlinearer Lösung]]Ein wenig einfacher wird es, wenn wir kleine Auslenkungen ''u<sub>2</sub>'' um die entspannte Lage des Stabes herum betrachten also<blockquote><blockquote><math>u_1 = u_0+u_2</math></blockquote></blockquote>Dann dürfen wir die kinematischen Beziehungen linearisieren, also


Dann dürfen wir die kinematischen Beziehungen linearisieren, also
::<math>\begin{array}{l}\mathit{\Delta \ell}=\displaystyle \frac{{{u}_{2}}}{\sqrt{5}},\\\mathit{\delta \ell}=\displaystyle \frac{\mathit{\delta u}}{\sqrt{5}}\end{array}</math>


und erhalten damit
und erhalten damit


Diesen Zusammenhang können wir als lineare Approximation in das Ergebnis oben eintragen:<!-------------------------------------------------------------------------------->
::<math>\displaystyle -F\cdot \mathit{\delta u}-\frac{{{u}_{2}}\cdot \mathit{EA}\cdot \mathit{\delta u}}{{{5}^{\frac{3}{2}}}\cdot {{u}_{0}}}=0</math>


{{MyCodeBlock|title=Linearisieren der Lösung
Diesen Zusammenhang können wir als lineare Approximation in das Ergebnis oben eintragen:
|text=Text
|code=
|code=
<syntaxhighlight lang="lisp" line start=1>
<syntaxhighlight lang="lisp" line start=1>
1+1
/* postprocess: linearize solution */
lindisp: subst([u[1]=u[0]+u[2]],subst(ref,disp[1]));
lindisp: subst([u[2]=0],lindisp)+subst([u[2]=0],diff(lindisp,u[2]))*u[2];
lindisp: subst(params,lindisp);
lindisp: [lindisp, subst([Δl=δl, u[2]=δu],lindisp)];
equ : subst(params,subst(ref,subst(subst(lindisp,[PvV[2],PvV[3]]),PvV[1])));
equ: expand(subst(equ,δW))=0;
sol[2]: solve(equ,F)[1];
 
plot2d([[parametric, t, subst([nu=t],subst(sol[1],F/EA)),[t,0,1]],
        [parametric, 1+t, subst([u[2]=t*u[0]],subst(sol[2],F/EA)),[t,-1/4,0]]],
            [legend,"nonlinear", "linear approximation"],
            [xlabel, "u1/u0, (u2+u0)u0 →"], [ylabel, "F/EA →"]);
</syntaxhighlight>
</syntaxhighlight>
}}
}}
<table class="wikitable" style="background-color:white; float: left; margin-right:14px;
">
<tr><th></th><th></th></tr>
<tr><td></td><td></td></tr>
</table>


<hr/>
<hr/>

Aktuelle Version vom 2. April 2021, 13:37 Uhr


Aufgabenstellung

Hier setzen wir unsere Untersuchung aus PvV1 fort: nun bauen wir eine elastische "Leiter" ein, die durch die Kraft F gestaucht wird. Die Problemstellung lautet:

Ein elastischer Stab (Dehnsteifigkeit EA, Länge ℓ0) ist bei A eingekeilt und steht bei B auf einer reibungsfreien Rolle.

Lageplan

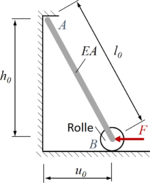
Gesucht ist die Kraft F auf das Stabende als Funktion der horizontalen Verschiebung von Punkt B mit dem Prinzip der virtuellen Verrückungen.

In der gezeichneten Ausgangslage ist der Stab spannungsfrei.

Lösung mit Maxima

Lageplan

Koordinaten

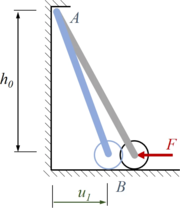
Hier ist die Leiter mit der Koordinate u1 von Punkt B gezeichnet. Bei der Variation um δu wandert der Angriffspunktspunkt B der Kraft F also in horizontaler Richtung. 


/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 15.08.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2017-10-08                            */
/* ref: TM-C, PvV mit elastischen Körpern              */
/* description: finds the displacement u employing PvV */
/*******************************************************/
 
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δΠ", alphabetic);
declare("Δl", alphabetic);
declare("δl", alphabetic);
declare("δu", alphabetic);
declare("δη", alphabetic);

assume(EA > 0, l[0]>0, h[0]>0, u[0]>0);
/* parameter */
params: [h[0]=2*u[0]];




Kinematik

Über den Satz des Pythagoras bekommen wir einen Zusammenhang zwischen der Verschiebung u1 und der Stablängung Δℓ:

Für die Variation δℓ von Δℓ führen wir die Hilfsgröße ε als Koeffizient von δu ein. Da die virtuelle Verrückung "differentiell klein" sein darf, nehmen wir nur das lineare Glied bzgl. δu und bekommen mit

den Ausdruck

.

Der Zusammenhang ist nichtlinear! Das ist anschaulich klar - liefert hier jedoch komplizierte Formeln .... 


/* Kinematik: */
kinematics: (l[0]+Δl)^2 = h[0]^2+u[1]^2;
ref: solve(l[0]^2 = h[0]^2+u[0]^2,l[0])[2];
/* displacemant and variation */
disp: solve(kinematics,Δl)[2];
disp: [disp, δl=subst(0,epsilon,
        diff(subst([u[1] = u[1]+epsilon*δu],subst(disp,Δl)),
                                                    epsilon))];




Gleichgewicht

In das Gleichgewicht gehen alle Arbeiten am System ein.

Im Unterschied zu einem Kräftegleichgewicht fallen hier alle Lager-Reaktionskräfte herus: in A und B verschwindet nämlich das Skalarprodukt des virtuellen Verschiebungsvektors mit den Normalkräften auf die Wände - sie stehen senkrecht aufeinander. Im Vergleich zu PvV1 müssen wir allerdings die virtuelle Formänderungsenergie δΠ berücksichtigen: 


/* equilibrium condition */
PvV: [δW=δW^a-δΠ,
      δW^a = -F*δu,
      δΠ = EA/l[0]*Δl*δl];




Gleichungen und Unbekannte

Mit der Gleichung oben haben wir genau eine Gleichung für F - das passt!.

Allerdings haben wir zwei Koordinaten Δℓ und u1 sowie deren Variationen. Die Forderung an die virtuellen Verrückungen ist jedoch, dass sie mit "der geometrischen Konfiguration des Systems verträglich" ist. Der Stab bleibt gerade - wir haben also nur eine unabhängige Koordinate im System. Wir können und müssen also entweder

  • u1 durch Δℓ oder
  • Δℓ durch u1

ausdrücken. Wir wählen u1 als Minimal-Koordinate.

Lösen

Einsetzten von Δℓ und seiner Variationen

liefert

Charakteristisch ist dabei, dass sich die Variation - hier der Stab-Längung Δℓ - herauskürzt: sie dient nur zur Identifikation einer Gleichgewichtsbeziehung. Das wird wichtig, wenn wir mehrere Unbekannten und Koordinaten haben - dann ist der Koeffizient vor jeder Variation einer Koordinate eine Gleichgewichtsbeziehung. Jetzt macht die Aussage Sinn, dass sie "gedachte, voneinander unabhängige Verschiebungen" sind!

Mit der Abkürzung  ist die Gleichgewichtsbeziehung: 


/* solve */
equ : subst(ref,subst(subst(disp,[PvV[2],PvV[3]]),PvV[1]));
equ : subst([u[1]= nu*u[0], u[0]=1],subst(params,equ));
equ: expand(subst(equ,δW))=0;

sol[1]: solve(equ,F)[1];





Ausdeuten der nichtlinearen Lösung

Stabkraft F

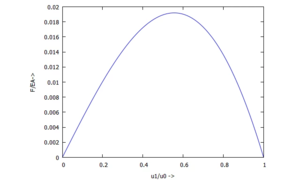
Beim Auftragen von F über u1 sehen wir:

Um den Abstand zur Wand zu verringern (u1 kleiner zu machen) steigt die Kraft F zunächst, sinkt dann aber wieder auf Null. Das macht anschaulich Sinn - denn wenn der Stab im Extremfall senkrecht steht, brauchen wir (fast) keine Kraft aufzuwenden, um ihn weiter nach "links" zu verschieben. Im Gegenteil: bei einem Experiment würde der Stab durch seine Längskraft aus der vertikalen Lage herausgedrückt. 


/* postprocess */
plot2d(subst(sol[1],F/EA),[nu,0,1],
             [legend,false],
             [xlabel, "u1/u0 ->"], [ylabel, "F/EA->"]);




Linearisieren der Lösung

Vergleich von linearer und nichtlinearer Lösung

Ein wenig einfacher wird es, wenn wir kleine Auslenkungen u2 um die entspannte Lage des Stabes herum betrachten also

Dann dürfen wir die kinematischen Beziehungen linearisieren, also

und erhalten damit

Diesen Zusammenhang können wir als lineare Approximation in das Ergebnis oben eintragen: 


/* postprocess: linearize solution */
lindisp: subst([u[1]=u[0]+u[2]],subst(ref,disp[1]));
lindisp: subst([u[2]=0],lindisp)+subst([u[2]=0],diff(lindisp,u[2]))*u[2];
lindisp: subst(params,lindisp);
lindisp: [lindisp, subst([Δl=δl, u[2]=δu],lindisp)];
equ : subst(params,subst(ref,subst(subst(lindisp,[PvV[2],PvV[3]]),PvV[1])));
equ: expand(subst(equ,δW))=0;
sol[2]: solve(equ,F)[1];

plot2d([[parametric, t, subst([nu=t],subst(sol[1],F/EA)),[t,0,1]],
        [parametric, 1+t, subst([u[2]=t*u[0]],subst(sol[2],F/EA)),[t,-1/4,0]]],
             [legend,"nonlinear", "linear approximation"],
             [xlabel, "u1/u0, (u2+u0)u0 →"], [ylabel, "F/EA →"]);




Links

  • ...

Literature

  • ...
Abgerufen von „https://numpedia.rzbt.haw-hamburg.de/index.php?title=Gelöste_Aufgaben/PvV2&oldid=3063“