Gelöste Aufgaben/Kw99: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „k“ |
Keine Bearbeitungszusammenfassung |
||
| (11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
k | [[Category:Gelöste Aufgaben]] | ||
[[Category:Dimensionslose Schreibweise]] | |||
[[Category:Analytische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Biege-Belastung]] | |||
[[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Maxima]] | |||
==Aufgabenstellung== | |||
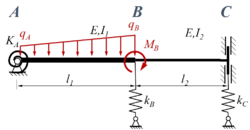
Ein Stab ''ABC'' ist durch eine lineare veränderliche Streckenlast ''q'' mit den Eckwerten ''q<sub>A</sub>'' in ''A'' und ''q<sub>B</sub>'' in ''B'' sowie dem Moment ''M<sub>B</sub>'' in ''B'' belastet. Der Stab (E-Modul: ''E'') besteht aus zwei Sektionen mit den Längen ''l<sub>1</sub>'' bzw. ''l<sub>2</sub>'' sowie den Flächenmomenten ''I<sub>1</sub>'' bzw. ''I<sub>2</sub>''. Der Stab ist in ''A'' durch ein gelenkiges Festlager, in ''C'' durch eine Schiebehülse gelagert, in ''B'' sind die beiden Sektionen fest miteinander verbunden. Die Feder in ''A'' ist eine Drehfester mit Steifigkeit ''K<sub>A</sub>'', die Federn in ''B'' und ''C'' sind Translationsfedern mit den Steifigkeiten ''k<sub>B</sub>, k<sub>C</sub>''. | |||
<onlyinclude> | |||
[[Datei:Kw98-01.png|alternativtext=|links|mini|250x250px|Lageplan]] | |||
Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken. Im Vergleich zu [[Gelöste Aufgaben/Kw98|Kw98]] wird hier eine Lösung mit normierten Koordinaten verfolgt. | |||
</onlyinclude> | |||
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter: | |||
::<math>\begin{array}{ll}\displaystyle {{\mathit{EI}}_{2}}&=\frac{{{\mathit{EI}}_{1}}}{2},\\ {{K}_{A}}&=\displaystyle \frac{{{\mathit{EI}}_{1}}}{{{\ell}_{1}}},\\ {{k}_{B}}&=0,\\ {{k}_{C}}&=\displaystyle \frac{{{\mathit{EI}}_{1}}}{{{\ell}_{1}^{3}}},\\ {{q}_{B}}&=4\cdot {{q}_{A}},\\ {{\ell}_{2}}&=\displaystyle \frac{{{\ell}_{1}}}{2},\\ {{M}_{B}}&=5\cdot {{\ell}_{1}^{2}}\cdot {{q}_{A}}\end{array}</math>. | |||
== Lösung mit Maxima == | |||
Die Aufgabe ist ein klassisches Randwertproblem: | |||
# zwei Gebiete, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast ''q'' belastet ist (in Bereich II ist die Streckenlast allerdings Null) und somit durch die Differentialbeziehung<blockquote><math>E\; I_i w_i^{IV}(x_i) = q(x_i) ,\;\; i=\{1,2\}</math></blockquote>berschrieben wird. | |||
# Rand- und Übergangsbedingungen in den Punkten A, B, C | |||
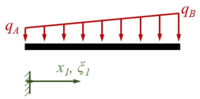
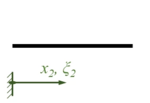
Wir verwenden ''x<sub>i</sub>'' und ''ξ<sub>i</sub>'' als Koordinaten je Bereich, in der Übersicht sieht das Randwertproblem so aus:<table class="wikitable" style="background-color:white;"> | |||
<tr><th>Rand<br />A</th><th>Bereich I</th><th>Übergang<br />B</th><th>Bereich II</th><th>Rand<br />C</th></tr> | |||
<tr><td></td><td>[[Datei:Kw98-11AB.png|rahmenlos|alternativtext=|200x200px]]</td><td></td><td>[[Datei:Kw98-11BC.png|rahmenlos|alternativtext=|150x150px]]</td><td></td></tr> | |||
<tr><td>[[Datei:Kw98-11A.png|116x116px|rahmenlos|alternativtext=]]</td><td></td><td>[[Datei:Kw98-11B.png|rahmenlos|alternativtext=|128x128px]]</td><td></td><td>[[Datei:Kw98-11C.png|rahmenlos|alternativtext=|140x140px]] | |||
</td></tr> | |||
</table> | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text= | |||
Diese Aufgabe wird mit der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten Elemente]] in [[Gelöste Aufgaben/Kw96|KW96]] gelöst. Und im Vergleich zu [[Gelöste Aufgaben/Kw98|KW98]] wird hier die analytische Lösung mit dimensionslosen Koordinaten angeschreiben. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2017-09-06 */ | |||
/* ref: TM-C, Labor 1 - dimensionslos */ | |||
/* description: die Auslenkung w und die unabhängige */ | |||
/* Ortskoordinate werden dim'los gemacht */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
Wir definieren die Formfunktionen für die Streckenlast | |||
::<math>\begin{array}{l}{{\phi}_{0}}\left( \xi\right) :=1-\xi\\{{\phi}_{1}}\left( \xi\right) :=\xi\end{array} \text{ mit } \xi = \displaystyle\frac{x_1}{\ell_1}</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* system parameter */ | |||
params: [EI[2]=EI[1]/2, | |||
K[A]=EI[1]/l[1], | |||
k[B]=0, | |||
k[C] = EI[1]/l[1]^3, | |||
q[B]=4*q[A], | |||
l[2]=l[1]/2, | |||
M[B] = 5*q[A]*l[1]^2]; | |||
/* form - functions */ | |||
phi[0](xi) := 1 - xi; | |||
phi[1](xi) := xi; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Integration of Differential Equation to Formfunction | |||
|text= | |||
In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung | |||
::<math>E\; I_i w_i^{IV}(x_i) = q(x_i) ,\;\; i=\{1,2\} \text{ mit } q(x_i) = q_0\cdot\phi_0(\xi) + q_1\cdot\phi_1(\xi)</math>, | |||
die wir durch Integration lösen und dann bereichsweise an Rand- und Übergangsbedingungen anpassen. Diese Aufgabe wird etwas übersichtlicher, wenn wir die Auslenkung ''w'' und die Ortskoordinate ''x'' dimensionslos machen. So wählen wir: | |||
::<math>w = \ell_{Bez}\cdot \tilde{w}</math> | |||
und setzten für die Bezugslänge die Auslenkung eines Kragbalkens unter konstanter Streckenlast (hier ''q<sub>A</sub>'') an. Diese Auslenkung findet man in [[Sources/Lexikon/Standard-Lösungen|Standard-Lösungen]] unter "Kragbalken mit Streckenlast" zu: | |||
::<math>{{\ell}_{\mathit{Bez}}}=\displaystyle \frac{{{q}_{A}} \cdot {{\ell}_{1}^{4}}}{8\cdot {{\mathit{EI}}_{1}}}</math> | |||
Zusätzlich wählen wir zwei unabhängige, dimensionslose Ortskoordinaten für die Bereich I und II, die ihren Ursprung jeweils in den Punkten A und B haben. | |||
::<math>\xi_i = \displaystyle \frac{x_i}{\ell_i}</math> | |||
Mit | |||
::<math>\begin{array}{lll}q_0=q_A, &q_1=q_B &\text{ für Bereich I und}\\q_0=0, &q_1=0 &\text{ für Bereich II}\end{array}</math> | |||
ist die allgemeine Lösung für | |||
::<math>\begin{array}{ll} \ldots\text{ die Verdrehung: }&\displaystyle \phi_i(x) = \frac{d\,w_i(x)}{d\,x_i}\\ \ldots\text{ das Biege-Moment: }&\displaystyle M_i(x) = - EI_i \frac{d^2\,w_i(x)}{d\,x_i^2}\\ \ldots\text{ die Querkraft: }&\displaystyle Q_i(x) = - EI_i \frac{d^3\,w_i(x)}{d\,x_i^3} \end{array}</math> | |||
... für Bereich I: | |||
::<math>\begin{array}{ll} {{w}_{1}}\left( \xi\right) :=&\frac{120\cdot {{C}_{1,0}}\cdot {{\ell}_{\mathit{Bez}}}+120\cdot {{C}_{1,1}}\cdot {{\ell}_{\mathit{Bez}}}\cdot \xi+60\cdot {{C}_{1,2}}\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{2}}+20\cdot {{C}_{1,3}}\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{3}}+\left( 5\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{4}}-{{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{5}}\right) \cdot {{q}_{A}}+{{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{5}}\cdot {{q}_{B}}}{15\cdot {{q}_{A}}}\\ {{\phi}_{1}}\left( \xi\right) :=&\frac{120\cdot {{C}_{1,1}}\cdot {{\ell}_{\mathit{Bez}}}+120\cdot {{C}_{1,2}}\cdot {{\ell}_{\mathit{Bez}}}\cdot \xi+60\cdot {{C}_{1,3}}\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{2}}+\left( 20\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{3}}-5\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{4}}\right) \cdot {{q}_{A}}+5\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{4}}\cdot {{q}_{B}}}{15\cdot {{\ell}_{1}}\cdot {{q}_{A}}}\\ {{M}_{1}}\left( \xi\right) :=&-\frac{{{\mathit{EI}}_{1}}\cdot \left( 120\cdot {{C}_{1,2}}\cdot {{\ell}_{\mathit{Bez}}}+120\cdot {{C}_{1,3}}\cdot {{\ell}_{\mathit{Bez}}}\cdot \xi+\left( 60\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{2}}-20\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{3}}\right) \cdot {{q}_{A}}+20\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{3}}\cdot {{q}_{B}}\right) }{15\cdot {{\ell}_{1}^{2}}\cdot {{q}_{A}}}\\ {{Q}_{1}}\left( \xi\right) :=&-\frac{{{\mathit{EI}}_{1}}\cdot \left( 120\cdot {{C}_{1,3}}\cdot {{\ell}_{\mathit{Bez}}}+\left( 120\cdot {{\ell}_{\mathit{Bez}}}\cdot \xi-60\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{2}}\right) \cdot {{q}_{A}}+60\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{2}}\cdot {{q}_{B}}\right) }{15\cdot {{\ell}_{1}^{3}}\cdot {{q}_{A}}} \end{array}</math> | |||
... für Bereich II: | |||
::<math>\begin{array}{ll} {{w}_{2}}\left( \xi\right) :=&\frac{24\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,0}}\cdot {{\ell}_{\mathit{Bez}}}+24\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,1}}\cdot {{\ell}_{\mathit{Bez}}}\cdot \xi+12\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,2}}\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{2}}+4\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,3}}\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{3}}}{3\cdot {{\ell}_{1}^{4}}\cdot {{\mathit{EI}}_{2}}\cdot {{q}_{A}}}\\ {{\phi}_{2}}\left( \xi\right) :=&\frac{24\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,1}}\cdot {{\ell}_{\mathit{Bez}}}+24\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,2}}\cdot {{\ell}_{\mathit{Bez}}}\cdot \xi+12\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,3}}\cdot {{\ell}_{\mathit{Bez}}}\cdot {{\xi}^{2}}}{3\cdot {{\ell}_{1}^{4}}\cdot {{\ell}_{2}}\cdot {{\mathit{EI}}_{2}}\cdot {{q}_{A}}}\\ {{M}_{2}}\left( \xi\right) :=&-\frac{24\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,2}}\cdot {{\ell}_{\mathit{Bez}}}+24\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,3}}\cdot {{\ell}_{\mathit{Bez}}}\cdot \xi}{3\cdot {{\ell}_{1}^{4}}\cdot {{\ell}_{2}^{2}}\cdot {{q}_{A}}}\\ {{Q}_{2}}\left( \xi\right) :=&-\frac{8\cdot {{\mathit{EI}}_{1}}\cdot {{\ell}_{2}}\cdot {{C}_{2,3}}\cdot {{\ell}_{\mathit{Bez}}}}{{{\ell}_{1}^{4}}\cdot {{q}_{A}}} \end{array}</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* solve ....*/ | |||
dimless : l[Bez] = q[A]*l[1]^4/(8*EI[1]); | |||
dgl : EI[i]*l[Bez]*diff(w(xi),xi,4)/l[i]^4 = q[0]*phi[0](xi) + q[1]*phi[1](xi); | |||
dgl: subst(dimless,dgl); | |||
/* generic solution */ | |||
displ : solve(integrate(integrate(integrate(integrate(dgl,xi),xi),xi),xi),w(xi)); | |||
sections: [[i=1, %c4=C[1,0], %c3=C[1,1], %c2=C[1,2], %c1=C[1,3], q[0]=q[A], q[1]=q[B]], | |||
[i=2, %c4=C[2,0], %c3=C[2,1], %c2=C[2,2], %c1=C[2,3], q[0]= 0 , q[1]= 0 ]]; | |||
/* section I */ | |||
define( w[1](xi), ratsimp(subst(sections[1],subst(displ,l[Bez]*w(xi))))); | |||
define(Phi[1](xi), diff(w[1](xi),xi )/l[1]^1); | |||
define( M[1](xi), -EI[1]*diff(w[1](xi),xi,2)/l[1]^2); | |||
define( Q[1](xi), -EI[1]*diff(w[1](xi),xi,3)/l[1]^3); | |||
/* section II */ | |||
define( w[2](xi), ratsimp(subst(sections[2],subst(displ,l[Bez]*w(xi))))); | |||
define(Phi[2](xi), diff(w[2](xi),xi )/l[2]^1); | |||
define( M[2](xi), -EI[2]*diff(w[2](xi),xi,2)/l[2]^2); | |||
define( Q[2](xi), -EI[2]*diff(w[2](xi),xi,3)/l[2]^3); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Boundary Conditions | |||
|text= | |||
Für die 2*4 = 8 Integrationskonstanten | |||
::<math>\left[ C_{1,0},C_{1,1},C_{1,2},C_{1,3},C_{2,0},C_{2,1},C_{2,2},C_{2,3}\right]</math> | |||
suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen. | |||
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten A, B, C und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen. | |||
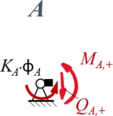
====Aus Rand "A"==== | |||
<table class="wikitable" style="background-color:white;"> | |||
<tr><td>[[Datei:Kw98-11A.png|rahmenlos|alternativtext=|134x134px]] | |||
</td><td>''Geometrische Randbedingungen'' | |||
# <math>w_1(0)=0</math> | |||
''Kraft- und Momenten-Randbedingungen'' | |||
#<math>K_A\cdot \phi_A + M_{A,+} = 0 \text{ mit } M_{A,+} = - EI_1\cdot w''(x)|_{x=0}</math> | |||
</td></tr> | |||
</table> | |||
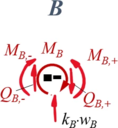
====Aus Übergang "B"==== | |||
<table class="wikitable" style="background-color:white;"> | |||
<tr><td>[[Datei:Kw98-11B.png|rahmenlos|alternativtext=|162x162px]] | |||
</td><td>''Geometrische Randbedingungen'' | |||
#<math>w_1(\ell_1)=w_2(\ell_1)</math> | |||
#<math>\phi_1(\ell_1) = \phi_2(\ell_1)</math> | |||
''Kraft- und Momenten-Randbedingungen'' | |||
#<math>-M_{B,-} - M_{B} + M_{B,+} = 0</math> | |||
#<math>-Q_{B,-}-k_B\cdot w_B + -Q_{B,+} = 0</math> | |||
</td></tr> | |||
</table> | |||
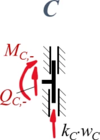
====Aus Rand "C"==== | |||
<table class="wikitable" style="background-color:white;"> | |||
<tr><td>[[Datei:Kw98-11C.png|rahmenlos|alternativtext=|154x154px]] | |||
</td><td>''Geometrische Randbedingungen'' | |||
#<math>\phi_2(\ell_2)=0</math> | |||
''Kraft- und Momenten-Randbedingungen'' | |||
#<math>-Q_{C,-} -k_C\cdot w_C = 0</math> | |||
</td></tr> | |||
</table> | |||
Und das liefert das Gleichungssystem aus 8 Gleichungen | |||
::<math>\begin{array}{ccc}{{C}_{1,0}}&=&0\\ \frac{{{\ell}_{1}}\cdot {{C}_{1,1}}\cdot {{K}_{A}}}{{{\mathit{EI}}_{1}}}-{{C}_{1,2}}&=&0\\ \frac{{{q}_{B}}}{120}+\frac{{{q}_{A}}}{30}+\frac{{{C}_{1,3}}}{6}+\frac{{{C}_{1,2}}}{2}+{{C}_{1,1}}+{{C}_{1,0}}&=&\frac{{{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{4}}\cdot {{C}_{2,0}}}{{{\ell}_{1}^{4}}\cdot {{\mathit{EI}}_{2}}}\\ \frac{{{q}_{B}}}{24}+\frac{{{q}_{A}}}{8}+\frac{{{C}_{1,3}}}{2}+{{C}_{1,2}}+{{C}_{1,1}}&=&\frac{{{\mathit{EI}}_{1}}\cdot {{\ell}_{2}^{3}}\cdot {{C}_{2,1}}}{{{\ell}_{1}^{3}}\cdot {{\mathit{EI}}_{2}}}\\ \frac{{{q}_{B}}}{2}-\frac{{{\ell}_{2}^{4}}\cdot {{C}_{2,0}}\cdot {{k}_{B}}}{{{\ell}_{1}}\cdot {{\mathit{EI}}_{2}}}+\frac{{{q}_{A}}}{2}-\frac{{{\ell}_{2}}\cdot {{C}_{2,3}}}{{{\ell}_{1}}}+{{C}_{1,3}}&=&0\\ -\frac{{{M}_{B}}}{{{\ell}_{1}^{2}}}+\frac{{{q}_{B}}}{6}+\frac{{{q}_{A}}}{3}-\frac{{{\ell}_{2}^{2}}\cdot {{C}_{2,2}}}{{{\ell}_{1}^{2}}}+{{C}_{1,3}}+{{C}_{1,2}}&=&0\\ \frac{{{\ell}_{2}^{3}}\cdot {{C}_{2,3}}}{2\cdot {{\ell}_{1}^{3}}}+\frac{{{\ell}_{2}^{3}}\cdot {{C}_{2,2}}}{{{\ell}_{1}^{3}}}+\frac{{{\ell}_{2}^{3}}\cdot {{C}_{2,1}}}{{{\ell}_{1}^{3}}}&=&0\\ -\frac{{{\ell}_{2}^{4}}\cdot {{C}_{2,3}}\cdot {{k}_{C}}}{6\cdot {{\ell}_{1}}\cdot {{\mathit{EI}}_{2}}}-\frac{{{\ell}_{2}^{4}}\cdot {{C}_{2,2}}\cdot {{k}_{C}}}{2\cdot {{\ell}_{1}}\cdot {{\mathit{EI}}_{2}}}-\frac{{{\ell}_{2}^{4}}\cdot {{C}_{2,1}}\cdot {{k}_{C}}}{{{\ell}_{1}}\cdot {{\mathit{EI}}_{2}}}-\frac{{{\ell}_{2}^{4}}\cdot {{C}_{2,0}}\cdot {{k}_{C}}}{{{\ell}_{1}}\cdot {{\mathit{EI}}_{2}}}+\frac{{{\ell}_{2}}\cdot {{C}_{2,3}}}{{{\ell}_{1}}}&=&0\end{array} | |||
</math> | |||
für die Integrationskonstanten. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* boundary conditions */ | |||
node[A]: [ w[1](0) = 0, | |||
K[A]*Phi[1](0)+M[1](0) = 0]; | |||
node[B]: [ w[1](1) = w[2](0), | |||
Phi[1](1) = Phi[2](0), | |||
-Q[1](1) -k[B]*w[2](0) +Q[2](0) = 0, | |||
-M[1](1) -M[B]+M[2](0) = 0]; | |||
node[C]: [ Phi[2](1) = 0, | |||
-Q[2](1) - k[C]*w[2](1) = 0]; | |||
BCs : expand(subst(dimless,append(node[A],node[B],node[C]))); | |||
scale: [EI[1]/l[1]^4, 1/l[1]^2, EI[1]/l[1]^4, EI[1]/l[1]^3,1/l[1], 1/l[1]^2, EI[2]/l[1]^3, 1/l[1]]; | |||
BCs : expand(scale*BCs); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Prepare for Solver | |||
|text= | |||
Das Gleichungssystem wollen wir als | |||
::<math>\underline{\underline{A}}\cdot\underline{x}= \underline{b} | |||
</math> | |||
schreiben, also - hier nach Einsetzen der System-Parameter | |||
::<math>\begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & -1 & 0 & 0 & 0 & 0 & 0\\ 1 & 1 & \frac{1}{2} & \frac{1}{6} & -\frac{1}{8} & 0 & 0 & 0\\ 0 & 1 & 1 & \frac{1}{2} & 0 & -\frac{1}{4} & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & -\frac{1}{2}\\ 0 & 0 & 1 & 1 & 0 & 0 & -\frac{1}{4} & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{1}{8} & \frac{1}{8} & \frac{1}{16}\\ 0 & 0 & 0 & 0 & -\frac{1}{8} & -\frac{1}{8} & -\frac{1}{16} & \frac{23}{48}\end{pmatrix}\cdot \underline{x}=\begin{pmatrix}0\\ 0\\ -\frac{{{q}_{A}}}{15}\\ -\frac{7\cdot {{q}_{A}}}{24}\\ -\frac{5\cdot {{q}_{A}}}{2}\\ 4\cdot {{q}_{A}}\\ 0\\ 0\end{pmatrix} | |||
</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* integration constants = unknowns */ | |||
ICs : [C[1,0],C[1,1],C[1,2],C[1,3],C[2,0],C[2,1],C[2,2],C[2,3]]; | |||
ACM: augcoefmatrix(BCs,ICs); | |||
/* system matrix and rhs */ | |||
AA : submatrix(ACM,9); | |||
bb : - col(ACM,9); | |||
/* print OLE */ | |||
print(subst(params,AA),"*",x,"=",subst(params,bb)); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text= | |||
Das Lösen des Gleichungssystems liefert | |||
::<math>\begin{array}{l} {{C}_{1,0}}=0,\\{{C}_{1,1}}=\frac{1331\cdot {{q}_{A}}}{1170},\\{{C}_{1,2}}=\frac{1331\cdot {{q}_{A}}}{1170},\\{{C}_{1,3}}=-\frac{257\cdot {{q}_{A}}}{1365},\\{{C}_{2,0}}=\frac{57058\cdot {{q}_{A}}}{4095},\\{{C}_{2,1}}=\frac{81007\cdot {{q}_{A}}}{8190},\\{{C}_{2,2}}=-\frac{9994\cdot {{q}_{A}}}{819},\\{{C}_{2,3}}=\frac{6311\cdot {{q}_{A}}}{1365} \end{array} | |||
</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* solving */ | |||
D : ratsimp(determinant(AA))$ | |||
[ P, L, U] : ratsimp(get_lu_factors(lu_factor(AA)))$ | |||
cc : ratsimp(linsolve_by_lu(AA,bb)[1])$ | |||
sol : makelist(ICs[i] = cc[i][1],i,1,8)$ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
Und die Ergebnisse können wir uns anschauen ... | |||
==== ... für w(x): ==== | |||
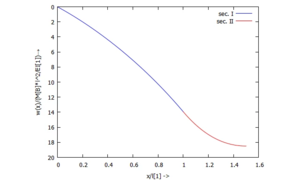
[[Datei:Kw99-21.png|mini|Biegelinie ''w(x)''|alternativtext=|ohne]] | |||
==== ... für ''Φ(x)'': ==== | |||
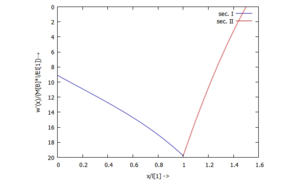
[[Datei:Kw99-22.png|mini|Kippung ''w'(x)''|alternativtext=|ohne]] | |||
==== ... für M(x): ==== | |||
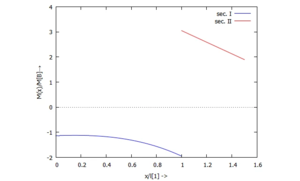
[[Datei:Kw99-23.png|mini|Biegemoment M(x)|alternativtext=|ohne]] | |||
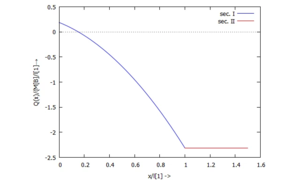
==== ... für Q(x): ==== | |||
[[Datei:Kw99-24.png|mini|Querkraft ''Q(x)''|alternativtext=|ohne]] | |||
====... für die Lager-Reaktionskräfte:==== | |||
::<math>\begin{array}{ll} {{A}_{z}}&=\frac{257\cdot {{\ell}_{1}}\cdot {{q}_{A}}}{1365},\\{{M}_{A}}&=\frac{1331\cdot {{\ell}_{1}^{2}}\cdot {{q}_{A}}}{1170},\\{{B}_{z}}&=0,\\{{C}_{z}}&=\frac{6311\cdot {{\ell}_{1}}\cdot {{q}_{A}}}{2730},\\{{M}_{C}}&=\frac{31037\cdot {{\ell}_{1}^{2}}\cdot {{q}_{A}}}{16380} \end{array}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/* bearing forces and moments */ | |||
reactForces: [A[z] = Q[1](0), | |||
M[A] = K[A]*Phi[1](0), | |||
B[z] = k[B]*w[2](0), | |||
C[z] = k[C]*w[2](1), | |||
M[C] = M[2](1)]; | |||
expand(subst(dimless,subst(params,subst(sol, reactForces)))); | |||
/* plot displacements */ | |||
fcts: [[ w [1](xi), w [2](xi)], | |||
[Phi[1](xi),Phi[2](xi)], | |||
[ M [1](xi), M [2](xi)], | |||
[ Q [1](xi), Q [2](xi)]]; | |||
facts: [1/l[Bez], l[1]/l[Bez], 1/(q[A]*l[1]^2), 1/(q[A]*l[1])]; | |||
textlabels : ["w(x)/(M[B]*l^2/EI[1])→", "w'(x)/(M[B]*l/EI[1])→", "M(x)/M[B]→", "Q(x)/(M[B]/l[1]→"]; | |||
for i: 1 thru 4 do( | |||
f : expand(subst(dimless,subst(params,facts[i]*[subst(sol, fcts[i][1]), | |||
subst(sol, fcts[i][2])]))), | |||
r : subst(params,l[2]/l[1]), | |||
preamble: if i<=2 then "set yrange [] reverse" else "set yrange []", | |||
plot2d([[parametric, t, subst(t,xi,f[1]), [t,0,1]], | |||
[parametric, 1+r*t, subst(t,xi,f[2]), [t,0,1]]], | |||
[legend, "sec. I", "sec. II"], | |||
[gnuplot_preamble, preamble], | |||
[xlabel, "x/l[1] ->"], | |||
[ylabel, textlabels[i]]))$ | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 31. März 2021, 13:47 Uhr
Aufgabenstellung
Ein Stab ABC ist durch eine lineare veränderliche Streckenlast q mit den Eckwerten qA in A und qB in B sowie dem Moment MB in B belastet. Der Stab (E-Modul: E) besteht aus zwei Sektionen mit den Längen l1 bzw. l2 sowie den Flächenmomenten I1 bzw. I2. Der Stab ist in A durch ein gelenkiges Festlager, in C durch eine Schiebehülse gelagert, in B sind die beiden Sektionen fest miteinander verbunden. Die Feder in A ist eine Drehfester mit Steifigkeit KA, die Federn in B und C sind Translationsfedern mit den Steifigkeiten kB, kC.
Gesucht ist die analytische Lösung für den Euler-Bernoulli-Balken. Im Vergleich zu Kw98 wird hier eine Lösung mit normierten Koordinaten verfolgt.
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:
- .
Lösung mit Maxima
Die Aufgabe ist ein klassisches Randwertproblem:
- zwei Gebiete, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast q belastet ist (in Bereich II ist die Streckenlast allerdings Null) und somit durch die Differentialbeziehungberschrieben wird.
- Rand- und Übergangsbedingungen in den Punkten A, B, C
Wir verwenden xi und ξi als Koordinaten je Bereich, in der Übersicht sieht das Randwertproblem so aus:
| Rand A | Bereich I | Übergang B | Bereich II | Rand C |
|---|---|---|---|---|
 |  | |||
 |  | 
|
Header
Diese Aufgabe wird mit der Methode der Finiten Elemente in KW96 gelöst. Und im Vergleich zu KW98 wird hier die analytische Lösung mit dimensionslosen Koordinaten angeschreiben.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-09-06 */
/* ref: TM-C, Labor 1 - dimensionslos */
/* description: die Auslenkung w und die unabhängige */
/* Ortskoordinate werden dim'los gemacht */
/*******************************************************/
Declarations
Wir definieren die Formfunktionen für die Streckenlast
- .
/* system parameter */
params: [EI[2]=EI[1]/2,
K[A]=EI[1]/l[1],
k[B]=0,
k[C] = EI[1]/l[1]^3,
q[B]=4*q[A],
l[2]=l[1]/2,
M[B] = 5*q[A]*l[1]^2];
/* form - functions */
phi[0](xi) := 1 - xi;
phi[1](xi) := xi;
Integration of Differential Equation to Formfunction
In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung
- ,
die wir durch Integration lösen und dann bereichsweise an Rand- und Übergangsbedingungen anpassen. Diese Aufgabe wird etwas übersichtlicher, wenn wir die Auslenkung w und die Ortskoordinate x dimensionslos machen. So wählen wir:
und setzten für die Bezugslänge die Auslenkung eines Kragbalkens unter konstanter Streckenlast (hier qA) an. Diese Auslenkung findet man in Standard-Lösungen unter "Kragbalken mit Streckenlast" zu:
Zusätzlich wählen wir zwei unabhängige, dimensionslose Ortskoordinaten für die Bereich I und II, die ihren Ursprung jeweils in den Punkten A und B haben.
Mit
ist die allgemeine Lösung für
... für Bereich I:
... für Bereich II:
- .
/* solve ....*/
dimless : l[Bez] = q[A]*l[1]^4/(8*EI[1]);
dgl : EI[i]*l[Bez]*diff(w(xi),xi,4)/l[i]^4 = q[0]*phi[0](xi) + q[1]*phi[1](xi);
dgl: subst(dimless,dgl);
/* generic solution */
displ : solve(integrate(integrate(integrate(integrate(dgl,xi),xi),xi),xi),w(xi));
sections: [[i=1, %c4=C[1,0], %c3=C[1,1], %c2=C[1,2], %c1=C[1,3], q[0]=q[A], q[1]=q[B]],
[i=2, %c4=C[2,0], %c3=C[2,1], %c2=C[2,2], %c1=C[2,3], q[0]= 0 , q[1]= 0 ]];
/* section I */
define( w[1](xi), ratsimp(subst(sections[1],subst(displ,l[Bez]*w(xi)))));
define(Phi[1](xi), diff(w[1](xi),xi )/l[1]^1);
define( M[1](xi), -EI[1]*diff(w[1](xi),xi,2)/l[1]^2);
define( Q[1](xi), -EI[1]*diff(w[1](xi),xi,3)/l[1]^3);
/* section II */
define( w[2](xi), ratsimp(subst(sections[2],subst(displ,l[Bez]*w(xi)))));
define(Phi[2](xi), diff(w[2](xi),xi )/l[2]^1);
define( M[2](xi), -EI[2]*diff(w[2](xi),xi,2)/l[2]^2);
define( Q[2](xi), -EI[2]*diff(w[2](xi),xi,3)/l[2]^3);
Boundary Conditions
Für die 2*4 = 8 Integrationskonstanten
suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen.
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten A, B, C und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen.
Aus Rand "A"
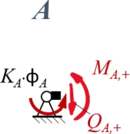
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen |
Aus Übergang "B"
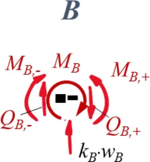
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen |
Aus Rand "C"
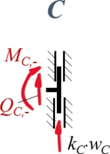
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen |
Und das liefert das Gleichungssystem aus 8 Gleichungen
für die Integrationskonstanten.
/* boundary conditions */
node[A]: [ w[1](0) = 0,
K[A]*Phi[1](0)+M[1](0) = 0];
node[B]: [ w[1](1) = w[2](0),
Phi[1](1) = Phi[2](0),
-Q[1](1) -k[B]*w[2](0) +Q[2](0) = 0,
-M[1](1) -M[B]+M[2](0) = 0];
node[C]: [ Phi[2](1) = 0,
-Q[2](1) - k[C]*w[2](1) = 0];
BCs : expand(subst(dimless,append(node[A],node[B],node[C])));
scale: [EI[1]/l[1]^4, 1/l[1]^2, EI[1]/l[1]^4, EI[1]/l[1]^3,1/l[1], 1/l[1]^2, EI[2]/l[1]^3, 1/l[1]];
BCs : expand(scale*BCs);
Prepare for Solver
Das Gleichungssystem wollen wir als
schreiben, also - hier nach Einsetzen der System-Parameter
/* integration constants = unknowns */
ICs : [C[1,0],C[1,1],C[1,2],C[1,3],C[2,0],C[2,1],C[2,2],C[2,3]];
ACM: augcoefmatrix(BCs,ICs);
/* system matrix and rhs */
AA : submatrix(ACM,9);
bb : - col(ACM,9);
/* print OLE */
print(subst(params,AA),"*",x,"=",subst(params,bb));
Solving
Das Lösen des Gleichungssystems liefert
/* solving */
D : ratsimp(determinant(AA))$
[ P, L, U] : ratsimp(get_lu_factors(lu_factor(AA)))$
cc : ratsimp(linsolve_by_lu(AA,bb)[1])$
sol : makelist(ICs[i] = cc[i][1],i,1,8)$
Post-Processing
Und die Ergebnisse können wir uns anschauen ...
... für w(x):
... für Φ(x):
... für M(x):
... für Q(x):
... für die Lager-Reaktionskräfte:
/* bearing forces and moments */
reactForces: [A[z] = Q[1](0),
M[A] = K[A]*Phi[1](0),
B[z] = k[B]*w[2](0),
C[z] = k[C]*w[2](1),
M[C] = M[2](1)];
expand(subst(dimless,subst(params,subst(sol, reactForces))));
/* plot displacements */
fcts: [[ w [1](xi), w [2](xi)],
[Phi[1](xi),Phi[2](xi)],
[ M [1](xi), M [2](xi)],
[ Q [1](xi), Q [2](xi)]];
facts: [1/l[Bez], l[1]/l[Bez], 1/(q[A]*l[1]^2), 1/(q[A]*l[1])];
textlabels : ["w(x)/(M[B]*l^2/EI[1])→", "w'(x)/(M[B]*l/EI[1])→", "M(x)/M[B]→", "Q(x)/(M[B]/l[1]→"];
for i: 1 thru 4 do(
f : expand(subst(dimless,subst(params,facts[i]*[subst(sol, fcts[i][1]),
subst(sol, fcts[i][2])]))),
r : subst(params,l[2]/l[1]),
preamble: if i<=2 then "set yrange [] reverse" else "set yrange []",
plot2d([[parametric, t, subst(t,xi,f[1]), [t,0,1]],
[parametric, 1+r*t, subst(t,xi,f[2]), [t,0,1]]],
[legend, "sec. I", "sec. II"],
[gnuplot_preamble, preamble],
[xlabel, "x/l[1] ->"],
[ylabel, textlabels[i]]))$
Links
- ...
Literature
- ...