Gelöste Aufgaben/Kerb: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (32 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:Anfangswertproblem]] | |||
[[Category:Ansys]][[Category:Shell-Element]] | |||
[[Category:Prinzip der virtuellen Verrückungen]] | |||
[[Category:Dynamik]][[Category:D’Alembertsches Prinzip]] | |||
[[Category:Maxima]] | |||
[[Category:Nichtlineare Schwingungen]] | |||
[[Category:Starrer Körper]] | |||
==Aufgabenstellung== | |||
<onlyinclude> | |||
[[Datei:Kerb-01.png|150px|left]] | |||
Ein Satellit soll eine stabile Umlaufbahn um die Erde beschreiben. | |||
Gesucht sind mögliche Lösungen. | |||
</onlyinclude> | |||
[[ | == Lösung mit Maxima == | ||
Bei unserer Suche geht es um kartesische- und polare-Koordinatensysteme, Gleichgewichtsbedingungen formuliert mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] und er Stabilität von Lösungen. | |||
[[ | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | ||
|text=Ein Satellit im Orbit ist einer Erdbeschleunigung g ausgesetzt, die nichtlinear von seinem Abstand zum Erdmittelpunkt abhängt. Dieses nichtlineare Anfangswertproblem lösen wir hier als [[Anfangswertprobleme|Anfangswertproblem]] numerisch. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*********************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2018-03-21 */ | |||
/* ref: Kerb (TM-C, Labor 6) */ | |||
/* description: finds persiod solution for */ | |||
/* the tracectory of a satellite */ | |||
/*********************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | |||
|text= | |||
Wir brauchen die Systemparameter | |||
[[Datei:Kerb-16.png|mini|Weg-Zeit-Diagramm]] | <table class="wikitable"> | ||
<tr><th>Symbol</th><th>Bedeutung</th></tr> | |||
<tr><td>R = 6378,137 km</td><td>Erdradius am Äquator</td></tr> | |||
<tr><td>g<sub>0</sub> = 9.81 m/s2</td><td>Erdbeschleunigung an der Erdoberfläche</td></tr> | |||
<tr><td>T = 1 d</td><td>Periodendauer einer Erdumdrehung (d .. day)</td></tr> | |||
<tr><td>O<sub>r</sub> = 35786 km</td><td>Höhe eines Satelliten über der Erdoberfläche in einem geostationären Orbit.</td></tr> | |||
</table> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*********************************************************/ | |||
/* declarations */ | |||
/* declare variational variables - see 6.3 Identifiers */ | |||
declare("δW", alphabetic); | |||
declare("δr", alphabetic); | |||
declare("δu", alphabetic); | |||
declare("δφ", alphabetic); | |||
assume(R>0, g>0, rho>0, mu>0, T>0); | |||
/* parameter */ | |||
params: [R = 6378137*m, /* earth radius at equator */ | |||
g = 9.81*m/s^2, /* gravitational constant */ | |||
T = 24*60*60*s]; /* 24 hours */ | |||
verify: [O=R+35786000*m]; /* geostat. orbit */ | |||
dimles: [g=mu*R/T^2]; /* dimensionless parameter */ | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Kinematics | |||
|text=Wir führen ein kartesisches ''x, y, z'' - Koordinaten-System im Erdmittelpunkt ([[wikipedia:Earth-centered_inertial|earth-centered inertial]]) ein, das nicht mit der Erde mitrotiert - wir setzen dieses als Intertialsystem an (obwohl wir wissen, dass die Erde um die Sonne rotiert und die Sonne selbst auch kein Intertialsystem in unserem Sinne ist). [[Datei:Kerb-01.png|mini|Satellite in Orbit|alternativtext=|links]]Wir brauchen die Einheitsvektoren | |||
::<math>\vec{e}_x, \vec{e}_y</math> | |||
entlang der x,y-Achsen, um den Ortsvektor zum Satelliten | |||
::<math>\vec{r} = r(t) \cdot \vec{e}_r(t)</math> | |||
zu erfassen. | |||
Dafür verwenden wir | |||
::<math>\vec{e}_r(t) = \cos(\varphi(t))\cdot\vec{e}_x + \sin(\varphi(t))\cdot\vec{e}_y</math>. | |||
Die Bewegung des Satelliten können wir also auch in kartesischen Koordinarten | |||
::<math>\begin{array}{l}u_x(t) = r(t) \cdot \cos(\varphi(t))\\u_y(t) = r(t) \cdot \sin(\varphi(t))\end{array}</math>, | |||
anschreiben, was hier allerdings wenig anschaulich ist! Für die Variation von ''u<sub>x</sub>, u<sub>y</sub>'' erhalten wir | |||
::<math>\begin{array}{l} \delta u_x = \cos(\varphi(t))\cdot\delta r - r(t)\cdot \sin(\varphi(t))\cdot\delta \varphi\\ \delta u_y = \sin(\varphi(t))\cdot\delta r + r(t)\cdot\cos(\varphi(t))\cdot \delta \varphi \end{array}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/******************************************/ | |||
/* kinematics */ | |||
/******************************************/ | |||
kinem : [u[x] = r(t) * cos(phi(t)), u[y] = r(t) * sin(phi(t))]; | |||
varia : [r(t) = r(t) + epsilon*δr, phi(t) = phi(t) + epsilon*δφ]; | |||
varia : [δu[x],δu[y]] = subst([epsilon=0],diff(subst(varia,subst(kinem,[u[x],u[y]])),epsilon)); | |||
kinem : append(makelist(lhs(varia)[i] = rhs(varia)[i],i,1,2), kinem); | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Die Bewegungsgleichungen schreiben wir mit dem Prinzip der virtuellen Verrückungen an, hier mit den Anteilen der D'Alembert'sche Trägheitskräfte und der Gewichtskraft | |||
::<math>\delta W = \underbrace{- m \cdot \ddot{u}_x(t)\cdot \delta u_x - m \cdot \ddot{u}_y(t)\cdot \delta u_y}_{\text{d'Alembert'sche Trägheitskräfte}} \;\;\; \underbrace{- m \, g(r)\cdot \delta r}_{\text{Gewichtskraft}}</math>, | |||
dabei ist ''m'' die Masse des Satelliten - die sich aber sofort herauskürzt. | |||
In die Gleichgewichtsbedingung | |||
::<math>\delta W \stackrel{!}{=}0</math> | |||
setzen wir alle Größen ein und finden | |||
::<math>\delta W= \displaystyle -\frac{\left( g_0\, m\, {{R}^{2}}+m\cdot {r^{2}}\, \ddot{r}(t) -m\cdot {r^{3}}\, \dot{\varphi}^{2}\right) \, \delta r +\left( 2\, m\cdot {r^{3}}\, \dot{\varphi} \, \dot{r} + m\cdot r^{4} \, \ddot{\varphi} \right) \, \delta \varphi}{{r^{2}}}</math>. | |||
Das Trennen nach den virtuellen Verrückungen liefert dann die beiden Bewegungsgleichungen | |||
::<math>\begin{array}{cl} \displaystyle -r \cdot \dot{\varphi}^2 + \ddot{r} + g_0 \cdot \left(\frac{R}{r}\right)^2& = 0,\\ -2\, r \cdot \dot{\varphi} \cdot \dot{r} - r^2 \cdot \ddot{\varphi} &= 0 \end{array}</math>. | |||
Für die dimensionslose Schreibweise setzen wir | |||
::<math>\begin{array}{ll} t & = \tau \cdot T\\ r(t) & = \rho(t) \cdot R\\ \end{array}</math> | |||
an und verwenden die Abkürzungen | |||
::<math>\begin{array}{ll} \displaystyle \frac{d}{d\tau}\varphi & = \Phi \\ \displaystyle \frac{d}{d\rho}\varphi & = P \end{array}</math>, | |||
wobei das P für das große griechische ρ steht. Damit - und mit dem dimensionslosen Parameter ''μ'' statt | |||
::<math>\displaystyle g = \frac{\mu\,R}{T^2}</math> | |||
lesen sich die beiden Bewegungsgleichungen so: | |||
::<math>\begin{array}{ll} \displaystyle \frac{d}{d\tau} P &\displaystyle = \frac{\Phi^2 \, \rho^3-\mu}{\rho^2} \\ \displaystyle \frac{d}{d\rho} \Phi & = \displaystyle - 2 \frac{\Phi \, P}{\rho} \end{array}</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/******************************************/ | |||
/* define ODE in dim'less coordinates */ | |||
/******************************************/ | |||
/* principle of virtual work */ | |||
PvV: δW = - m*'diff(u[x],t,2)*δu[x] - m*'diff(u[y],t,2)*δu[y] - m*g*(R/r(t))^2*δr; | |||
PvV: subst(kinem, PvV); | |||
PvV: trigsimp(expand(ev(PvV,nouns))); | |||
/* equations of motion */ | |||
eom: makelist(ev(coeff(expand(subst(PvV,δW)), [δr, δφ][i]),nouns),i,1,2); | |||
/* transformation to dimensionless coordinates */ | |||
trafo: [diff( r(t),t,2) = R*'diff(Rho,tau)/T^2, diff( r(t),t) = R*Rho/T, | |||
diff(phi(t),t,2) = 'diff(Phi,tau)/T^2, diff(phi(t),t) = Phi/T, | |||
r(t) = rho*R, phi(t) = phi ]; | |||
eom : ratsimp(solve(subst(trafo,eom), ['diff(Rho,tau),'diff(Phi,tau)]))[1]; | |||
eom : ratsimp(subst(dimles,eom)); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Stationary Solution | |||
|text=Für den stationären Orbit ist | |||
::<math>\displaystyle \frac{d}{d\tau} P^* = 0 \text{ und } P^* = 0 | |||
</math>, | |||
also | |||
::<math>\displaystyle \Phi^* = \sqrt{\frac{\mu}{\rho^3}}</math>. | |||
Hier wählen wir als stationäre Lösung den [[wikipedia:Geostationary_orbit|geostationären Orbit]] - der Satellit dreht sich dann in ''T'' = einem Tag einmal um den Erdmittelpunkt und erscheint so von einem Betrachter auf der Erde als "fest"-stehend. Die dazugehörige Drehgeschwindigkeit in dimensionsloser Koordinate ist | |||
::<math>\displaystyle \Phi^* \stackrel{!}{=} \frac{2\pi}{1}</math> | |||
und damit | |||
::<math>\displaystyle \rho^* = \sqrt[3]{\frac{\mu}{4\pi^2}}</math> | |||
Dieser Wert stimmt gut mit bekannten Werten für die Höhe des [[wikipedia:Geostationary_orbit|geostationären Orbits]] (''O'' = 35.786 km s.o.) überein. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/******************************************/ | |||
/* stationary solution (dphi/dt = 2*%pi/T)*/ | |||
/* (geostationary orbit) for .... */ | |||
/******************************************/ | |||
geostat : solve(rhs(eom[1])=0,Phi)[2]; | |||
geostat : [geostat,solve(subst(geostat, Phi = 2*%pi),rho)[3]]; | |||
geostat : append(geostat, subst(params,solve(dimles,mu))); | |||
test: float(subst(params,subst(geostat,rho)=subst(verify,O)/R)); | |||
eom : append(['diff(rho,tau)=Rho,'diff(phi,tau)=Phi],eom); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text= | |||
Die dimensionslosen Zustandsgrößen des Satelliten sind | |||
::<math>\underline{q} = \left(\begin{array}{c}\rho\\\varphi\\P\\\Phi\end{array}\right)</math>. | |||
Die Bewegungsgleichungen können wir nun als Anfangswertproblem numerisch lösen. Wir wählen zwei Tage als Integrationsdauer, als Löser ein Runge-Kutta-Verfahren sowie drei verschiedene Anfangsbedingungen. Davon ist die erste (blau) die geostationäre Lösung. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/******************************************/ | |||
/* numerical solution of IVP */ | |||
/******************************************/ | |||
/* state variables */ | |||
Q : [rho,phi,Rho,Phi]; | |||
states: [r,p,v,o]; | |||
/* smapling characteristics */ | |||
times : subst([t0 = 0, tmax = 2, dt = 0.001], | |||
[t, t0, tmax, dt]); | |||
/* initial values */ | |||
init : [[subst(geostat,rho),0,0,2.0*%pi], | |||
[6,0,0,2.0*%pi], | |||
[7,0,0,2.0*%pi]]; | |||
/* transformation to nomenclature with is "digestible" for maxima */ | |||
newnom: makelist(Q[j]=states[j],j,1,4); | |||
/* right-hand-side for the integration routine */ | |||
dydt : subst(newnom,subst(params,makelist(rhs(subst(solve(dimles,mu),eom[i])),i,1,4))); | |||
/* test: does that work? */ | |||
test: subst(makelist(states[j]=init[1][j],j,1,4),dydt); | |||
/* integrate for all sets of initial values */ | |||
for i: 1 thru length(init) do | |||
num[i] : rk(dydt,states,init[i],times)$ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
Wir sehen, dass der Satellit bei der blauen - geostationären - Lösung in der Tat eine Kreisbahn um den Erdmittelpunkt beschriebt. Werden Anfangsbedingungen näher am Erdmittelpunkt (rot) oder weiter entfernt davon (grün) gewählt, so ergeben sich weiterhin periodische Lösungen, allerdings keine kreisförmigen Lösungen mehr um den Erdmittelpunkt. | |||
<table class="wikitable"> | |||
<tr><th>Orbit</th><th>Animation</th></tr> | |||
<tr><td>[[Datei:Kerb-11.png|250px|mini|Orbits (nicht maßstäblich).]]</td><td>[[Datei:Kerb-12 video 1280.mp4|mini|Trajectory animation]]</td></tr> | |||
</table> | |||
In den Phasen-Diagrammen für die Lösungen kann man gut erkennen, wie sich dabei die Geschwindigkeiten über euinen Umlauf ändern. | |||
[[Datei:Kerb-Phase-Diagrams.png|ohne|mini|Phasen-Diagramme]] | |||
Analog können wir die Winkelgeschwindigkeit Φ über der Radialgeschwindigkeit P auftragen: | |||
[[Datei:Kerb-15.png|ohne|mini|Phasengeschwindigkeit]] | |||
Und wir können uns sowohl die Koordinate ρ also auch die Winkelgeschwindigkeit Φ im Zeitbereich ansehen: | |||
[[Datei:Kerb-16.png|ohne|left|mini|Weg-Zeit-Diagramm]] | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/******************************************/ | |||
/* post-processing */ | |||
/******************************************/ | |||
for i: 1 thru length(init) do | |||
(T[i] : makelist(num[i][j][1],j,1,length(num[i])), | |||
r[i] : makelist(num[i][j][2],j,1,length(num[i])), | |||
p[i] : makelist(num[i][j][3],j,1,length(num[i])), | |||
v[i] : makelist(num[i][j][4],j,1,length(num[i])), | |||
o[i] : makelist(num[i][j][5],j,1,length(num[i])))$ | |||
/* set print-precision */ | |||
fpprintprec: 4$ | |||
/* plot results */ | |||
/* - orbits */ | |||
orbits: makelist([discrete, r[i]*cos(p[i]), r[i]*sin(p[i])],i,1,length(init))$ | |||
legends: append([legend], makelist(sconcat("start @: ",string(float(init[i]))),i,1,length(init)))$ | |||
plot2d(orbits, | |||
[xlabel,"u/R →"], [ylabel,"v/R →"], [legend, "geostat.", "var. 1", "var 2"], [title, "Orbits"], same_xy)$ | |||
/* - phase diagrams */ | |||
phases : makelist([discrete, r[i], v[i]],i,1,length(init))$ | |||
plot2d(phases, | |||
[xlabel,"r/1 →"], [ylabel,"P/1 →"], legends, | |||
[title, "Phase Digram for radial coord."])$ | |||
/* - speed diagrams */ | |||
v_o : makelist([discrete, v[i], o[i]],i,1,length(init))$ | |||
plot2d(v_o, [xlabel,"v/1 →"], [ylabel,"o/1 →"], legends)$ | |||
/* - time - radius / angular speed */ | |||
ro_t : append(makelist([discrete, T[i], r[i]],i,1,length(init)), | |||
makelist([discrete, T[i], o[i]],i,1,length(init)))$ | |||
plot2d(ro_t, [style, [lines,1,1], [lines,1,2], [lines,1,3], [lines,2,1], [lines,2,2], [lines,2,3]], | |||
[xlabel,"tau/1 →"], [ylabel,"r/1 →"], [legend, "r geostat.", "r var. 1", "r var 2","o","o","o"])$ | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
'''Links''' | |||
* [https://www.kerbalspaceprogram.com/ Kerbala Space Program] | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 27. März 2021, 07:52 Uhr
Aufgabenstellung
Ein Satellit soll eine stabile Umlaufbahn um die Erde beschreiben.
Gesucht sind mögliche Lösungen.
Lösung mit Maxima
Bei unserer Suche geht es um kartesische- und polare-Koordinatensysteme, Gleichgewichtsbedingungen formuliert mit dem Prinzip der virtuellen Verrückungen und er Stabilität von Lösungen.
Header
Ein Satellit im Orbit ist einer Erdbeschleunigung g ausgesetzt, die nichtlinear von seinem Abstand zum Erdmittelpunkt abhängt. Dieses nichtlineare Anfangswertproblem lösen wir hier als Anfangswertproblem numerisch.
/*********************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-03-21 */
/* ref: Kerb (TM-C, Labor 6) */
/* description: finds persiod solution for */
/* the tracectory of a satellite */
/*********************************************************/
Declarations
Wir brauchen die Systemparameter
| Symbol | Bedeutung |
|---|---|
| R = 6378,137 km | Erdradius am Äquator |
| g0 = 9.81 m/s2 | Erdbeschleunigung an der Erdoberfläche |
| T = 1 d | Periodendauer einer Erdumdrehung (d .. day) |
| Or = 35786 km | Höhe eines Satelliten über der Erdoberfläche in einem geostationären Orbit. |
/*********************************************************/
/* declarations */
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δr", alphabetic);
declare("δu", alphabetic);
declare("δφ", alphabetic);
assume(R>0, g>0, rho>0, mu>0, T>0);
/* parameter */
params: [R = 6378137*m, /* earth radius at equator */
g = 9.81*m/s^2, /* gravitational constant */
T = 24*60*60*s]; /* 24 hours */
verify: [O=R+35786000*m]; /* geostat. orbit */
dimles: [g=mu*R/T^2]; /* dimensionless parameter */
Kinematics
Wir führen ein kartesisches x, y, z - Koordinaten-System im Erdmittelpunkt (earth-centered inertial) ein, das nicht mit der Erde mitrotiert - wir setzen dieses als Intertialsystem an (obwohl wir wissen, dass die Erde um die Sonne rotiert und die Sonne selbst auch kein Intertialsystem in unserem Sinne ist).
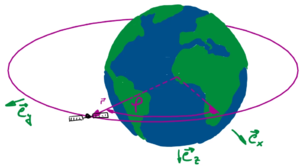
Wir brauchen die Einheitsvektoren
entlang der x,y-Achsen, um den Ortsvektor zum Satelliten
zu erfassen.
Dafür verwenden wir
- .
Die Bewegung des Satelliten können wir also auch in kartesischen Koordinarten
- ,
anschreiben, was hier allerdings wenig anschaulich ist! Für die Variation von ux, uy erhalten wir
/******************************************/
/* kinematics */
/******************************************/
kinem : [u[x] = r(t) * cos(phi(t)), u[y] = r(t) * sin(phi(t))];
varia : [r(t) = r(t) + epsilon*δr, phi(t) = phi(t) + epsilon*δφ];
varia : [δu[x],δu[y]] = subst([epsilon=0],diff(subst(varia,subst(kinem,[u[x],u[y]])),epsilon));
kinem : append(makelist(lhs(varia)[i] = rhs(varia)[i],i,1,2), kinem);
Equilibrium Conditions
Die Bewegungsgleichungen schreiben wir mit dem Prinzip der virtuellen Verrückungen an, hier mit den Anteilen der D'Alembert'sche Trägheitskräfte und der Gewichtskraft
- ,
dabei ist m die Masse des Satelliten - die sich aber sofort herauskürzt.
In die Gleichgewichtsbedingung
setzen wir alle Größen ein und finden
- .
Das Trennen nach den virtuellen Verrückungen liefert dann die beiden Bewegungsgleichungen
- .
Für die dimensionslose Schreibweise setzen wir
an und verwenden die Abkürzungen
- ,
wobei das P für das große griechische ρ steht. Damit - und mit dem dimensionslosen Parameter μ statt
lesen sich die beiden Bewegungsgleichungen so:
- .
/******************************************/
/* define ODE in dim'less coordinates */
/******************************************/
/* principle of virtual work */
PvV: δW = - m*'diff(u[x],t,2)*δu[x] - m*'diff(u[y],t,2)*δu[y] - m*g*(R/r(t))^2*δr;
PvV: subst(kinem, PvV);
PvV: trigsimp(expand(ev(PvV,nouns)));
/* equations of motion */
eom: makelist(ev(coeff(expand(subst(PvV,δW)), [δr, δφ][i]),nouns),i,1,2);
/* transformation to dimensionless coordinates */
trafo: [diff( r(t),t,2) = R*'diff(Rho,tau)/T^2, diff( r(t),t) = R*Rho/T,
diff(phi(t),t,2) = 'diff(Phi,tau)/T^2, diff(phi(t),t) = Phi/T,
r(t) = rho*R, phi(t) = phi ];
eom : ratsimp(solve(subst(trafo,eom), ['diff(Rho,tau),'diff(Phi,tau)]))[1];
eom : ratsimp(subst(dimles,eom));
Stationary Solution
Für den stationären Orbit ist
- ,
also
- .
Hier wählen wir als stationäre Lösung den geostationären Orbit - der Satellit dreht sich dann in T = einem Tag einmal um den Erdmittelpunkt und erscheint so von einem Betrachter auf der Erde als "fest"-stehend. Die dazugehörige Drehgeschwindigkeit in dimensionsloser Koordinate ist
und damit
Dieser Wert stimmt gut mit bekannten Werten für die Höhe des geostationären Orbits (O = 35.786 km s.o.) überein.
/******************************************/
/* stationary solution (dphi/dt = 2*%pi/T)*/
/* (geostationary orbit) for .... */
/******************************************/
geostat : solve(rhs(eom[1])=0,Phi)[2];
geostat : [geostat,solve(subst(geostat, Phi = 2*%pi),rho)[3]];
geostat : append(geostat, subst(params,solve(dimles,mu)));
test: float(subst(params,subst(geostat,rho)=subst(verify,O)/R));
eom : append(['diff(rho,tau)=Rho,'diff(phi,tau)=Phi],eom);
Solving
Die dimensionslosen Zustandsgrößen des Satelliten sind
- .
Die Bewegungsgleichungen können wir nun als Anfangswertproblem numerisch lösen. Wir wählen zwei Tage als Integrationsdauer, als Löser ein Runge-Kutta-Verfahren sowie drei verschiedene Anfangsbedingungen. Davon ist die erste (blau) die geostationäre Lösung.
/******************************************/
/* numerical solution of IVP */
/******************************************/
/* state variables */
Q : [rho,phi,Rho,Phi];
states: [r,p,v,o];
/* smapling characteristics */
times : subst([t0 = 0, tmax = 2, dt = 0.001],
[t, t0, tmax, dt]);
/* initial values */
init : [[subst(geostat,rho),0,0,2.0*%pi],
[6,0,0,2.0*%pi],
[7,0,0,2.0*%pi]];
/* transformation to nomenclature with is "digestible" for maxima */
newnom: makelist(Q[j]=states[j],j,1,4);
/* right-hand-side for the integration routine */
dydt : subst(newnom,subst(params,makelist(rhs(subst(solve(dimles,mu),eom[i])),i,1,4)));
/* test: does that work? */
test: subst(makelist(states[j]=init[1][j],j,1,4),dydt);
/* integrate for all sets of initial values */
for i: 1 thru length(init) do
num[i] : rk(dydt,states,init[i],times)$
Post-Processing
Wir sehen, dass der Satellit bei der blauen - geostationären - Lösung in der Tat eine Kreisbahn um den Erdmittelpunkt beschriebt. Werden Anfangsbedingungen näher am Erdmittelpunkt (rot) oder weiter entfernt davon (grün) gewählt, so ergeben sich weiterhin periodische Lösungen, allerdings keine kreisförmigen Lösungen mehr um den Erdmittelpunkt.
| Orbit | Animation |
|---|---|
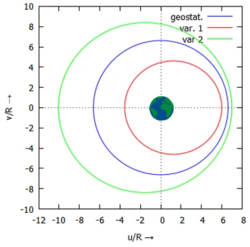 |
In den Phasen-Diagrammen für die Lösungen kann man gut erkennen, wie sich dabei die Geschwindigkeiten über euinen Umlauf ändern.
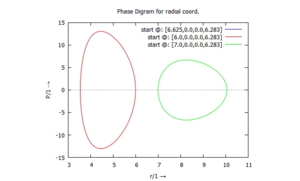
Analog können wir die Winkelgeschwindigkeit Φ über der Radialgeschwindigkeit P auftragen:
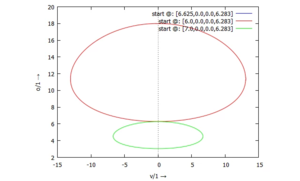
Und wir können uns sowohl die Koordinate ρ also auch die Winkelgeschwindigkeit Φ im Zeitbereich ansehen:
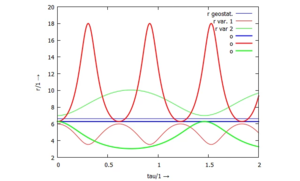
/******************************************/
/* post-processing */
/******************************************/
for i: 1 thru length(init) do
(T[i] : makelist(num[i][j][1],j,1,length(num[i])),
r[i] : makelist(num[i][j][2],j,1,length(num[i])),
p[i] : makelist(num[i][j][3],j,1,length(num[i])),
v[i] : makelist(num[i][j][4],j,1,length(num[i])),
o[i] : makelist(num[i][j][5],j,1,length(num[i])))$
/* set print-precision */
fpprintprec: 4$
/* plot results */
/* - orbits */
orbits: makelist([discrete, r[i]*cos(p[i]), r[i]*sin(p[i])],i,1,length(init))$
legends: append([legend], makelist(sconcat("start @: ",string(float(init[i]))),i,1,length(init)))$
plot2d(orbits,
[xlabel,"u/R →"], [ylabel,"v/R →"], [legend, "geostat.", "var. 1", "var 2"], [title, "Orbits"], same_xy)$
/* - phase diagrams */
phases : makelist([discrete, r[i], v[i]],i,1,length(init))$
plot2d(phases,
[xlabel,"r/1 →"], [ylabel,"P/1 →"], legends,
[title, "Phase Digram for radial coord."])$
/* - speed diagrams */
v_o : makelist([discrete, v[i], o[i]],i,1,length(init))$
plot2d(v_o, [xlabel,"v/1 →"], [ylabel,"o/1 →"], legends)$
/* - time - radius / angular speed */
ro_t : append(makelist([discrete, T[i], r[i]],i,1,length(init)),
makelist([discrete, T[i], o[i]],i,1,length(init)))$
plot2d(ro_t, [style, [lines,1,1], [lines,1,2], [lines,1,3], [lines,2,1], [lines,2,2], [lines,2,3]],
[xlabel,"tau/1 →"], [ylabel,"r/1 →"], [legend, "r geostat.", "r var. 1", "r var 2","o","o","o"])$
Links
Literature
- ...