Gelöste Aufgaben/Kw23: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „j“ |
Keine Bearbeitungszusammenfassung |
||
| (13 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
j | [[Category:Gelöste Aufgaben]] | ||
[[Category:Dimensionslose Schreibweise]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Anfangswertproblem]] | |||
[[Category:Feder-Masse-System]] | |||
[[Category:Dynamik]][[Category:D’Alembertsches Prinzip]] | |||
[[Category:Kennlinie]] | |||
[[Category:Maxima]] | |||
[[Category:Runge-Kutta-Verfahren]] | |||
[[Category:Nichtlineare Schwingungen]] | |||
==Aufgabenstellung== | |||
Eine Kugel (Masse m, Radius r) wird aus der Höhe H im Erdschwerefeld losgelassen, kommt auf den Boden auf und „springt“ dann wie ein Flummi auf und ab. Der Stoß zwischen Kugel und Oberfläche sei ideal-elastisch. Gefragt ist eine numerische Lösung des Problems als Anfangswertproblem. | |||
Dabei modellieren Sie die Kugel als elastisch, die Unterlage als starr. Die Kugel können Sie sich so wie unten skizziert im unteren Teil durch eine Feder ersetzt denken.<onlyinclude> | |||
[[Datei:Kw23-01.png|alternativtext=|links|mini|119x119px|Lageplan]] | |||
Eine elastische Kugel wird im Erdschwerefeld losgelassen und „springt“ wie ein Flummi auf und ab. Gesucht ist die numerische Lösung als Anfangswertproblem. | |||
</onlyinclude> | |||
== Lösung mit Maxima == | |||
Die Schwierigkeit kommt aus der Modellierung der Kontaktkraft zwischen Boden und Kugel. Oft reicht es, ein [https://de.wikipedia.org/wiki/Ph%C3%A4nomenologie phänomenologisches Modell] zu implementieren - also die Kontaktkraft als reine "Federkraft" zu interpretieren. | |||
<table class="wikitable" style="background-color:white; float: right;"> | |||
<tr><th colspan="2">Kugel-Modell: elastischer Kontakt<br/> mit Einfederung ''w''. | |||
</th></tr> | |||
<tr><td style="text-align:center">[[Datei:KW23-02.png|rahmenlos]]<br/><br/><br/></td> | |||
<td style="text-align:center">[[Datei:Kw23-03.png|rahmenlos]]</td></tr> | |||
</table> | |||
Die Federkraft K ist also Null, solange die Kugel die Oberfläche nicht berührt und sie sei hier - eine weitere drastische Vereinfachung - proportional zur Federkompression ''w'', wenn sich Kugel und Oberfläche berühren: | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Wir lösen das Anfangswertproblem zu einer nichtlinearen Bewegungsgleichung. Die Nichtlinearität kommt aus der Kontaktbedingung der Kugel mit der Oberfläche. | |||
Die Bewegungsgleichung ist stückweise linear, hier erfassen wir sie durch eine Kennlinie, die wir zwischen den linearen Bereich ausrunden. Das Ausrunden macht die numerische Integration schneller. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*********************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2017-09-24 */ | |||
/* ref: Kw23 (TM-C, Labor 5) */ | |||
/* description: finds the solution for */ | |||
/* the nonlinear IVP */ | |||
/*********************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
Wir verwenden die Parameter | |||
::<math>\begin{array}{ll}k &= \displaystyle \kappa \frac{m\;g}{r}\\t_{B} &=\sqrt{\displaystyle\frac{r}{g}}\\\kappa&=100\end{array}</math> | |||
[[Datei:Kw23-11.png|mini|Kontakt-Kennlinie]]Die [[Sources/Lexikon/Kontaktkennlinie|Kennlinie für den Kontakt]] definieren wir stückweise zu | |||
::<math>K(w,\epsilon) = \left\{ \begin{array}{ccl} 0 &\text{für}& w < -\epsilon\\ \displaystyle k\cdot\frac{\epsilon}{4} \left( 1+ \frac{w}{\epsilon} \right)^2 &\text{für}& -\epsilon < w<+\epsilon\\ k\cdot w &\text{für}& \epsilon < w\\ \end{array} \right.</math> | |||
Und so sieht sie dann aus: | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*********************************************************/ | |||
/* declarations */ | |||
assume(g>0, r>0); | |||
/* parameter */ | |||
params: [k = kappa*m*g/r, /*spring stiffness*/ | |||
t[B] = sqrt(2*r/g), /*reference time*/ | |||
kappa = 100]; /*dim'less spring stiffness*/ | |||
/**** define nonlinear spring characteristic ***/ | |||
K(w,epsilon) := if w <- epsilon then | |||
0 | |||
elseif w< epsilon then | |||
(w/epsilon+1)^2*epsilon/4 | |||
else | |||
w; | |||
plot2d(K(w,0.5),[w,-1,1], | |||
[ylabel,"K/(k*W)->"], [xlabel,"w/W->"], | |||
[legend, "restoring force, ε=0.5"]); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
[[Datei:Kw53-12.png|mini|Freikörperbild|alternativtext=|links|119x119px]]Die Gleichgewichtsbedingung lesen wir mit dem [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|Prinzip von d'Alembert]] aus dem Freikörperbild ab: | |||
::<math>- m\cdot\ddot{h} - m\cdot g + K(w) = 0</math> | |||
Mit der dimensionslosen Zeit und Höhe | |||
::<math>\tau = t/t_B</math>, | |||
::<math>\tilde{h} = h / r </math> | |||
sowie | |||
::<math>K = k \cdot r \cdot \tilde{K} </math> | |||
wird daraus | |||
::<math>\frac{\displaystyle m\cdot r}{\displaystyle {{t}_{B}^{2}}} \left( \displaystyle \frac{{{d}^{2}}}{d\,{{\tau}^{2}}}\cdot \tilde{h}\right) - k \cdot r \cdot \tilde{K} \left( -\tilde{h},\frac{1}{100}\right) +g\cdot m=0</math>. | |||
Weil wir ab hier mit den dimensionslosen Koordinaten weiterarbeiten, lassen wir die Tilde über dem ''h'' gleich wieder weg - so wird's übersichtlicher. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/********************************/ | |||
/* define ODE in dim'less coordinate h */ | |||
dgl : m*r/t[B]^2*'diff(h,t,2)-k*r*K(-h,1/100)+m*g = 0; | |||
dgl : expand(solve(dgl, 'diff(h,t,2)))[1]; | |||
dgl : expand(subst(params,dgl)); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text= | |||
Die Bewegungsgleichung zweiter Ordnung schrieben wir nun um als zwei Bewegungsgleichungen erster Ordnung zu | |||
::<math>\displaystyle \frac{d}{d\,\tau}\left(\begin{array}{c}h\\v\end{array}\right) = \underline{f}(h)</math>. | |||
Die rechte Seite der gewöhnlichen Differentialgleichung ("Right-hand-side of ODE") lautet damit | |||
::<math>\begin{pmatrix}v\\ 100.0\cdot \left( \text{ if } -1.0\cdot h<-0.01 \text{ then } 0.0 \text{ elseif } -1.0\cdot h<0.01 \text{ then } 0.5\cdot {{h}^{2}}-0.01\cdot h+5.0\cdot {{10}^{-5}} \mathrm{else} -1.0\cdot h\right) -1.0\end{pmatrix}</math> | |||
Und diese können wir - hier mit dem [[Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Runge-Kutta-Verfahren 4.ter Ordnung|Runge-Kutta-Verfahren 4.ter Ordnung]] - lösen. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/********************************/ | |||
/* numerical solution of IVP */ | |||
times : subst([t0 = 0, tmax = 10, dt = 0.01], | |||
[t, t0, tmax, dt]); | |||
dgl1stOrder : subst(params,[v,float(expand(rhs(dgl)))]); | |||
stateVabs : [h,v]; | |||
initiVals : [10,0]; | |||
ivs : rk(dgl1stOrder, stateVabs, initiVals, times)$ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
Wir tragen die Höhe ''h'' über der Zeit und ''h'' über ''v'' im [[Sources/Lexikon/Phasendiagramme|Phasendiagramm]] auf: | |||
Height ''h'':[[Datei:Kw53-13.png|mini|Lösung im Zeitbereich|alternativtext=|ohne]]Phase Diagram:[[Datei:Kw53-14.png|mini|Lösung im Phasenraum|alternativtext=|ohne]] | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/********************************/ | |||
/* plot time functions */ | |||
T : makelist(ivs[j][1],j,1,length(ivs))$ | |||
H : makelist(ivs[j][2],j,1,length(ivs))$ | |||
V : makelist(ivs[j][3],j,1,length(ivs))$ | |||
plot2d([discrete, T, H], | |||
[title, sconcat("start @: ",string(initiVals))], | |||
[xlabel,"τ/1->"], [ylabel,"h/1->"]); | |||
/* phase plot */ | |||
plot2d([discrete,H,V], [legend, false], [x,-1,10], | |||
[ylabel,"V/1->"], [xlabel,"H/1->"]); | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Aktuelle Version vom 27. März 2021, 07:47 Uhr
Aufgabenstellung
Eine Kugel (Masse m, Radius r) wird aus der Höhe H im Erdschwerefeld losgelassen, kommt auf den Boden auf und „springt“ dann wie ein Flummi auf und ab. Der Stoß zwischen Kugel und Oberfläche sei ideal-elastisch. Gefragt ist eine numerische Lösung des Problems als Anfangswertproblem.
Dabei modellieren Sie die Kugel als elastisch, die Unterlage als starr. Die Kugel können Sie sich so wie unten skizziert im unteren Teil durch eine Feder ersetzt denken.
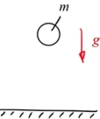
Eine elastische Kugel wird im Erdschwerefeld losgelassen und „springt“ wie ein Flummi auf und ab. Gesucht ist die numerische Lösung als Anfangswertproblem.
Lösung mit Maxima
Die Schwierigkeit kommt aus der Modellierung der Kontaktkraft zwischen Boden und Kugel. Oft reicht es, ein phänomenologisches Modell zu implementieren - also die Kontaktkraft als reine "Federkraft" zu interpretieren.
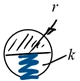
| Kugel-Modell: elastischer Kontakt mit Einfederung w. | |
|---|---|
 |
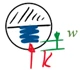 |
Die Federkraft K ist also Null, solange die Kugel die Oberfläche nicht berührt und sie sei hier - eine weitere drastische Vereinfachung - proportional zur Federkompression w, wenn sich Kugel und Oberfläche berühren:
Header
Wir lösen das Anfangswertproblem zu einer nichtlinearen Bewegungsgleichung. Die Nichtlinearität kommt aus der Kontaktbedingung der Kugel mit der Oberfläche.
Die Bewegungsgleichung ist stückweise linear, hier erfassen wir sie durch eine Kennlinie, die wir zwischen den linearen Bereich ausrunden. Das Ausrunden macht die numerische Integration schneller.
/*********************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-09-24 */
/* ref: Kw23 (TM-C, Labor 5) */
/* description: finds the solution for */
/* the nonlinear IVP */
/*********************************************************/
Declarations
Wir verwenden die Parameter
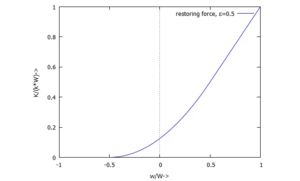
Die Kennlinie für den Kontakt definieren wir stückweise zu
Und so sieht sie dann aus:
/*********************************************************/
/* declarations */
assume(g>0, r>0);
/* parameter */
params: [k = kappa*m*g/r, /*spring stiffness*/
t[B] = sqrt(2*r/g), /*reference time*/
kappa = 100]; /*dim'less spring stiffness*/
/**** define nonlinear spring characteristic ***/
K(w,epsilon) := if w <- epsilon then
0
elseif w< epsilon then
(w/epsilon+1)^2*epsilon/4
else
w;
plot2d(K(w,0.5),[w,-1,1],
[ylabel,"K/(k*W)->"], [xlabel,"w/W->"],
[legend, "restoring force, ε=0.5"]);
Equilibrium Conditions
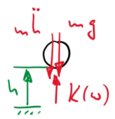
Die Gleichgewichtsbedingung lesen wir mit dem Prinzip von d'Alembert aus dem Freikörperbild ab:
Mit der dimensionslosen Zeit und Höhe
- ,
sowie
wird daraus
- .
Weil wir ab hier mit den dimensionslosen Koordinaten weiterarbeiten, lassen wir die Tilde über dem h gleich wieder weg - so wird's übersichtlicher.
/********************************/
/* define ODE in dim'less coordinate h */
dgl : m*r/t[B]^2*'diff(h,t,2)-k*r*K(-h,1/100)+m*g = 0;
dgl : expand(solve(dgl, 'diff(h,t,2)))[1];
dgl : expand(subst(params,dgl));
Solving
Die Bewegungsgleichung zweiter Ordnung schrieben wir nun um als zwei Bewegungsgleichungen erster Ordnung zu
- .
Die rechte Seite der gewöhnlichen Differentialgleichung ("Right-hand-side of ODE") lautet damit
Und diese können wir - hier mit dem Runge-Kutta-Verfahren 4.ter Ordnung - lösen.
/********************************/
/* numerical solution of IVP */
times : subst([t0 = 0, tmax = 10, dt = 0.01],
[t, t0, tmax, dt]);
dgl1stOrder : subst(params,[v,float(expand(rhs(dgl)))]);
stateVabs : [h,v];
initiVals : [10,0];
ivs : rk(dgl1stOrder, stateVabs, initiVals, times)$
Post-Processing
Wir tragen die Höhe h über der Zeit und h über v im Phasendiagramm auf:
Height h:
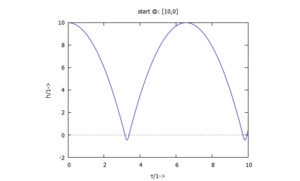
Phase Diagram:
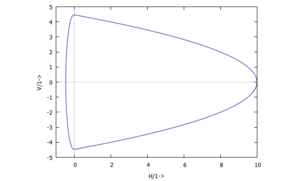
/********************************/
/* plot time functions */
T : makelist(ivs[j][1],j,1,length(ivs))$
H : makelist(ivs[j][2],j,1,length(ivs))$
V : makelist(ivs[j][3],j,1,length(ivs))$
plot2d([discrete, T, H],
[title, sconcat("start @: ",string(initiVals))],
[xlabel,"τ/1->"], [ylabel,"h/1->"]);
/* phase plot */
plot2d([discrete,H,V], [legend, false], [x,-1,10],
[ylabel,"V/1->"], [xlabel,"H/1->"]);
Links
- ...
Literature
- ...