Gelöste Aufgaben/Hko8: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
|||
| (6 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
<onlyinclude> | |||
[[Datei:Hko8-01.png|mini|left|Lageplan|alternativtext=|200x200px]] | |||
Drei Stäbe 1, 2 und 3 werden in Punkt A verbunden. Aufgrund einer Fertigungstoleranz ist Stab 3 um zu kurz. | |||
Gesucht ist die Verschiebung des Punktes ''A'' nach dem Einhängen von Stab 3 sowie die Spannungen in den Stäben.</onlyinclude> | |||
Die drei Stäbe haben die Querschnittsfächen | Die drei Stäbe haben die Querschnittsfächen | ||
| Zeile 21: | Zeile 25: | ||
Alle Stäbe sind aus dem gleichen Material mit E-Modul ''E'': | Alle Stäbe sind aus dem gleichen Material mit E-Modul ''E'': | ||
< | == Lösung mit Maxima == | ||
[[Datei: | ... nach dem Prinzip vom Minimum der potentiellen Energie: | ||
* "Das System ist im Gleichgewicht, wenn die Potentielle Energie des Systems ein Minimum hat." | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Wir arbeiten mit wxMaxima 15.08.2. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2017-02-28 */ | |||
/* ref: Mathe 2 */ | |||
/* description: Dehnstäbe verspannt eingebaut */ | |||
/* */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text=Parameter: | |||
::<math>a=\tan\left( \alpha\right) \cdot h,\alpha=\frac{\pi }{6},{{A}_{3}}={{A}_{1}},{{A}_{2}}=2\cdot {{A}_{1}}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
assume(a>0, h>0); | |||
par : [a = h*tan(alpha), alpha = %pi/6, A[3]=A[1], A[2]=2*A[1]]; | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Kinematics | |||
|text= | |||
[[Datei:Hk08-11.png|mini|Freischnitt: Knoten A|alternativtext=|205x205px]] | |||
Aus dem Satz des Pythagoras kommt: | |||
::<math>\begin{array}{lll}{{\left( {{\Delta}_{1}}+{{l}_{1}}\right) }^{2}}={{\left( h-v\right) }^{2}}+{{\left( a-u\right) }^{2}}\\ {{\left( {{\Delta}_{3}}+{{l}_{3}}\right) }^{2}}={{\left(h -\Delta-v\right) }^{2}}+{{u}^{2}}\\ {{\left( {{\Delta}_{2}}+{{l}_{2}}\right) }^{2}}={{\left( h-v\right) }^{2}}+{{\left( a+u\right) }^{2}}\end{array}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
length : [(l[1]+Delta[1])^2 = (h -v)^2+(a-u)^2, | |||
(l[3]+Delta[3])^2 = (h-elta-v)^2+( u)^2, | |||
(l[2]+Delta[2])^2 = (h -v)^2+(a+u)^2]; | |||
diff : makelist(Delta[i],i,1,3); | |||
null : append([u=0, v=0], makelist(Delta[i]=0,i,1,3)); | |||
length : subst(par,length); | |||
L[0] : subst(par,solve(subst(null,length), makelist(l[i],i,1,3)))[5]; | |||
L[1] : expand(subst(L[0],subst([delta=0],length))); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Linearize for small deflections | |||
|text= | |||
Die Stab-Längung linearisieren wir bezüglich der Koordinaten ''u, v'' und erhalten | |||
'''Dehnungen:''' | |||
::<math>\displaystyle {{\varepsilon}_{1}}=-\frac{\sqrt{3}\cdot \left( u+\sqrt{3}\cdot v\right) }{4\cdot h},{{\varepsilon}_{2}}=\frac{\sqrt{3}\cdot \left( u-\sqrt{3}\cdot v\right) }{4\cdot h},{{\varepsilon}_{3}}=\frac{-v+\Delta+\text{...}}{h-\Delta}</math> | |||
'''Spannungen''': | |||
::<math>\displaystyle {{\sigma}_{1}}=-\frac{\sqrt{3}\cdot \left( u+\sqrt{3}\cdot v\right) \cdot E}{4\cdot h},{{\sigma}_{2}}=\frac{\sqrt{3}\cdot \left( u-\sqrt{3}\cdot v\right) \cdot E}{4\cdot h},{{\sigma}_{3}}=\frac{\left( -v+\Delta+\text{...}\right) \cdot E}{h-\Delta}</math> | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
/* Linearisieren */ | |||
/* entweder .... */ | |||
L[2] : trunc(taylor(solve(L[1],diff),[u,v],0,1)[2]); | |||
/* oder .... */ | |||
small : [u,v,Delta[1],Delta[2],Delta[3], delta]; | |||
L[3] : solve(subst([nu=1],subst([nu^2=0], subst(makelist(small[i] = nu*small[i],i,1,length(small)),L[1]))),diff)[1]; | |||
Epsilon : subst(L[2],subst(L[0], makelist(epsilon[i] = Delta[i]/l[i],i,1,3))); | |||
Sigma : makelist(sigma[i] = subst(Epsilon,E*epsilon[i]),i,1,3); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text= | |||
''U'' hat ein Minimum (Extremwert), wenn | |||
::<math>\frac{\displaystyle dU}{\displaystyle du} \stackrel{!}{=} 0 \;\text{ und } \; \frac{\displaystyle dU}{\displaystyle dv} \stackrel{!}{=} 0</math> | |||
wobei die Potentielle Energie im System | |||
::<math>\displaystyle U = \sum_{i=1}^3 U_i \text{ mit } U_i = \int_{\ell_i} \frac{1}{2} \sigma_i \cdot \varepsilon_i dx</math> | |||
ist und damit | |||
::<math>\displaystyle U=\frac{\sqrt{3}\cdot {{A}_{1}}\cdot {{\left( u+\sqrt{3}\cdot v\right) }^{2}}\cdot E}{8\cdot h}+\frac{\sqrt{3}\cdot {{A}_{1}}\cdot {{\left( u-\sqrt{3}\cdot v\right) }^{2}}\cdot E}{4\cdot h}+\frac{{{A}_{1}}\cdot {{\left( -v+\Delta+\text{...}\right) }^{2}}\cdot E}{h}</math>. | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
U : sum(subst(par, A[i]*subst(Epsilon,subst(Sigma, subst(L[0],sigma[i]*epsilon[i]*l[i])))),i,1,3); | |||
U : subst([h-delta=h],U); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text= | |||
Auflösen des Gleichungssystems liefert: | |||
::<math>\begin{array}{l}\displaystyle u=-\frac{\sqrt{3}-3}{6}\cdot \Delta,\\ \displaystyle v=\frac{\sqrt{3}-1}{2}\cdot \Delta\end{array}</math> | |||
Die Stab-Kräfte erhalten wir entsprechend zu | |||
== | ::<math>\begin{array}{l}\displaystyle {{S}_{1}}=-\frac{\left( \sqrt{3}-1\right) \cdot {{A}_{1}}\cdot E}{2\cdot h}\cdot \Delta,\\\displaystyle {{S}_{2}}=-\frac{\left( \sqrt{3}-1\right) \cdot {{A}_{1}}\cdot E}{2\cdot h}\cdot \Delta,\\\displaystyle {{S}_{3}}=-\frac{\left( \sqrt{3}-3\right) \cdot {{A}_{1}}\cdot E}{2\cdot h}\cdot \Delta\end{array}</math>. | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/*******************************************************/ | |||
sol[1] : solve([diff(U,u) = 0, diff(U,v) = 0],[u,v])[1]; | |||
sol[2] : ratsimp(subst([h-delta=h],subst(sol[1],makelist(S[i] = subst(par,subst(Sigma,A[i]*sigma[i])),i,1,3)))); | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Post-Processing | ||
|text= | |text=[[Datei:Hk08-12.png|mini|Potential '''''U'''(u,v).'']] | ||
Das Potential können wir über ''u,v'' plotten - die Gleichgewichtsbeziehung ist im Minimum der Fläche. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | |||
/*******************************************************/ | |||
/* plots */ | |||
Upsilon: ratsimp(subst([gamma = 1/100], subst([u=alpha*h,v=beta*h, delta = gamma*h],U)/(E*A[1]*h))); | |||
plot3d(Upsilon,[alpha,-1/10,1/10],[beta,-1/10,1/10]) | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
'''Links''' | '''Links''' | ||
| Zeile 43: | Zeile 172: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Aktuelle Version vom 9. März 2021, 11:53 Uhr
Aufgabenstellung
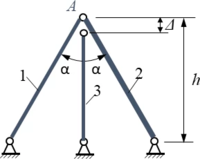
Drei Stäbe 1, 2 und 3 werden in Punkt A verbunden. Aufgrund einer Fertigungstoleranz ist Stab 3 um zu kurz. Gesucht ist die Verschiebung des Punktes A nach dem Einhängen von Stab 3 sowie die Spannungen in den Stäben. Die drei Stäbe haben die Querschnittsfächen
und die Abmessungen
Alle Stäbe sind aus dem gleichen Material mit E-Modul E:
Lösung mit Maxima
... nach dem Prinzip vom Minimum der potentiellen Energie:
- "Das System ist im Gleichgewicht, wenn die Potentielle Energie des Systems ein Minimum hat."
Header
Wir arbeiten mit wxMaxima 15.08.2.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-02-28 */
/* ref: Mathe 2 */
/* description: Dehnstäbe verspannt eingebaut */
/* */
/*******************************************************/
Declarations
Parameter:
/*******************************************************/
assume(a>0, h>0);
par : [a = h*tan(alpha), alpha = %pi/6, A[3]=A[1], A[2]=2*A[1]];
Kinematics
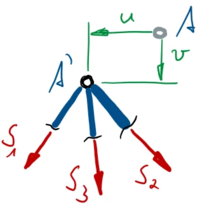
Aus dem Satz des Pythagoras kommt:
/*******************************************************/
length : [(l[1]+Delta[1])^2 = (h -v)^2+(a-u)^2,
(l[3]+Delta[3])^2 = (h-elta-v)^2+( u)^2,
(l[2]+Delta[2])^2 = (h -v)^2+(a+u)^2];
diff : makelist(Delta[i],i,1,3);
null : append([u=0, v=0], makelist(Delta[i]=0,i,1,3));
length : subst(par,length);
L[0] : subst(par,solve(subst(null,length), makelist(l[i],i,1,3)))[5];
L[1] : expand(subst(L[0],subst([delta=0],length)));
Linearize for small deflections
Die Stab-Längung linearisieren wir bezüglich der Koordinaten u, v und erhalten
Dehnungen:
Spannungen:
/*******************************************************/
/* Linearisieren */
/* entweder .... */
L[2] : trunc(taylor(solve(L[1],diff),[u,v],0,1)[2]);
/* oder .... */
small : [u,v,Delta[1],Delta[2],Delta[3], delta];
L[3] : solve(subst([nu=1],subst([nu^2=0], subst(makelist(small[i] = nu*small[i],i,1,length(small)),L[1]))),diff)[1];
Epsilon : subst(L[2],subst(L[0], makelist(epsilon[i] = Delta[i]/l[i],i,1,3)));
Sigma : makelist(sigma[i] = subst(Epsilon,E*epsilon[i]),i,1,3);
Equilibrium Conditions
U hat ein Minimum (Extremwert), wenn
wobei die Potentielle Energie im System
ist und damit
- .
/*******************************************************/
U : sum(subst(par, A[i]*subst(Epsilon,subst(Sigma, subst(L[0],sigma[i]*epsilon[i]*l[i])))),i,1,3);
U : subst([h-delta=h],U);
Solving
Auflösen des Gleichungssystems liefert:
Die Stab-Kräfte erhalten wir entsprechend zu
- .
/*******************************************************/
sol[1] : solve([diff(U,u) = 0, diff(U,v) = 0],[u,v])[1];
sol[2] : ratsimp(subst([h-delta=h],subst(sol[1],makelist(S[i] = subst(par,subst(Sigma,A[i]*sigma[i])),i,1,3))));
Post-Processing
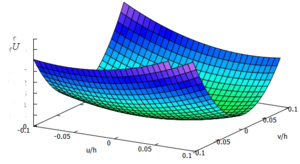
Das Potential können wir über u,v plotten - die Gleichgewichtsbeziehung ist im Minimum der Fläche.
/*******************************************************/
/* plots */
Upsilon: ratsimp(subst([gamma = 1/100], subst([u=alpha*h,v=beta*h, delta = gamma*h],U)/(E*A[1]*h)));
plot3d(Upsilon,[alpha,-1/10,1/10],[beta,-1/10,1/10])
Links
- ...
Literature
- ...